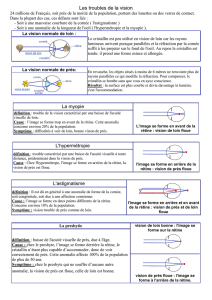
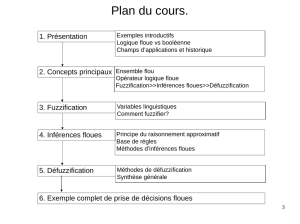
La logique floue

!
!"#$%&'()*"&'
"#$%&'()

*
+,-./'0$12,'0$3$4256$-767&52
"68&,9'(8.,6
:,';<06;0=>20;$?2,';$@:A1B
CD7&58.,6;$;'&$:A1
E0258.,6;$?2,'0;F$G5&.5>20;$2.6-'.;8./'0;F$D&,D,;.8.,6;$
?2,'0;
E5.;,660=068$?2,'
H0&;$25$I,==5690$?2,'0

J
+,-./'0$12,'0$3$K.>2.,-&5DL.0
La#logique#floue#et#ses#applicationsF$K#$K,'(L,6<
M0'6.0&F$N99.;,6$O0;20P$79#F$!QQR
La#logique#floueF$K#$K,'(L,6<M0'6.0&F$S'0<;5.;<T0U$
4V1#
The#Fuzzy#Future#:#From#Society#and#Science#to#
Heaven#in#a#ChipF$K5&8$W,;),F$X5&=,6P$K,,);#
An#Introduction#to#Fuzzy#Sets:#Analysis#and#DesignF$
O#$409&P(Y$Z$1#$[,=.90F$M.8$4&0;;$79#

\
+,-./'0$12,'0$3$"68&,9'(8.,6
X.;8,&./'0
]70$06$!Q^R$@+,8?.$_590LF$K0&)020PB
560(9,80$3$(&7605'$06$G,.8'&0
D,'&$_590LF$;.='20&$9,6($modéliser#le#comportement#
humain 67(0;;.803
-0;8.,6$90;$5DD&,`.=58.,6;
0`D7&.06(0
!"#$%&' ?2,'0$.=D2./'0$90;$&a-20;$D,'&$,>806.&$90;$
979'(8.,6;#
A`$90$&a-20$'8.2.;70$/',8.9.0660=068$.=D2.(.80=0683
si ?0'$&,'-0$08$si G.80;;0bG7L.('20$720G70$08$si ?0'$D&,(L0$
alors ?&0.65-0$?,&8

R
+,-./'0$12,'0$3$"68&,9'(8.,6$
%&56;D,;.8.,6$90$(0880$&a-20$;56;$'8.2.;0&$20$?2,'3
Si ?0'$&,'-0$08$si G.80;;0bG7L.('20$97D5;;0$\cFJ$)=dL$08$si
?0'$0;8$e$=,.6;$90$RRFf$=a8&0;$alors ?&0.60&$5G0($'60$?,&(0$
90$*cFQ$60g8,6;$hh
ij$+1$?,&=52.;0$20$=,690$06$5DD&7(.568$90$?5k,6$
5DD&,`.=58.G0$20;$variables#d'entrées @?5.>20F$720G70F$
2,.6F$D&,(L0###B$08$de#sorties @?&0.65-0$27-0&$,'$?,&8B$08$
+1$79.(80$'6$06;0=>20$90$&a-20;$D0&=088568$90$
9780&=.60&$20;$;,&8.0;$06$?,6(8.,6$90;$068&70;#