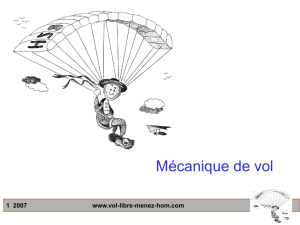
Modelisation 2D d`un kite pour production d`electricite

Problème : Modélisation simplifiée (à 2 dimensions) d’une éolienne par aile de kite. Optimisation de la
vitesse de déroulement du câble pour maximiser l’énergie produite.
(Thème : calcul algébrique, dérivation, équation du 2nd degré, optimum d’une fonction, étude de l’influence
de paramètres avec GeoGebra)
On considère un repère orthonormé {
i
,
j
,
k
} :
k
pointe verticalement vers le ciel.
Le vent souffle horizontalement à la vitesse w dans la direction de
i
Le kite vole à vitesse constante vk dans la direction de
j
et à altitude constante.
La force aérodynamique dans la direction de
i
est toujours compensée par le câble.
Ce câble, horizontal, est toujours parallèle à
i
lorsqu’il se déroule à la vitesse x.
www.skysails.de
câble de longueur r
et de tension FC
k
i
vent (wind)
kite
vue de face :
câble de longueur r et de tension
FC, se déroulant à la vitesse x
j
i
vent (wind)
kite
vue de dessus :
vk
j
(w – x)
i
e
w
L
F
D
F
w
i
γ
γ
i
k
j
1

La force de portance
L
F
et la force de traînée
D
F
sont dans le plan horizontal (
i
,
j
).
Du fait de son mouvement à la vitesse vk (généralement très élevée, avoisinant 80 m.s-1 soit 288 km.h-1),
l’aile de kite « voit » une vitesse relative de vent
e
w
égale à la somme vectorielle de (w - x)
i
et - vk
j
:
e
w
= (w - x)
i
- vk
j
.
En négligeant le poids du kite et du câble, les forces aérodynamiques s’exerçant sur le kite sont :
- la force de portance (aerodynamic Lift)
L
F
de norme FL =
2
1
ρair CL A we², qui tire sur l’aile et le câble par
effet Venturi (dépression sur le dessus de l’aile), où CL est le coefficient de portance de l’aile (et du câble), A
est la surface de l’aile de kite et ρair la masse volumique de l’air (on prendra ρair = 1,225 kg.m-3).
- la force de traînée (aerodynamic Drag)
D
F
de norme FD =
2
1
ρair CD A we², qui freine le déplacement de
l’aile, où CD est le coefficient de traînée de l’aile (et du câble), A est la surface de l’aile de kite et ρair la
masse volumique de l’air.
On a
L
F
⊥
D
F
et lors d’un vol stable,
L
F
+
D
F
=
c
F
est dans la direction du câble.
1) Exprimez tan γ en fonction de FD et FL.
En déduire que tan γ =
G
1
où le nombre G =
D
L
C
C
, rapport de la force de portance et de la force de traînée,
désigne la finesse de l’aile.
Pour les ailes de sport (kite surf, snow kite, …), la finesse G est comprise entre 2 et 8.
2) Exprimez tan γ en fonction de (w - x) et vk. En déduire que vk = G.(w - x)
Si x = 0 (le câble ne se déroule pas), la vitesse de l’aile de kite ne dépend donc que de sa finesse G et de la
vitesse du vent w.
3) Expression de l’effort exercé par l’aile :
On admet la relation
γ cos
1
=
γ ²tan
1+
.
a) Démontrer que Fc = FL
γ cos
1
.
En utilisant vk = G.(w - x), démontrer que :
we² = (w - x)² + G² (w - x) ² = (1 + G²) (w - x)²
puis que Fc =
2
1
ρair CL A (1 + G²)
²
1
1G
+
(w - x)².
Comme G ≥ 8, dire pourquoi on peut approximer Fc par Fc =
2
1
ρair CL A G² w².
Si x = 0 (le câble reste à longueur constante), la force Fc exercée par l’aile de kite sur le câble est donc
proportionnelle au carré de la vitesse du vent, et dépend du carré de la finesses G² de l’aile.
La finesse G est donc un paramètre important dans la conception d’une aile.
Pour les ailes de sport (kite surf, snow kite, …), la finesse G est comprise entre 2 et 8.
Pour les ailes d’avions, la finesse G est bien plus élevée et il semble possible de construire des ailes de kites
de haute finesse. La raison principale pour laquelle les ailes sportives de kite n’ont pas une finesse plus
élevée réside dans la relation vk = G.w avec x = 0 (: le kite aurait une vitesse vk trop élevée et difficile à
vent (wind)
kite
L
F
D
F
γ
c
F
i
j
2

contrôler) et dans la dernière expression de Fc (Fc serait trop grande d’où un grand danger pour le kite surfer,
comme le démontreront les calculs en fin de problème). En outre, la stabilité de l’aile diminue si sa finesse
augmente.
4) Maximisation de la puissance de l’aile :
Nous souhaitons ici maximiser la puissance P de l’aile de kite en vue de produire de l’énergie électrique
grâce à un alternateur entraîné par le déroulement du câble. Nous pouvons pour cela agir sur la vitesse de
déroulement (ou de sortie) du câble x.
Cette puissance P est donnée par P = force × vitesse
donc P = Fc x =
2
1
ρair CL A (1 + G²)
²
1
1G +
(w - x)² x
Comme G ≥ 8, on peut approximer P par P = Fc x =
2
1
ρair CL A G² (w - x)² x
Pour une aile donnée, avec une vitesse de vent donnée, ρair CL A G² est une constante, de même que w. La
puissance P ne dépend donc que de x.
a) On considère que le vent souffle à w = 12 m.s-1. Déterminez l’expression de la fonction P’, dérivée de la
fonction P définie par P(x) =
2
1
ρair CL A G² (w - x)² x.
En déduire le tableau de variation de la fonction P pour x ∈ [0 ; 12].
Déterminez pour quelle(s) valeurs de x la puissance P est maximale.
b) Reprendre la question précédente avec un vent soufflant à w = 15 m.s-1.
c) Quelle relation semble vérifier x et w lorsque la puissance est maximale ?
d) Sur un fichier GeoGebra, créer :
- un curseur A allant de 0 à 1000 m² avec un incrément de 50 m²
- un curseur G allant de 0 à 90 avec un incrément de 2
- un curseur w, allant de 0 à 50 avec un incrément de 1
- un curseur CL, allant de 1 à 2 avec un incrément de 0.1
Dans le logiciel GeoGebra, tapez P(x) =
2
1
*1,225*CL*A*G^2*(w-x)^2*x qui permet de tracer la
représentation graphique de la puissance P en fonction de la vitesse x de déroulement du fil.
Réglez les paramètres du graphique afin de représenter P pour x ∈ [0 ; w].
c) En modifiant les curseurs A et w, indiquer quelle relation semble vérifier x et w lorsque la puissance est
maximale.
Il est possible de tracer une famille de courbes avec GéoGebra en double-cliquant sur la courbe, puis en
choisissant « Propriétés » puis « Basique », et en cochant « Afficher la trace ».
Il est alors possible d’effacer toutes les courbes avec « Affichage » (en haut de l’écran) puis « Rafraîchir
l’affichage ».
d) Donner l’expression de la puissance maximale Pmaxi.
Que peut-on dire de cette puissance maximale et du cube de la vitesse du vent ?
3

Remarque : A titre de comparaison, B. Houska et M. Diehl prévoient avec une modélisation en 3D dans ces
conditions (une aile de 500 m² sous un vent à 12 m/s) une vitesse moyenne optimale de sortie du fil
d’environ 4,0 m/s (également) et une puissance moyenne de 6 MW (lors de la phase de traction) en prenant
en compte la traînée parasite de 1300 m de fil (de diamètre 6,7 cm et de masse 6630 kg). Ils prévoient 8,5
MW (lors de la phase de traction) dans une configuration en « dancing kites » avec 380 m de fil au-delà du
fil principal, essentiellement grâce à la réduction de la traînée parasite des fils.
Bibliographie :
- M. Diehl. Modelling and Optimal Control of Tethered Airfoils for Wind Power Generation, Optimization
in Engineering Center (OPTEC) & ESAT, K.U. Leuven, Belgium, 2009.
- B. Houska. Robustness and Stability Optimization of Open-Loop Controlled Power Generating Kites,
Universität Heidelberg, 2007.
- B. Lansdorp, B. Remes and W.J. Ockels. Design and testing of a remotely controlled surfkite for the
laddermill. In World Wind Energy Conference, Melbourne, 2005.
- M.L. Loyd. Crosswind Kite Power. Lawrence Livermore National Laboratory, California, 1980.
Correction
1) Dans le triangle rectangle formé par
L
F
et
D
F
, on a tan γ =
L
D
F
F
=
L
D
C
C
=
G
1
.
2) tan γ =
k
v
xw −
et donc
k
v
xw −
=
G
1
donc vk = G. (w - x).
3) a)
γ ²cos
1
=
γ
γγ
²cos
²sin²cos +
=
γ
γ
γ
γ
²cos
²sin
²cos
²cos +
= 1 +
)²
cos
sin
(
γ
γ
= 1 + tan²γ donc
γ cos
1
=
γ ²
tan1+
b) Fc = FL
γ cos
1
car cos γ =
c
F
FL
vk = G (w - x) et we² = (w - x)² + vk² d’après le théorème de Pythagore
donc we² = (w - x)² + G² (w - x) ² = (1 + G²) (w - x)²
On a alors Fc =
2
1
ρair CL A we²
γ cos
1
=
2
1
ρair CL A we²
γ
²tan1+
=
2
1
ρair CL A (1 + G²)
²
1
1G +
(w - x)²
que l’on peut approximer par Fc =
2
1
ρair CL A G² (w - x)²
c) Sous un vent à 12 m/s, Fc =
2
1
× 1,225 × 1,5 × 1,2 × 10²× (12 - 0)² ≈ 15 876 N ou 1588 daN (équivalent au
poids d’un objet de 1588 kg).
Sous un vent à 25 m/s, Fc =
2
1
× 1,225 × 1,5 × 1,2 (1 + 10²)
²10
1
1+
(25 - 0)² ≈ 68 906 N ou 6891 daN
(équivalent au poids d’un objet d’environ 7 tonnes).
4

4) a) P(x) =
2
1
ρair CL A (1 + G²)
²
1
1G +
(w - x)² x =
2
1
ρair CL A (1 + G²)
²
1
1G +
(w² - 2 wx + x²) x
=
2
1
ρair CL A (1 + G²)
²
1
1G +
(w² x - 2 w x² + x3)
donc la dérivée de P est définie par P’(x) =
2
1
ρair CL A (1 + G²)
²
1
1G +
(w² - 4 w x + 3x²)
P’(x) = 0 ⇔ (w² - 4 w x + 3 x²) = 0 car
2
1
ρair CL A (1 + G²)
²
1
1G +
est une constante > 0
3x²- 4 w x + w² = 0 la variable étant bien x (et non w)
∆ = 4 w² donc l’équation possède 2 solutions réelles qui sont
x1 =
6
24 ww +
= w et x2 =
6
24 ww −
=
3
w
P’(x) est du signe de a (= 3) à l’extérieur de ces racines
et du signe opposé à celui de a entre les racines
x
0
3
w
w
P’(x)
+ 0 - 0
P(x)
0 0
La puissance P(x) fournie par le kite à l’alternateur est donc maximale pour x =
3
w
, c'est-à-dire pour une
vitesse de « sortie » du câble égale au tiers de la vitesse du vent.
Cette puissance maximale est Pmaxi =
2
1
ρair CL A (1 + G²)
²
1
1G
+
(w²
3
w
- 2 w (
3
w
)² + (
3
w
)3)
Pmaxi =
2
1
ρair CL A (1 + G²)
²
1
1G +
(
3
3
w
-
9
3
2w
+
27
3
w
) =
2
1
ρair CL A (1 + G²)
²
1
1G +
(
27
9
3
w
-
27
3
6w
+
27
3
w
)
P
maxi
vitesse du vent
w en m/s
Force de traction F
c
en N
5