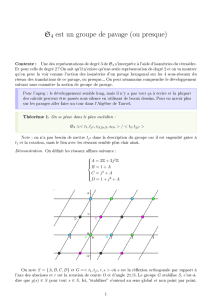
Tiling a Polygon with Parallelograms

Tiling a Polygon with Parallelograms
Richard Kenyon
rapport par Yassine Hamoudi
7 janvier 2016
Table des matières
1 Introduction 1
2 Contexte et état de l’art 2
3 Algorithme de pavage par des parallélogrammes 2
3.1 Recherche d’une correspondance valide . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
3.2 Correspondance à périphérie monotone et construction d’un pavage . . . . . . . . . . . . . 3
4 Autres résultats 4
4.1 Ensemble des pavages possibles et rotations . . . . . . . . . . . . . . . . . . . . . . . . . . 4
4.2 Définition alternative d’un "pavage" . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
4.3 NP-complétude.......................................... 5
5 Conclusion 5
Références 5
1 Introduction
Nous présentons le travail exposé dans [Ken93], concernant le pavage d’un polygone par des parallé-
logrammes. L’auteur s’intéresse au problème suivant :
Problème 1. Soit Pun polygone simple (i.e. qui ne s’intersecte pas avec lui-même). Existe-t-il un pavage
de Ppar un ensemble de parallélogrammes {Ti}tel que :
1. STirecouvre la région délimitée par P
2. deux tuiles Tiet Tjne peuvent s’intersecter que via un point ou une arête entière en commun
3. chaque tuile Tine peut intersecter Pque via un sommet ou une arête entière en commun.
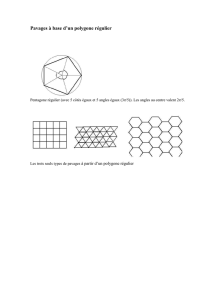
Figure 1 – Le pavage de gauche ne respecte pas les conditions 2 et 3 du problème (par exemple, l’arête
en gras n’intersecte qu’à moitié l’arête supérieure). Le pavage de droite est correct.
R. Kenyon propose un algorithme qui résout ce problème en temps quadratique, et construit un pavage
valide le cas échéant. Il démontre également que tous les pavages possibles sont équivalents à rotations
près. Enfin, différents résultats de NP-complétude sont établis (pavage par des polygones, des triangles
ou des trapèzes ; pavage d’une zone comportant un trou).
1

2 Contexte et état de l’art
Notons tout d’abord que le travail mené dans [Ken93] est très similaire à celui présenté dans [KS92].
L’algorithme développé dans ce dernier est cependant conçu pour une version légèrement différente du
Problème 1. Nous comparerons les deux approches dans la suite du rapport.
Plusieurs résultats de calculabilité existent concernant le pavage d’un plan infini. Berger prouva par
exemple dans [Ber66] que ce problème est indécidable pour un ensemble fini de tuiles. Une preuve alter-
native de ce résultat, issue de [Rob71], peut être adaptée au cas de la recherche d’un pavage périodique.
Concernant le pavage d’une région polygonale (éventuellement trouée), les problématiques abordées
concernent la NP-complétude, la recherche d’un pavage minimal (i.e. utilisant le moins de tuiles possible)
et le développement d’algorithmes de pavage efficaces. Le pavage d’une surface polygonale par un ensemble
fini prédéterminé de tuiles est NP-complet ([GJ79]). Ce n’est cependant plus le cas pour certaines variantes
de ce problème, notamment lorsqu’une infinité de tuiles différentes est disponible. B. Chazelle propose par
exemple un algorithme linéaire ([Cha91]) pour trianguler n’importe quel polygone simple. Des algorithmes
quadratiques existent aussi pour les trapézoïdes ou les rectangles horizontaux, voir respectivement [AAI86]
et [KK92]. L’article étudié ici obtient un résultat identique pour les parallélogrammes.
Il est intéressant de constater que le pavage d’une région polygonale trouée redevient un problème
NP-complet dans la plupart des cas précédents. Ceci a par exemple été démontré pour les trapézoïdes
([AAI86]) et les rectangles ([J.M91]). Nous verrons que c’est également le cas pour les parallélogrammes.
Enfin, le pavage d’une surface finie par des polygones élémentaires (triangles, losanges...) connaît une
utilité pratique en traitement de l’image et en modélisation par exemple.
3 Algorithme de pavage par des parallélogrammes
Nous présentons sommairement l’algorithme exposé dans [Ken93].
3.1 Recherche d’une correspondance valide
L’idée principale des algorithmes détaillés dans [Ken93] et [KS92] est de constater que tout pavage
d’une surface polygonale implique un appariement naturel entre arêtes de P. En effet, partant d’un arête
quelconque ede P, il existe une (unique) chaîne de parallélogrammes adjacents, qui ont tous deux côtés
identiques à eet qui rejoignent une autre arête e0située sur un bord opposé.
Figure 2 – En gras, la chaîne de parallélogrammes qui apparie eet e0.
On oriente dorénavant Pdans le sens antihoraire. Un appariement est ainsi une paire (e, e0)telle que
eet e0ont même longueur, même direction, et sont de sens opposés. Une correspondance est un ensemble
d’appariements disjoints contenant toutes les arêtes de P. Il est facile de constater que tout pavage correct
de Pimplique une correspondance particulière (obtenue en suivant les chaînes de parallélogrammes).
On dit également que deux paires (e1, e0
1)et (e2, e0 2)d’une correspondance se croisent s’il n’est pas
possible de tracer deux chemins (dans la surface polygonale) qui relient e1àe0
1, et e2àe0 2, sans s’intersecter.
Figure 3 – Correspondance entre arêtes. Les paires (e1, e0
1)et (e2, e0 2)se croisent.
2

L’objectif est de déterminer l’ensemble de propriétés que doit vérifier une correspondance pour qu’il
existe un pavage qui la réalise (i.e. les appariements impliqués par les chaînes de parallélogrammes
du pavage sont exactement ceux de la correspondance). Par exemple, s’il est possible de réaliser la
correspondance de la Figure 3, alors les deux chaînes de parallélogrammes associées aux paires (e1, e0
1)et
(e2, e0
2)devront forcément s’intersecter selon un parallélogramme [e1, e0 1, e2, e0 2](voir un exemple Figure
4). Cette observation sur les croisements permet d’établir plusieurs conditions nécessaires.
Figure 4 – Illustration d’un pavage qui réalise le croisement entre (e1, e0
1)et (e2, e0 2).
Définition 1. Une correspondance est valide si elle vérifie les deux conditions suivantes :
1. Pour toutes paires (e1, e0
1)et (e2, e0 2), si e1et e2ont même longueur et même direction alors les
deux couples ne se croisent pas.
2. Pour toute paire (e, e0), il existe un chemin "croissant" (dans la surface polygonale) qui relie les
deux arêtes (i.e. eet e0peuvent se “voir” à l’intérieur de P).
Figure 5 – Deux exemples ne respectant pas respectivement les conditions 1 et 2 de la Définition 1.
Toute correspondance impliquée par un pavage correct est valide. R. Kenyon démontre alors le résultat
suivant :
Proposition 2 (section 2.1 de [Ken93]).Tout polygone Padmet au plus une correspondance valide.
Éléments de preuve. La preuve présentée dans [Ken93] est constructive. On détermine d’abord l’ensemble
des paires qui se “voient” (cf condition 2 de la Définition 1), en construisant une triangulation de P
(algorithme linéaire de [Cha91] par exemple). Ensuite, la correspondance est obtenue en étudiant la
hauteur à laquelle chaque arête est placée dans le polygone.
3.2 Correspondance à périphérie monotone et construction d’un pavage
Lorsque deux paires (e1, e0
1)et (e2, e0 2)se croisent, avec e2entre e1et e0 1(Pparcouru dans le sens
antihoraire), on dit que le croisement est convexe si l’angle (orienté) entre e1et e2est inférieur à 180°:
Cette condition est rendue nécessaire par le fait que l’intersection entre deux chaînes reliant e1àe0
1
et e2àe0
2doit former un parallélogramme [e1, e2, e0 1, e0 2](cf Figure 4).
Définition 3. Une correspondance est à périphérie monotone si toutes ses paires croisées sont convexes.
3

La correspondance illustrée Figure 3 est à périphérie monotone. R. Kenyon déduit de cette caracté-
ristique la propriété suivante :
Proposition 4 (théorème 3 de [Ken93]).Padmet une correspondance à périphérie monotone si et
seulement s’il existe un pavage par des parallélogrammes qui réalise cette correspondance.
Éléments de preuve. Le sens inverse de la preuve est évident. Le sens direct s’obtient par une démonstra-
tion constructive. On considère une paire (e, e0)qui croise toutes les autres paires ayant une arête entre
eet e0(Pparcouru dans le sens antihoraire). On relie alors eet e0par une chaîne de parallélogrammes
adjacents aux arêtes situées entre eet e0, puis on appelle récursivement l’algorithme sur le reste de la
surface polygonale à paver.
Dans l’exemple de la correspondance à périphérie monotone de la Figure 3, le raisonnement précédent
peut s’appliquer à la paire (e2, e0
2). Cela conduit au placement d’une chaîne de parallélogrammes adjacents
aux arêtes inférieures du parallélogramme, illustré Figure 6 (à gauche). Une seconde étape de l’algorithme,
appliquée sur la sous-surface polygonale restante, conduit au pavage final (à droite, Figure 6).
Figure 6 – Exécution de l’algorithme de la Proposition 4 sur la correspondance de la Figure 3.
Toute correspondance à périphérie monotone étant aussi valide (puisqu’il existe un pavage correct
la réalisant), il existe donc au plus une correspondance à périphérie monotone possible (d’après la Pro-
position 2). Afin de paver une surface polygonale délimitée par P, il suffit donc de rechercher l’unique
correspondance valide potentielle (Proposition 2) puis d’essayer de la paver selon l’algorithme de la Pro-
position 4. L’algorithme global s’exécute en temps quadratique (cf section 2.1 de [Ken93]).
4 Autres résultats
Nous présentons brièvement les autres résultats détaillés dans [Ken93].
4.1 Ensemble des pavages possibles et rotations
Tout polygone admet au plus une correspondance à périphérie monotone (Proposition 4). Cependant,
il peut exister plusieurs pavages possibles comme en témoigne la Figure 7.
Figure 7 – Deux pavages corrects associés à la correspondance à périphérie monotone de la Figure 3.
Il est aisé de constater que tous les pavages possibles contiennent le même nombre de tuiles. En effet,
chaque tuile correspond exactement à l’intersection de deux chaînes de parallélogrammes associées à deux
paires (e1, e0
1)et (e2, e0 2)qui se croisent.
R. Kenyon démontre alors par récurrence sur le nombre de tuiles que tous les pavages possibles
s’obtiennent en effectuant des rotations autour des points intérieurs adjacents à trois parallélogrammes.
4.2 Définition alternative d’un "pavage"
[Ken93] et [KS92] présentent de grandes similarités dans leur travail. La plupart des concepts et
résultats précédemment énoncés sont communs aux deux articles (par exemple, la Proposition 4 et sa
4

preuve correspondent au théorème 1 de [KS92]). La preuve de la Proposition 2 se conclut toutefois
différemment dans [KS92], en résolvant un problème de flot dans un arbre.
Cependant, contrairement au Problème 1 étudié dans [Ken93], les auteurs de [KS92] autorisent les
intersections partielles entre arêtes (les deux exemples de la Figure 1 sont alors valides). Le travail présenté
dans [Ken93] peut toutefois s’adapter à ce cas. Il suffit en effet d’ajouter certains sommets au contour
de Ppour que les deux problèmes deviennent équivalents. Cela peut cependant conduire à obtenir n2
sommets (au lieu des ninitiaux), et donc une complexité en O(n4). Dans ce cas-là, il est plus intéressant
d’utiliser directement l’algorithme de [KS92] qui reste quadratique.
4.3 NP-complétude
Différents résultats de NP-complétude ont déjà été décrits Partie 2. R. Kenyon présente également un
corollaire direct à [GJ79] :
Corollaire 5. Soit Ωun ensemble de tuiles polygonales de surfaces supérieures à un, et comportant
chacune O(n)arêtes. Si Pest un polygone simple d’aire O(nk)et avec O(n)arêtes, alors paver Ppar
des tuiles de Ωest un problème NP-complet.
[Ken93] démontre que ce résultat persiste lorsque Ωcomporte uniquement des triangles, ou des trapé-
zoïdes. En effet, dans le premier cas on peut effectuer une réduction depuis le Corollaire 5 en découpant
chaque polygone en triangles qui devront forcément se réemboiter dans le pavage final. L’auteur réduit
ensuite ce résultat au deuxième cas, en découpant cette fois-ci chaque tuile triangulaire en trapézoïdes.
Par ailleurs, le Problème 1 devient NP-complet si le pavage comporte des trous. La preuve s’effectue
par réduction depuis le problème SUBSET-SUM. Elle consiste à placer un trou carré au centre d’un
polygone convexe bien choisi, afin que tout pavage valide contienne une chaîne depuis ce trou jusqu’à
une arête prédéterminée du bord. Les longueurs des parallélogrammes de cette chaîne constituent alors
la réponse à l’instance de SUBSET-SUM considérée.
5 Conclusion
Nous avons présenté dans ce rapport quelques résultats établis dans [Ken93] concernant le pavage
d’une région polygonale par des parallélogrammes. L’algorithme quadratique proposé par R. Kenyon a
notamment été esquissé.
Bien que l’on sache construire l’ensemble des pavages possibles (section 4.1), il ne semble pas exister
de manière de les dénombrer. Par ailleurs, il reste à trouver une caractérisation précise des types de tuiles
pour lesquels des algorithmes polynomiaux de pavage existent.
Références
[AAI86] Takao Asano, Tetsuo Asano, and Hiroshi Imai. Partitioning a polygonal region into trapezoids.
J. ACM, 33(2) :290–312, April 1986.
[Ber66] Robert Berger. The Undecidability of the Domino Problem. American Mathematical Society,
1966.
[Cha91] Bernard Chazelle. Triangulating a simple polygon in linear time. Discrete Comput. Geom.,
6(5) :485–524, August 1991.
[GJ79] Michael R. Garey and David S. Johnson. Computers and Intractability : A Guide to the Theory
of NP-Completeness. W. H. Freeman & Co., New York, NY, USA, 1979.
[J.M91] J.M.Robson. Sur le pavage de figures du plan par des barres. Actes des journées polyominos et
pavages, pages 95–103, 1991.
[Ken93] Richard Kenyon. Tiling a polygon with parallelograms. Algorithmica, 9(4) :382–397, 1993.
[KK92] Claire Kenyon and Richard Kenyon. Tiling a polygon with rectangles. In Proc. 33rd Symp.
Foundations of Computer Science, pages 610–619, 1992.
[KS92] Sampath Kannan and Danny Soroker. Tiling polygons with parallelograms. Discrete & Com-
putational Geometry, 7(2) :175–188, 1992.
[Rob71] RaphaelM. Robinson. Undecidability and nonperiodicity for tilings of the plane. Inventiones
mathematicae, 12(3) :177–209, 1971.
5