word

Semaine de la géométrie 29 mars au 2 avril 2004
Commission genevoise de l’enseignement des mathématiques (CEM) - 
Quelques éléments théoriques sur la notion de pavage
Définition
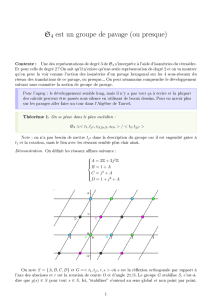
Un pavage du plan est une famille dénombrable de surfaces (sous-ensembles fermés du
plan){S1,S2,S3,...} qui recouvrent le plan tout entier et dont les intérieurs sont disjoints, ce qui
est équivalent au fait que les Si s'intersectent sur le bord (l'intérieur d'une surface Si étant Si
moins son bord). Le bord étant la ligne qui délimite la surface.
Remarque
Un pavage peut avoir une infinité de pièces différentes. Nous ne nous intéresserons qu'aux
pavages ayant un nombre fini de pièces différentes, l'ensemble des pavés, et surtout aux
pavages formés par un seul pavé.
Pavages périodiques
Parmi ces pavages certains sont périodiques, c'est-à-dire qu'il existe des isométries (autres
que l'identité) du plan qui préservent le pavage. C'est à ces pavages que nous allons nous
intéresser. On appelle le groupe du pavage l'ensemble des isométries du plan préservant le
pavage.
Rappelons qu'une isométrie du plan est une application f du plan dans lui-même qui préserve
les distances (i.e. Pour tout x et y dans le plan d(x,y)= d(f(x),f(y)) ) et que l'ensemble des
toutes ces applications forme un groupe pour la composition, notée fog(x)
et définie par fog(x)=f(g(x)).
Parmi toutes les isométries, certaines préservent le pavage, c'est-à-dire que l'image de tout Si
par l'application f est un Sj : f(Si)= Sj.
Dans le cas d'un pavage périodique, on appelle domaine fondamental du pavage (ou motif
minimal du pavage MERM[2]) un sous-ensemble du plan dont les images par le groupe du
pavage, redonnent le pavage de départ et tel que tout point du plan soit essentiellement dans
une et une seule image (le problème pouvant venir des points sur le bord du domaine
fondamental).
Techniquement si le domaine fondamental a un intérieur non vide, alors tout point de
l'intérieur a une unique image dans chacune des images du domaine fondamental.
Pour un pavage, il y a plusieurs domaines fondamentaux possibles.

Semaine de la géométrie 29 mars au 2 avril 2004
Commission genevoise de l’enseignement des mathématiques (CEM) - 
Il est important de noter que les notions de pavé et de domaine fondamental ne coïncident
pas toujours.
Si le pavage a un unique pavé, mais que le pavé a une (ou plusieurs) symétrie(s) alors un
domaine fondamental sera une partie du pavé qui le recouvre en utilisant cette (ou ces)
symétrie(s).
Exemple : Le pavage carré, dont un domaine fondamental est donné par un triangle rectangle
formé par le centre du carré, le milieu et l'extrémité d'un côté, voir en annexe pour le dessin.
Si le pavage a plusieurs pavés, alors un domaine fondamental contient au moins une partie de
chaque pavé, voir par exemple le pavage poisson oiseau d'Escher (voir plus loin).
Exemple : Dans [2], p.155, on montre comment rechercher ce domaine fondamental (voir
image deux pages plus loin)

Semaine de la géométrie 29 mars au 2 avril 2004
Commission genevoise de l’enseignement des mathématiques (CEM) - 
Remarque
Il existe des pavages non périodiques, exemple le pavage spiral p.22 [1].
Exemple de pavage non périodique à un seul pavé :
Quelques définitions et résultats pouvant être utiles dans certaines activités
Définitions
Un polygone est une suite finie de segments de droite (s1,...,sn) orientés tels que
la fin de si est le début de si+1 pour i allant de 1 à n-1 et la fin de sn est le début de s1.
C'est équivalent à la donnée d'une suite finie de points du plan (P1,...,Pn), les segments
si étant donné par [Pi,Pi+1] pour i allant de 1 à n-1 et sn étant donné par [Pn,P1].
Il est important de remarquer que l'ordre des Pi est important.
Les si s'appellent les arêtes et les Pi les sommets du polygone.

Semaine de la géométrie 29 mars au 2 avril 2004
Commission genevoise de l’enseignement des mathématiques (CEM) - 
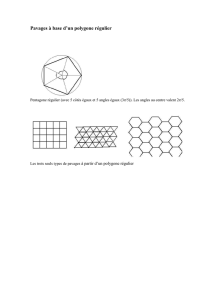
Un polygone régulier est une polygone convexe ayant tous les côtés et tous les angles au
sommet égaux (isométriques).
Un polygone est simple si ses arêtes ne s'intersectent qu'en ses sommets et que tous ses
sommets sont distincts.
Résultats
Les isométries du plan sont : les symétries axiales, les rotations, les translations et les
transsymétries (i.e. composition d'une symétrie axiale avec une translation parallèle à l'axe de
symétrie), les symétries centrales étant des rotations de 180°.
Le théorème des angles alternes-internes.
La somme des angles d'un triangle vaut 180 degrés.
La somme des angles d'un polygone à n côtés vaut (n-2) fois 180 degrés.
Eléments de bibliographie :
[1] Grunbaum and Shephard, Tilings and patterns, date?
[2] MERM : Chastellain, Calame, Brêchet, Mathématiques 7-8-9 Géométrie, 2003.
Pavage poissaux-oiseaux