Connaissances Capacités Commentaires 15.3 Symétrie axiale S

En Italique : Points du programme non exigibles pour le socle.
En italique, précédé d’un astérisque : item exigible pour le socle dans une classe ultérieure.
Connaissances Capacités Commentaires
3.2 Symétrie
orthogonale par
rapport à une droite
(symétrie axiale)
- Construire le symétrique d’un point, d’une droite,
d’un segment, d’un cercle (que l’axe de symétrie
coupe ou non la figure).
- Construire ou compléter la figure symétrique d'une
figure donnée ou de figures possédant un axe de
symétrie à l'aide de la règle (graduée ou non), de
l'équerre, du compas, * du rapporteur.
- Effectuer les tracés de l’image d’une figure par
symétrie axiale à l’aide des instruments usuels
(règle, équerre, compas).
L’élève peut utiliser la méthode de son
choix.
Dans la continuité du travail entrepris à
l'école élémentaire, les activités s'appuient
encore sur un travail expérimental (pliage,
papier calque) permettant d'obtenir un
inventaire abondant de figures simples, à
partir desquelles sont dégagées les
propriétés de « conservation » de la symétrie
axiale (conservation des distances, de
l'alignement, des
angles et des aires).
* Le rôle de la médiatrice comme axe de
symétrie d’un segment est mis en évidence.
15.3 Symétrie axiale
S Progression Nathan - transmath HACHETTE
Éducation 6è p 68+
1
=> Activités 1 et 2 sur feuille
1. SYMÉTRIQUE D’UNE FIGURE Oral p 228 : 14 - 18
App p 229 : 29 - (30) - 32 - 34
Ex p 67 : 3 - 4
Ex 2 - 3 - 4 - 5
(p 179+ : 37, 38, 39)
2
3
=> (Activité 3 sur feuille)
2. SYMÉTRIQUE D’UN POINT
A - Construction avec l'équerre et la règle
B - Construction avec le compas,
méthode de la médiatrice
C - Construction avec le compas,
méthode des 2 points
Oral p 228 : 19 - 20 - 21
App p 230 : ex 43 - (46) - 49
Ex p 68 : 1
Ex p 69 : 1 - 3
Ex p 70 : 3
Ex 8 - 9 - 10
(p 215+ : 43 à 47, 51,
52)
4
5
=> Activité 4 sur logiciel
3. PROPRIÉTÉS DE LA SYMÉTRIE AXIALE Oral p 228 : 15 - 22 - 23
App p 231 : ex 57 - (58)
(Ex p 74 : 4)
Ex p 68 : (2) - 5
Ex p 71*** : 3 - 4
(TAF p 73, ex 1 – 2 – 3
TAF p 74, ex 1 – 2)
Ex 12 - 13 - 14 - 15
Bilan p 176
=> Activités 3/4 p 169
p 179+ : 41, 45, 52,
53, 54, 56, 57, 58, 60,
68, 69, 71, 76
Bilan p 176 Les
curieux p 178
Les papillons : http://www.maths-et-tiques.fr/telech/PAPILLONS.pdf
Les poissons : http://www.maths-et-tiques.fr/telech/pavage_poisson.pdf

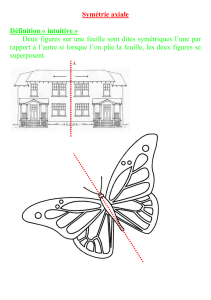
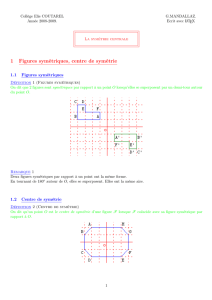
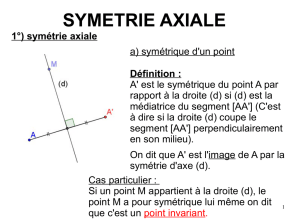
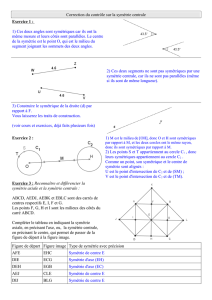
ACTIVITÉ 1 - MIROIR, MON BEAU MIROIR
Observe les trois figures ci-dessus.
Quel est leur point commun ?
Comment peux-tu le mettre en évidence ?
ACTIVITÉ 2 : LE SYMÉTRIQUE DANS L'ŒIL
Figure 1 Figure 2 Figure 3 Figure 4
Observe les figures ci-dessus. La figure bleue est-elle toujours symétrique
à la figure orange par rapport à la droite tracée ?
Justifie ta réponse en écrivant une phrase.
ACTIVITÉ 3 : SYMÉTRIQUE D'UNE DROITE
1 Avec TracenPoche ou Geogebra
a) Construis une droite (UV). Place deux points A et B puis un point M appartenant
à la droite (AB).
Construis le point M' symétrique de M par rapport à la droite (UV).
b) Déplace le point M et observe le point M'.
c) Demande la trace du point M' en utilisant le bouton. Déplace le point M et
observe la trace. Déduis-en la nature du symétrique d'une droite.
d) Construis le symétrique de la droite (AB) par rapport à l'axe (UV). Déplace les
points A et B, observe la position des droites et écris tes remarques.
2 Droite parallèle à l'axe
a) Trace deux droites parallèles (d) et (d1).
b) Construis la droite (d2) symétrique de (d1) par rapport à l'axe (d).
c) Que peux-tu dire des droites (d1) et (d2) ? Justifie ta réponse.
3 Droite perpendiculaire à l'axe
a) Construis deux droites (d) et (d1) perpendiculaires.
b) Place un point A sur la droite (d1) et construis son symétrique A' par rapport à
l'axe (d). Justifie la position du point A'.
c) Que peux-tu dire alors de la droite (d2) symétrique de la droite (d1) par rapport à
l'axe (d) ?
ACTIVITÉ 4 - PROPRIÉTÉS DE LA SYMÉTRIQUE AXIALE
1 Avec TracenPoche ou Geogebra
a) Construis un triangle ABC rectangle en A. On appelle I le milieu de [AC].
Trace le cercle (C) de diamètre [AC].
Trace une droite (BU).
On appelle A', B', C' et I' les symétriques respectifs de A, B, C et I par rapport à
l'axe (BU).
b) Quels sont le centre et le rayon du cercle (C') symétrique du cercle (C) par
rapport à la droite (BU) ? Justifie ta réponse.
c) Que remarques-tu pour le point B' ?
Que se passe-t-il lorsque l'axe de symétrie passe par le point I ? Comment
l'expliquer ?
d) Compare la mesure des angles des triangles ABC et A'B'C'. Tu pourras utiliser le
rapporteur.
2 Le point D est un point du cercle (C) de sorte que l'angle
^
CAD
mesure 35 °.
On appelle D' le symétrique du point D par rapport à l'axe (BU).
Sans construire D', Anis dit qu'il est possible de trouver la mesure de l'angle
^
C ' A' D'
Comment fait-il ?
3 Énonce les grandeurs qui sont conservées lors d'une symétrie axiale.
Figure 1 Figure 2 Figure 3

A - Construction avec l'équerre et la règle
On construit
la perpendiculaire à (d)
passant par le point P.
On reporte la distance
de P à (d) de l'autre côté
de (d) sur cette
perpendiculaire.
On obtient ainsi le point
S tel que (d) soit
la médiatrice de [PS].
B - Construction avec le compas, méthode de la médiatrice
On trace un arc de cercle
de centre P qui coupe
l'axe en deux points.
De l'autre côté de la droite
(d), on trace deux arcs de
cercle de même rayon et
de centre les deux points
précédents.
Ces deux arcs se coupent
en un point qui est le point
S, symétrique de P par
rapport à (d).
C - Construction avec le compas, méthode des 2 points
On prend deux points
distincts quelconques
M et N sur la droite (d).
On trace deux arcs de
cercle de centres les
deux points précédents
et passant par P.
Ces deux arcs
se coupent en un point
qui est le point S.
A - Construction avec l'équerre et la règle
On construit
la perpendiculaire à (d)
passant par le point P.
On reporte la distance
de P à (d) de l'autre côté
de (d) sur cette
perpendiculaire.
On obtient ainsi le point
S tel que (d) soit
la médiatrice de [PS].
B - Construction avec le compas, méthode de la médiatrice
On trace un arc de cercle
de centre P qui coupe
l'axe en deux points.
De l'autre côté de la droite
(d), on trace deux arcs de
cercle de même rayon et
de centre les deux points
précédents.
Ces deux arcs se coupent
en un point qui est le point
S, symétrique de P par
rapport à (d).
C - Construction avec le compas, méthode des 2 points
On prend deux points
distincts quelconques
M et N sur la droite (d).
On trace deux arcs de
cercle de centres les
deux points précédents
et passant par P.
Ces deux arcs
se coupent en un point
qui est le point S.
(d)
P
(d)
P
(d) (d)
P
(d) (d)
P
(d)
P
S
(d)
P
(d)
M
N
(d)
P
(d)
M
N
(d)
P
(d)
M
N
S
(d)
P
(d)
P
(d) (d)
P
(d) (d)
P
(d)
P
S
(d)
P
(d)
M
N
(d)
P
(d)
M
N
(d)
P
(d)
M
N
S
(d)
P
(d)
P
S
(d)
P
(d)
P
S

CHAPITRE 17
SYMÉTRIE AXIALE
Du grec, syn « avec » et metron « mesure ».
« symmetria » désignait la juste mesure.
1. SYMÉTRIQUE D’UNE FIGURE
Définitions
Deux figures sont symétriques par rapport à une droite si elles se superposent par pliage le
long de cette droite. Cette droite est appelée l'axe de symétrie.
Exemple
Les figures 1 et 2 se superposent par pliage le long de la droite (d) donc elles sont symétriques
par rapport à la droite (d).
On dit que la figure 1 est le symétrique de la figure 2 dans la symétrie axiale d'axe (d).
Ici, les points A et M sont symétriques par rapport à la droite (d).
A M
(d)