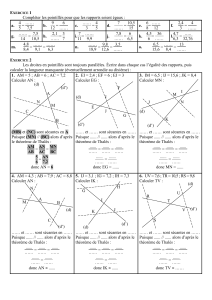
Correction du devoir maison N°1 Exercice 1 : a) n 0 1 2 3 4 5 6 7 8 9

Correction du devoir maison N°1
Exercice 1 :
a)
n0 1 2 3 4 5 6 7 8 9 10
f(n) 4 9 16 25 36 49 64 81 100 121 144
b) Il me semble que tous les nombres de la seconde ligne sont des carrés.
c) Pour tout entier naturel n, f(n) = (n + 4)n + 4 = n2 + 4n + 4 = (n + 2)2
Donc pour tout entier naturel n, l'image du nombre n par la fonction f est le carré de la somme de ce
nombre et de 2.
Exercice 2 :
A l'aide du patron, on peut en déduire que le chemin le plus court pour
aller de I en A est le segment [IA]. M est donc à l'intersection des segments
[IA] et [EF].
Comme ABFE est un carré, ses côtés opposés sont parallèles, (EF) et
(AB) sont alors parallèles. De plus (MA) et (BF) sont sécantes en I , on peut
alors appliquer le théorème de Thalès :
IF
IB
=MI
IA
=MF
AB
donc
3
7
=MF
4
soit MF
=12
7
Le point M est placé sur le segment [EF] à environ 1,7 cm de F.
Dans le triangle ABI rectangle en I, on peut appliquer le théorème de
Pythagore : AB2 + BI2 = AI2
AI2 =42+72= 16 + 49 = 65 soit AI =
√
65
La longueur du chemin est environ 8,1 cm.
Correction du devoir maison N°1
Exercice 1 :
a)
n0 1 2 3 4 5 6 7 8 9 10
f(n) 4 9 16 25 36 49 64 81 100 121 144
b) Il me semble que tous les nombres de la seconde ligne sont des carrés.
c) Pour tout entier naturel n, f(n) = (n + 4)n + 4 = n2 + 4n + 4 = (n + 2)2
Donc pour tout entier naturel n, l'image du nombre n par la fonction f est le carré de la somme de ce
nombre et de 2.
Exercice 2 :
A l'aide du patron, on peut en déduire que le chemin le plus court pour
aller de I en A est le segment [IA]. M est donc à l'intersection des segments
[IA] et [EF].
Comme ABFE est un carré, ses côtés opposés sont parallèles, (EF) et
(AB) sont alors parallèles. De plus (MA) et (BF) sont sécantes en I , on peut
alors appliquer le théorème de Thalès :
IF
IB
=MI
IA
=MF
AB
donc
3
7
=MF
4
soit MF
=12
7
Le point M est donc placé sur le segment [EF] à environ 1,7 cm de F.
Dans le triangle ABI rectangle en I, on peut appliquer le théorème de
Pythagore : AB2 + BI2 = AI2
AI2 =42+72= 16 + 49 = 65 soit AI =
√
65
La longueur du chemin est alors environ 8,1 cm.
I
F
BA
E
H
M
G
I
F
BA
E
H
M
G