Mécanique des fluides et thermochimie

Colles semaine 7, sujet A Langevin–Wallon, PT 2016-2017
Mécanique des fluides et thermochimie
Question de cours
Établir la relation de Bernoulli.
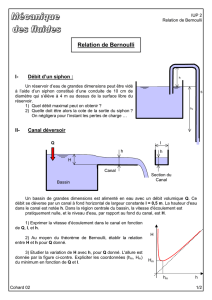
Exercice 1 : Écoulement de Poiseuille cylindrique
On considère l’écoulement d’un fluide visqueux dans une conduite cylindrique de rayon Ret longueur LR.
L’écoulement est induit par une différence de pression ∆Pimposée entre les deux extrémités de la conduite. En
coordonnées cylindriques d’axe zcorrespondant à l’axe de la conduite, le champ de vitesse est donné par
#”
v(r, θ, z) = −R2∆P
4η L 1−r2 R2#”
ez.
1 - Représenter sur un schéma les lignes de courant dans la conduite et le profil de vitesse dans une section droite
de la conduite.
2 - Vérifier que le profil de vitesse est compatibles avec les conditions aux limites.
3 - Cet écoulement est-il compressible ? Rotationnel ?
4 - Calculer le débit volumique au travers d’une section droite de la conduite.
Donnée : en coordonnées cylindriques et pour un champ vectoriel #” U,
div #” U=1
r
∂
∂r (rUr) + 1 r
∂Uθ
∂θ +∂ Uz ∂z
# ”
rot #” U=1
r
∂Uz
∂θ −∂ Uθ ∂z #”
er+∂Ur
∂z −∂ Uz ∂r #”
eθ+1
r∂ ∂r (rUθ)−∂Ur ∂θ #”
ez
Éléments de correction de l’exercice 1 :
1Lignes de courant sont des droites parallèles à #” ez. Le profil de vitesse est parabolique, maximal en r= 0 et nul
sur les bords de la conduite en r=R.
2Annulation de la vitesse sur les bords de la conduite, comme attendu pour un fluide visqueux.
3#” v=vz(r)#” ezdonc vzne dépend pas de zdonc div #” v= 0 donc écoulement incompressible. Pour le caractère
rotationnel, presque toutes les dérivées sont nulles, sauf
∂Uz
∂r =R2∆P 4η L ×2r R2=−∆P 2ηL r6= 0
L’écoulement est donc rotationnel, sauf le long de l’axe.
4Par définition, sur une section droite Sde normale #” ez
DV=¨S
#”
v·dS#” ez=R2∆P
4η L ¨S1−r2 R2rdrdθ=π∆P R4 16 η L
Exercice 2 : Cheminée au bioéthanol [oral CCP]
Les cheminées au bioéthanol constituent une alternative aux cheminées à bois traditionnelles. La combustion de
l’éthanol C2H5OH dans l’air produit des flammes d’une trentaine de centimètres de haut.
1 - Ecrire l’équation de combustion de l’éthanol. Les produits sont formés à l’état gazeux.
2 - Définir et calculer l’enthalpie standard de cette réaction, ∆rH◦.
3 - Calculer la masse d’air nécessaire à la combustion de 1,5 L d’éthanol.
4 - Déterminer la température de flamme Tfl, c’est-à-dire la température atteinte par le milieu réactionnel en négli-
geant tout transfert thermique avec l’extérieur. La température initiale vaut Ti= 298 K.
5 - En hiver, une pièce de 30 m2doit être chauffée avec une puissance P= 3 kW. Quel volume V0de bioéthanol
faudrait-il brûler par heure pour chauffer la pièce par ce seul moyen ? Commenter.
Données :
1/5 Étienne Thibierge, 10 novembre 2016, www.etienne-thibierge.fr

Colles semaine 7, sujet A : Mécanique des fluides et thermochimie Langevin–Wallon, PT 2016-2017
masses molaires (g ·mol−1) : H : 1,0 ; C : 12 ; N : 14 ; O : 16 ;
masse volumique, enthalpie standard de formation et capacité thermique molaire standard à pression constante (à
298 K) :
C2H5OH(liq) H2O(g) CO2(g) O2(g) N2(g)
ρ(kg ·m−3) 789 0,60 1,80 1,31 1,25
∆fH◦(kJ ·mol−1)−277,0 −241,8 −393,5 0 0
C◦
P(J ·K−1·mol−1) 111 33,6 37,1 29,4 29,1
Éléments de correction de l’exercice 2 :
1C2H5OH(liq) + 3 O2(g) = 2 CO2(g) + 3 H2O(g)
2Loi de Hess
∆rH◦= 2 ∆fH◦(CO2(g)) + 3 ∆fH◦(H2O(g))−3 ∆fH◦(O2(g))−∆fH◦(C2H5OH(liq)) = −1,24 ·103kJ ·mol−1.
3Quantité de matière contenue dans V= 1,5 L d’éthanol :
n=V×ρ
M=1,5·10−3×789
(24 + 6 + 16)10−3= 25,7 mol .
Quantité de matière minimale de dioxygène nécessaire : 3n.
Masse d’air nécessaire :
mair = 3nMO2+ 4 ×3nMO2= 11,1 kg
4On se place dans les conditions stœchiométriques et on raisonne en deux temps : d’abord la réaction à Ti= 298 K
puis le chauffage des produits de TiàTflsans oublier le diazote,
∆H=0=n∆rH◦+ [2nC◦
P(CO2)+3nC◦ P(H2O) + 4nC◦ P(N2)] (Tfl−Ti)
ce qui donne
Tfl=Ti−∆rH◦
2C◦
P(CO2)+3C◦ P(H2O) + 4C◦ P(N2)= 4,5·103K
C’est énorme !
5Transfert thermique cédé à la pièce par la réaction : Q=n∆rH◦, donc puissance de chauffage en ramenant à
un intervalle de temps ∆t:
P=Q
∆t=n∆rH◦ ∆t=V ρ ∆rH◦ M∆t
Ainsi
V=P M ∆t
ρ∆rH◦= 5 ·10−4m3= 0,5 L
Cela semble donc assez efficace.
2/5 Étienne Thibierge, 10 novembre 2016, www.etienne-thibierge.fr

Colles semaine 7, sujet B Langevin–Wallon, PT 2016-2017
Mécanique des fluides et thermochimie
Question de cours
Établir la relation de Bernoulli.
Exercice 1 : Alimentation en eau d’une maison depuis un château d’eau [banque PT 2015]
On s’intéresse à une alimentation domestique en eau via un château d’eau. Le château d’eau est modélisé par un
réservoir ouvert sur l’atmosphère, haut de H= 20 m et de section maximale S0= 25 m2, voir figure 1. Ce réservoir
débouche sur une canalisation horizontale de section s= 1,0·10−3m2. Cette canalisation alimente une installation
domestique qui comporte un robinet ouvrant sur l’air atmosphérique par une ouverture de même section s.
Figure 1
H
∆h
Figure 2
1 - Justifier que la vitesse d’écoulement de l’eau au niveau de la surface libre est négligeable devant la vitesse dans
la canalisation.
2 - Calculer numériquement le vitesse de l’eau en sortie du robinet en négligeant les pertes de charge.
3 - Calculer numériquement le débit volumique.
4 - Au niveau de la canalisation horizontale est le lieu d’une perte de charge régulière. Expliquer ce que cela signifie
et en donner les causes. Exprimer le théorème de Bernoulli en introduisant un coefficient Kcaractéristique de cette
perte de charge.
5 - Sur la canalisation horizontale on place deux tubes verticaux remplis d’eau séparés de 10 m. On mesure une
différence de hauteur d’eau ∆h= 2,0 cm, voir figure 2. En déduire la perte de charge linéaire due au tuyau d’alimen-
tation.
6 - Quelle est désormais la vitesse de l’eau en sortie du robinet situé à 1,0 km du chateau d’eau ?
7 - On souhaite retrouver la vitesse déterminée au début de l’exercice. On installe pour cela une pompe. Déterminer
la puissance qu’elle doit fournir.
Éléments de correction de l’exercice 1 :
1Écoulement suppose incompressible donc conservation du débit volumique donc
S0vlibre =svcan soit vlibre
vcan
=s
S0
1
2Bernoulli le long d’une ligne de courant qui va du haut du chateau d’eau jusqu’au robinet donne
P0+0+ρgH =P0+ρv2
sortie
2+ 0 d’où vsortie =pgH = 14 m ·s−1
3DV=vsorties= 14 ·10−3m3·s−1= 14 L ·s−1.
4Dissipation d’énergie mécanique par viscosité. Le théorème de Bernoulli devient
P0+0+ρgH =P0+ρv2
sortie
2+0+K
3/5 Étienne Thibierge, 10 novembre 2016, www.etienne-thibierge.fr

Colles semaine 7, sujet B : Mécanique des fluides et thermochimie Langevin–Wallon, PT 2016-2017
(ici Kest homogène à une pression, on peut le remplacer par ρgK0où K0est une hauteur, et on peut aussi introduire
une perte de charge linéaire homogène à une pression par unité de longueur)
5Relation de l’hydrostatique dans les prises de pression reliée à la pression dans la canalisation : Pcan =P0+ρgh.
Conservation du débit volumique indique que la vitesse d’écoulement est la même sous les deux prises de pression.
On en déduit
(P0+ρgh1) + ρv2
can
2+ρgzcan = (P0+ρgh2) + ρv2
can
2+ρgzcan +K
d’où
K=ρg∆hsoit k=K
L=ρ g ∆h L= 20 Pa ·m−1
6Bernoulli avec perte de charge kL0donne
P0+0+ρgH =P0+ρv2
sortie
2+0+kL0soit vsortie =s2gH −kL0 ρ= 13 m ·s−1
7kL0est l’énergie volumique perdue par perte de charge, qu’il faut donc compenser par une pompe de puissance
P=DVkL0.
Exercice 2 : Synthèse de l’acide fluorhydrique
L’acide fluorhydrique est obtenu industriellement par réaction du difluorure de calcium solide avec l’acide sulfu-
rique liquide pur. La réaction d’obtention de l’acide fluorhydrique peut s’écrire
CaF2(s) + H2SO4(liq) = 2 HF(g) + CaSO4(s) .
On introduit dans un four cylindrique (20 m de longueur et 3 m de diamètre) 220 kg de difluorure de calcium et
280 kg d’acide sulfurique, préalablement préchauffés à la température de 573 K sous 1 bar. Le four est maintenu à
cette même température par un chauffage externe. On admet que dans ces conditions la transformation est totale.
1 - Déterminer le transfert thermique reçu par les réactifs pour les chauffer de 298 K à 573 K.
2 - Calculer l’enthalpie standard de la réaction à 298 K. Dans la suite, on approximera la valeur de l’enthalpie
standard de réaction à 573 K à celle calculée à 298 K.
3 - Déterminer l’état final dans le réacteur (masse des solides et pression totale).
4 - Déterminer l’énergie thermique libérée par la réaction.
5 - Pourrait-on se passer de chauffage externe?
Données thermodynamiques :
Éléments de correction de l’exercice 2 :
1Chauffage à pression constante donc ∆H=Q=Cp∆T(premier principe pour phases condensées). Comme on
est à la pression standard on utilise directement les grandeurs standard,
Q=mCaF2
MCaF2
C◦
p,CaF2∆T+mH2SO4
MH2SO4
C◦
p,H2SO4∆T= 1,6·108J
4/5 Étienne Thibierge, 10 novembre 2016, www.etienne-thibierge.fr

Colles semaine 7, sujet B : Mécanique des fluides et thermochimie Langevin–Wallon, PT 2016-2017
Attention à tout justifier !
2Loi de Hess :
∆rH◦= 2∆fH◦(HF) + ∆fH◦(CaSO4)−∆fH◦(CaF2)−∆fH◦(H2SO4) = 69,8 kJ ·mol−1
La réaction est endothermique.
3Bilan de matière conduit à CaF2limitant, d’où à l’état final
nCaF2= 0
nH2SO4= 40 mol soit mH2SO4= 3,92 kg
nHF = 5,63 ·103mol
nCaSO4= 2,82 ·103mol soit mCaSO4= 383 kg
La pression finale se déduit de la loi des gaz parfaits,
p=4nHF R T
π d2= 1,9·105Pa .
4On parle de transfert thermique libéré et non pas à fournir, donc attention au signe : la réaction est endother-
mique, il faut donc fournir effectivement un transfert thermique.
Qr=−ξmax ∆rH◦=nCaF2∆rH◦=−1,97 ·108J
5Non : la réaction est endothermique.
5/5 Étienne Thibierge, 10 novembre 2016, www.etienne-thibierge.fr