TP1 – Découverte de Quartus II

TP1 – Découverte de Quartus II
Simon Rokicki
L'objectif de ce TP est de vous familiariser avec les outils qui seront utilisés au cours de ce semestre en
réalisant des circuits logiques très simples. Il est important de conserver tout fichier réalisé durant ce TP
car ceux-ci pourront être réutilisés plus tard.
Gestion des répertoires :


Pour des raisons pratiques, il est conseillé d'utiliser un répertoire et un projet différent pour
chaque exercice indépendant. Pour simplifier la création d'un projet, un modèle est donné (cf.
Utilisation des postes de travaux pratiques d'architectures des ordinateurs à l'aide de Quartus II).
Pour gérer votre bibliothèque personnelle de composants, il est conseillé de prévoir un dossier
spécial qui contiendra les fichiers .bdf et .bsf générés pendant les TP.
Exercice 1 : Utilisation de Quartus II
L’objectif de cet exercice et de réaliser votre premier circuit logique afin de prendre en main l’outil.
1. A l'aide du document annexe, réalisez un OU logique à deux entrées avec uniquement des portes
NON-ET à deux entrées (nand2 dans la catégorie combinatoire).
2. Reliez les entrées aux switchs (SW[1] et SW[0]) et la sortie à une LED (LEDG[0]).
3. Compilez et programmez la carte. Constatez le bon fonctionnement de la porte logique sur la
carte.
Exercice 2 : Multiplexeur
Un multiplexeur 1 bit permet de choisir entre deux entrées A et B à l’aide d’un bit de décision S. Si S vaut
0, la sortie du multiplexeur aura la même valeur que A. Si S vaut 1, la sortie aura la même valeur que B.
1. Réalisez le circuit d'un multiplexeur 1-bit.
2. Exportez le circuit sous forme de bloc dans votre bibliothèque.
Exercice 3 : Additionneur 4-bits
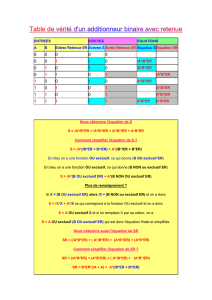
On considère un encodage classique des nombres en binaire. Définissons un additionneur 1-bit avec les
caractéristiques suivantes :



L'opérateur a trois entrées A, B et Re.
L'opérateur a deux sorties S et Rs.
Les deux bits de sorties correspondent au résultat de l'addition des trois bits d'entrée (Rs sera le
bit de poids fort).
1. Réalisez le circuit de l'opérateur.
2. Exportez le circuit ainsi créé et utilisez-le pour réaliser un additionneur opérant sur deux entrées
de 4 bits. Cet additionneur aura toujours une entrée Re et une sortie Rs sur un bit. Pensez à
utiliser le groupement de fils pour les entrées.
3. Exportez votre additionneur 4 bits. Réalisez un additionneur 4-bits avec détection d'overflow : si
le résultat produit un overflow, le résultat renvoyé est la valeur maximale sur 4-bits, sinon la
valeur renvoyée correspond au résultat. Comme pour l'exercice 1, utilisez les switchs et les leds
de la carte pour tester le circuit.
Exercice 4 : Bonus
Considérons maintenant un additionneur 32-bits réalisé en suivant l'approche de l'exercice 3.
1. Quelle est la longueur du chemin critique de l'additionneur ? Généralisez en donnant une
tendance en fonction du nombre de bits de l'additionneur.
On considère maintenant un encodage différent : chaque chiffre est encodé sur deux bits (les chiffres
possibles vont donc de 0 à 3) mais la valeur d'un nombre à deux chiffre se calcul comme en base deux :
'ab' = a*2 +b avec a et b entre 0 et 3.
Par exemple : '00' vaut 0 ; '10' vaut 2 ; '20' vaut 4 ; '30' vaut 6 ; '22' vaut 6.
On note que cet encodage introduit de la redondance.
2. Réalisez le circuit d'un additionneur 1-bit avec cet encodage. Ce circuit ne comportera pas
d'entrée Re mais aura toujours une sortie Rs sur 1 bit.
3. Comment pouvez-vous utiliser cette brique de base pour réaliser un additionneur 4-bits ? Quel
est l'avantage de cet additionneur par rapport à celui de l'exercice 3 ? Pourquoi ce procédé n'est
pas utilisé dans les ordinateurs actuels (intuitivement).