Interféromètre de Fabry

Simulation informatique
d'une figure d'interférences
d'un interféromètre de
Fabry-Perot.
Principe de l'interféromètre.
Schéma de principe d'un
interféromètre de
Fabry-Perot : les rayons
lumineux sont réfléchis à
l'intérieur de la cavité, et en
ressortent partiellement.
Interféromètre de Fabry-Perot
L'
interféromètre de Fabry-Perot
est un
interféromètre
optique constitué de deux
surfaces partiellement réfléchissantes
planes à hauts
coefficients de réflexion
(souvent
supérieurs à 95 %). Il doit son appellation à
Charles Fabry
et
Alfred Perot
.
La lumière entrante effectue de multiples aller-retour à l'intérieur de cette
cavité
, et ressort
partiellement à chaque réflexion. Les différents
rayons lumineux
sortants
interfèrent
entre
eux, donnant lieu à une
figure d'interférences à ondes multiples
constituée d'anneaux
concentriques fins.
Sommaire
1
Description de l'appareil
2
Principe de l'interféromètre pour une onde monochromatique
3
Transmission en fonction de la longueur d'onde
4
Finesse de l'interféromètre
5
Applications
6
Voir aussi
7
Liens externes
8
Bibliographie
9
Référence
Description de l'appareil
L'interféromètre est constitué d'une paire de lames à faces parallèles ou quasiment
parallèles, semi-réfléchissantes. Les faces ont en général un léger angle (une fraction de
degré
), pour éviter des franges d'interférence dues aux faces arrières ; lesdites faces
arrières ont en général un
traitement antireflet
. Le système comporte en sortie une lentille
de focalisation.
Le système est typiquement éclairé par un faisceau collimaté.
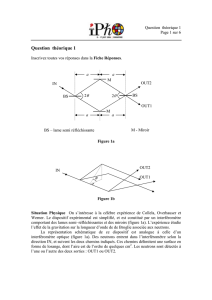
Principe de l'interféromètre pour une onde
monochromatique
Pour simplifier l'étude, on suppose que l'interféromètre est éclairé par une source de
lumière
monochromatique
. On peut représenter, comme sur la figure ci-contre, un rayon en
particulier, et calculer sa contribution à la lumière sortante.
Les rayons lumineux sortant par la deuxième surface aux points
b
et
c
n'ont pas parcouru la
même longueur de trajet (ou
chemin optique
). Ainsi, ils présentent un
déphasage
l'un par
rapport à l'autre, dépendant de l'angle
. Ces deux rayons interfèrent entre eux ainsi
qu'avec tous les autres rayons qui auront été réfléchis plusieurs fois entre les deux surfaces
réfléchissantes. On peut alors montrer que, selon la valeur de
, le rayon est transmis ou
pas.
On s'aperçoit en fait que seules quelques valeurs de
permettent de transmettre la lumière
du rayon incident. Chacune de ces valeurs peut être directement visualisée : elles
correspondent à une série d'anneaux concentriques observés sur la figure d'interférence.
En effet, en plaçant une
lentille convergente
à la sortie de l'interféromètre, tous les rayons
faisant le même angle
par rapport à l'axe central de la lentille formeront un anneau.
Comme expliqué dans l'article
interférence par une couche mince
, le déphasage entre deux
rayons successifs est donnée par :
où n est l'indice de réfraction de la couche, l son épaisseur,
l'angle de réfraction et
où
est la longueur d'onde.
La phase du m-ième rayon est alors :
1
Interféromètre de Fabry-Perot — Wikipédia https://fr.wikipedia.org/wiki/Interféromètre_de_F...
1 sur 3 20/05/2015 18:52

Courbes de la transmittance
de l'interféromètre de
Fabry-Perot en fonction de
la longueur d'onde.
Courbe représentant la
finesse d'un interféromètre
de Fabry-Perot en fonction
du coefficient de réflexion
des miroirs formant la
cavité.
Or le rayon m a subi deux réflexions de plus que le précédent si bien que chaque réflexion atténuant l'intensité lumineuse
d'un facteur
, l'amplitude (qui est proportionnelle à la racine carrée de l'intensité) est atténuée d'un facteur
à
chaque réflexion. En notant
l'amplitude complexe du rayon incident et
l'amplitude complexe du premier rayon qui sort
de la couche mince, on en déduit l'amplitude complexe du m-ième rayon :
Or le premier rayon qui sort de la couche mince a subi deux réfractions par rapport au rayon incident, chaque réfraction
multipliant l'intensité lumineuse par
. L'amplitude est donc multipliée par
à chaque réfraction ; ainsi,
l'amplitude du premier rayon qui sort de la couche mince, étant réfracté deux fois par rapport au rayon incident, s'écrit :
.
Si on place alors une lentille convergente qui fait converger tous ces rayons vers un même point d'un écran placé au plan
focal, l'amplitude de l'onde au niveau de cet écran s'écrit alors comme la somme des contributions de chaque rayon :
En notant
l'intensité lumineuse du rayon incident, l'intensité lumineuse de tous ces rayons qui converge vers un même
point de l'écran est alors :
La transmittance est alors :
Transmission en fonction de la longueur d'onde
La figure d'interférence obtenue présente toujours des anneaux concentriques, mais leur
taille varie en fonction de la distance entre les deux surfaces réfléchissantes, et de la
longueur d'onde
de la lumière utilisée. En effet, lorsqu'on étudie la formule précédente on
s'aperçoit que seules quelques longueurs d'ondes sont transmises : la transmittance en
fonction de
présente des pics séparés de
et d'une largeur
.
La courbe correspondant à la transmittance en fonction de l'angle
dépend de la longueure
d'onde
si bien qu'à chaque longueur d'onde correspond son propre
système d'anneaux
. En
présence de plusieurs longueurs d'ondes, on peut comparer ces différents systèmes
d'anneaux afin de mesurer les longueurs d'ondes. Cet interféromètre est donc utilisé en
spectrométrie
.
Finesse de l'interféromètre
Pour pouvoir mieux séparer les différents anneaux, il est intéressant qu'ils soient les plus
fins possibles. Cela est équivalent à
affiner
les pics de la courbe précédente, c'est-à-dire à
réduire
par rapport à
. Ainsi, un interféromètre de bonne qualité présentera un
beaucoup plus faible que
.
Pour simplifier, on utilise la grandeur suivante, appelée
finesse
:
Et donc, plus la finesse est importante, plus les anneaux sont fins. Afin d'augmenter cette
finesse, il est possible de rendre les surfaces formant la cavité très réfléchissantes. En effet,
on peut montrer, comme l'illustre la courbe ci-contre, que la finesse augmente avec le
coefficient de réflexion
des surfaces.
Ainsi les interféromètre de Fabry-Perot dans le commerce peuvent avoir des finesses valant
quelques dizaines voire quelques centaines. En recherche on peut même aller jusqu'à quelques centaines de milliers.
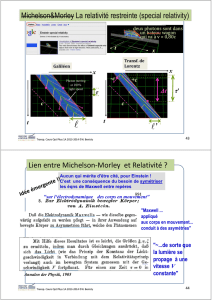
Cette finesse élevée est un atout important de ce type d'interféromètres par rapport à l'
interféromètre de Michelson
, qui a
une finesse de 2.
Interféromètre de Fabry-Perot — Wikipédia https://fr.wikipedia.org/wiki/Interféromètre_de_F...
2 sur 3 20/05/2015 18:52

Un dispositif Fabry-Perot
commercial
La finesse peut-être reliée au temps de vie
des photons dans la cavité et à l'intervalle spectral libre en fréquence ISL :
Ainsi, le nombre d'oscillations N effectuées par la lumière dans la cavité est d'autant plus grand que la finesse est élevée :
Applications
Les utilisations possibles sont :
dans le domaine de la
spectroscopie
(séparation de longueurs d'ondes très voisines)
la réalisation de
filtres interférentiels
très sélectifs (ne laissant passer qu'une plage de
longueurs d'ondes de l'ordre de 10 nm).
la réalisation de
cavités laser
, les miroirs ne sont plus plans mais concaves afin de limiter
au maximum les pertes
le contrôle de la longueur d'onde des signaux pour certaines télécommunications.
Voir aussi
Interférométrie
Interférence
Interféromètre de Michelson
Liens externes
Simulations informatiques:
Simulation complète des principaux dispositifs d'interférométrie. Université Paris XI
(
https://sites.google.com
/site/enseignementphysiqueclassique/optique
)
Bibliographie
G. Hernandez,
Fabry-Perot Interferometers
, Cambridge, Cambridge University Press,
1986
(
ISBN
0-521-32238-3
)
Référence
The Fabry-Perot Interferometer: History, Theory, Practice and Applications
(https:
//books.google.com/books?id=mMLuISueDKYC&pg=PA8
)
sur
Google Livres
1.
Ce document provient de «
http://fr.wikipedia.org
/w/index.php?title=Interféromètre_de_Fabry-Perot&oldid=111367315
».
Dernière modification de cette page le 29 janvier 2015 à 12:12.
Droit d'auteur
: les textes sont disponibles sous
licence Creative
Commons paternité partage à l’identique
; d’autres conditions peuvent
s’appliquer. Voyez les
conditions d’utilisation
pour plus de détails, ainsi
que les
crédits graphiques
. En cas de réutilisation des textes de cette page, voyez
comment citer les auteurs et mentionner
la licence
.
Wikipedia® est une marque déposée de la
Wikimedia Foundation, Inc.
, organisation de bienfaisance régie par le
paragraphe
501(c)(3)
du code fiscal des États-Unis.
Sur les autres projets Wikimedia :
Interféromètre de Fabry-Perot
(https:
//commons.wikimedia.org
/wiki/Category:Fabry-
P%C3%A9rot_interferometer?uselang=fr
)
,
sur
Wikimedia Commons
Interféromètre de Fabry-Perot — Wikipédia https://fr.wikipedia.org/wiki/Interféromètre_de_F...
3 sur 3 20/05/2015 18:52