Chp 7 performances et dependance de l attraction terrestre

Seconde_Thème 3_LE SPORT
chapitre 7_Performances et dépendance de l’attraction terrestre
M.Meyniel 1/4
PERFORMANCES ET DEPENDANCE DE L’ATTRACTION TERRESTRE
Nos performances sportives dépendent du milieu dans lequel on se trouve, sous l’eau comme en
altitude. Elles demeurent toutes liées au fait que nous sommes continuellement attirés par le centre de la Terre : on
coule comme on tombe. Isaac Newton a alors introduit la notion de gravité : ce qui oblige tout corps situé à la surface
de la Terre à se diriger vers son centre. Nos performances dépendant de cette gravité, il convient de l’étudier ici.
Dans un premier temps, nous étudierons cette action mécanique que nous subissons et qui nous attire vers le centre de
la Terre : la gravitation universelle. Puis, dans le but de conclure notre étude sur le Sport, nous nous intéresserons plus
particulièrement à cette action au voisinage de la Terre que l’on nomme alors la pesanteur. Enfin, pour boucler la
boucle sur tout notre travail de l’année, nous étendrons progressivement notre analyse à l’Univers tout entier en
observant ce qui se passe au-delà de notre planète, dans l’Univers.
I. La gravitation universelle.
1. L’interaction gravitationnelle.
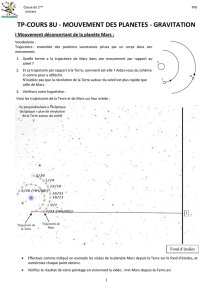
Observations : Si on lance un javelot en aluminium (d’une masse de 500 g) le plus loin possible, il retombe
toujours sur Terre. On en déduit que la Terre attire le javelot ; tout comme elle attire la Lune.
Par ailleurs, la réciproque est vraie : la Lune attire la Terre comme le prouvent le phénomène
de marée ; et il en va de même pour le javelot bien que le phénomène ne puisse s’observer du fait de
la masse de la Terre très grande devant celle du javelot.
Au vu des observations, que peut-on dire de deux corps ayant une masse ?
Comment qualifier l’interaction qui en résulte ?
Rq : * L’attraction n’est pas visible en elle-même, on peut uniquement en voir les conséquences (chute, marée, …).
* Le corps ayant la masse la plus faible présente un mouvement plus visible (car son inertie est plus faible).
2. Loi de l’attraction gravitationnelle (1687). (Isaac Newton, 1642-1727)
Deux corps ponctuels A et B, de masse respectives mA et mB, séparés d’une distance d = AB
exercent l’un sur l’autre des forces d’attraction gravitationnelles  et  qui ont:
- une même direction : celle de la droite (AB)
- des sens opposés : dirigés vers le centre attracteur : vers A pour  et vers B pour 
- une même intensité :
Proposer une représentation graphique illustrant la loi de gravitation universelle
et rappeler l’expression de l’intensité de la force gravitationnelle.
Comment évolue la force si la distance entre les deux corps augmente ? Justifier.
Rq : * Deux corps sont dits ponctuels si leurs dimensions sont petites par rapport à la distance qui les sépare.
FG = FA/B = FB/A = 𝑮𝒎𝑨𝒎𝑩
𝒅
N
kg
m
avec G : constante de gravitation universelle G = 6,67.10-11 N.m².kg-2

Seconde_Thème 3_LE SPORT
chapitre 7_Performances et dépendance de l’attraction terrestre
M.Meyniel 2/4
3. Caractère universelle de la loi gravitationnelle.
* Les électrons et les noyaux d’un atome sont considérés comme ponctuels du fait de leur
taille et de la distance qui les séparent.
* Tous les astres (planètes, étoiles) sont des corps à répartition sphérique de masse c’est-à-
dire que la matière est répartie sous forme de couches concentriques homogènes (comme la Terre qui
présente un noyau au centre, entourée de l’asthénosphère elle-même entourée par la lithosphère). On peut
alors considérer que toute la masse se tient au centre. On les modélise alors par des systèmes ponctuels
notamment au vu des distances qui séparent les astres.
* Les objets au voisinage d’un astre sont de petites dimensions par rapport à la distance qui
les sépare du centre de l’astre. En considérant le centre de gravité de ces objets et le centre de l’astre, on est
de nouveau en présence de systèmes ponctuels.
 Tous les systèmes précédents peuvent être considérés comme ponctuels. La loi de gravitation
universelle s’applique en considérant que toute la masse des corps se concentre en leur centre.
La loi d’attraction gravitationnelle revêt donc un caractère ………………………… .
Rq : * Dans une boule de billard comme un poids d’athlétisme, la matière est répartie uniformément donc il
s’agit d’un corps à répartition sphérique de masse : la loi gravitationnelle s’applique encore et toujours !
* La gravitation universelle assure la cohésion du système solaire et de l’Univers par son caractère attractif.
Exercice d’application : Soit un javelot de masse mJ = 500 g lancé à une hauteur h = 15 m de la
surface terrestre.
La Terre a une masse MT = 5,97.1024 kg et un rayon moyen RT = 6 371 km.
1. Schématiser la situation.
2. a. Exprimer l’intensité FT/J de la force d’attraction gravitationnelle exercée par la Terre
sur le javelot.
b. Calculer la valeur de cette force.
c. Justifier l’utilisation de la loi d’attraction gravitationnelle.
3. Que vaut alors l’intensité de la force d’attraction  exercée par le javelot sur la Terre ?
4. Représenter les forces sur le schéma.

Seconde_Thème 3_LE SPORT
chapitre 7_Performances et dépendance de l’attraction terrestre
M.Meyniel 3/4
II. La pesanteur.
1. Poids et attraction terrestre.
Observations : Au voisinage de la Terre, tout corps ayant une masse est attiré vers le centre de la
Terre du fait de l’attraction gravitationnelle. Cette sensation s’appelle la pesanteur.
Comment appelle-t-on communément cette force responsable de cette attraction terrestre ?
Préciser ses caractéristiques.
Quel type de relation existe-t-il entre le poids P et la masse m d’un corps ? En déduire une
représentation graphique correspondante.
2. L’intensité de pesanteur.
Calculer le poids P d’un javelot en aluminium de masse mJ = 500 g.
Comparer votre résultat à l’intensité FT/J et en tirer une conclusion entre la force d’attraction gravitationnelle
subie par un corps FT/corps et son poids P.
En déduire une expression de l’intensité de pesanteur g et estimer sa valeur à la surface de la Terre.
3. Variation de poids et performances sportives.
Quelle que soit notre position dans l’Univers, nous possédons toujours le même nombre de
cellules, donc de molécules, donc de particules. Il en va de même pour tous les objets de l’Univers.
Quelle grandeur caractéristique d’un corps reste alors constante quelle que soit notre position dans l’Univers ?
Par contre, l’intensité de pesanteur g peut varier puisqu’elle dépend de la distance au centre et
de la masse de l’astre considéré.
En conséquence, selon notre position sur Terre et dans l’Univers, quelle grandeur varie ?
Conséquences :
 Sur Terre : * Plus un corps monte en altitude, plus il s’éloigne du centre de la Terre. Il subit
donc de moins en moins l’attraction terrestre : l’intensité de pesanteur g diminue alors avec
l’altitude (En effet, la distance est au dénominateur !). Mais cela demeure négligeable si l’altitude h
reste très petite devant le rayon de la Terre RT (ce qui est le cas pratique pour nous) : h << RT
* Du fait de la force centrifuge et de l’aplanissement de la Terre aux pôles,
l’intensité de pesanteur augmente avec la latitude. Ainsi : gpôle = 9,83 > géquateur = 9,78 [N.kg-1]
 Sur les autres astres : * La masse et le rayon variant d’un astre à l’autre, l’intensité de pesanteur
varie en conséquence.
Cas de la Lune : gLune = 
 =   = 1,62 N.kg-1
=> 
  ≈ 6
L’intensité de pesanteur est 6 fois plus faible sur la Lune que sur la Terre. Un objet y
possède un poids 6 fois moins intense que sur Terre. Il subit donc une inertie 6 fois plus
faible, expliquant les bonds sur la Lune et les records de lancer, de saut potentiellement
améliorables … !

Seconde_Thème 3_LE SPORT
chapitre 7_Performances et dépendance de l’attraction terrestre
M.Meyniel 4/4
III. Observation de la Terre et de l’Univers.
1. Observer la Terre et son voisinage : les satellites.
 La Lune est le seul satellite naturel de la Terre. Elle réalise le tour de la Terre en 29 jours environ en décrivant un
mouvement circulaire uniforme dans le référentiel géocentrique (rattaché au centre de la Terre).
Rq : * Son mouvement n’étant pas rectiligne uniforme. D’après le principe d’inertie, cela induit qu’elle est soumise à des forces
qui ne se compensent pas. En effet, elle ne subit qu’une seule force : la force d’attraction gravitationnelle qu’exerce la Terre sur
elle, en d’autres termes : le poids de la Lune.
 Depuis 1957, de nombreux satellites artificiels ont aussi été envoyés autour de la Terre par l’Homme :
- des satellites comme Météostat fournissent aux météorologues des données pour étudier
l’atmosphère, faire des prévisions, annoncer des cyclones ou des tempêtes, suivre l’évolution du climat. De
façon à pouvoir délivrer des informations en continu, ces satellites demeurent toujours à la même verticale
d’un même point géographique. Un tel satellite est dit géostationnaire, c’est-à-dire fixe par rapport à
référentiel terrestre (mais il possède un mouvement circulaire uniforme par rapport au référentiel
géocentrique puisqu’il tourne autour du centre de la Terre en même que la Terre elle-même) ;
- le « GPS » (Global Positioning System) utilise de la même façon au moins trois satellites afin de
déterminer une position dans l’espace pour un automobiliste, un marin ou encore un randonneur. Par ailleurs,
ce système permet aussi de rendre compte de la dérive des continents, de travailler à la prévision des séismes
ou des tsunamis pour les géophysiciens, … Les européens ont lancé le programme Galiléo, depuis quelques
années, pour concurrencer le système américain GPS.
2. Observer le reste de l’Univers : les sondes.
 Le Soleil et toutes les planètes du système solaire ont été étudiés grâce aux données fournies par des sondes (et
parfois des robots) :
- la sonde SOHO (Solar and Heliospheric Obervatory) est en orbite autour du Soleil depuis 1995 pour
l’étudier ;
- la sonde Galileo, envoyée en 1989 et arrivée au voisinage de Jupiter fin 1995, a permis l’étude du
système jovien, c’est-à-dire Jupiter et ses satellites, jusqu’en 2003 avant de se désintégrer près du satellite
Europe pour éviter toute pollution par des bactéries terrestres ;
- la sonde Curiosity s’est posé sur le sol de Mars en août 2012 …
 Des sondes spatiales - Rosetta par l’Agence Spatiale Européenne « ESA » ; Deep Impact par la NASA « National Aeronautics
and Space Admnistration » - sont aussi envoyées vers les comètes et leur noyau afin d’apporter des renseignements sur
le passé du système solaire et de l’Univers.
 Depuis 1990, le télescope spatial Hubble est en orbite à 600 km au-dessus de la Terre. Bien que proche de la Terre,
sa position en dehors de l’atmosphère terrestre a permis, en s’affranchissant de la pollution atmosphérique, de
découvrir de nouvelles planètes, étoiles et galaxies ainsi que de fournir des images et données permettant la
modélisation de l’Univers. Les sondes Voyager I et II lancées pour étudier le Système Solaire.
Compétences exigibles
- Calculer la force d’attraction gravitationnelle qui s’exerce entre deux corps à répartition sphérique de masse.
- Savoir que la pesanteur terrestre résulte de l’attraction terrestre.
- Comparer le poids d’un même corps sur la Terre et sur la Lune.
- Analyser des documents scientifiques portant sur l’observation du système solaire.
- Mettre en œuvre une démarche d’expérimentation utilisant des techniques d’enregistrement pour comprendre la
nature des mouvements observés dans le système solaire.