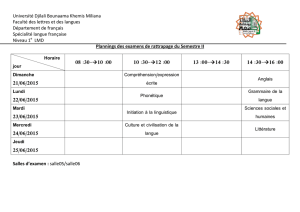
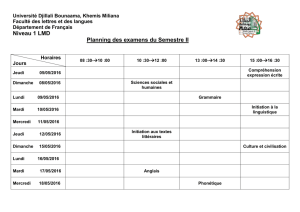
Chapitre 2 : Le formalisme de la physique statistique

Faculté des Sciences et de la Technologie Fonction de la Variable Complexe
Université Djilali Bounaama - KHEMIS MILIANA 2ème année Licence : Physique
1
Chapitre 03 : Fonctions élémentaires
I. Fonction exponentielle complexe :
On rappelle la définition d’une fonction exponentielle complexe :
Déf. I.1 :
La fonction  définie par :
 Est appelée fonction exponentielle complexe.
Pour une fonction exponentielle complexe, les propriétés sont similaires
avec une exponentielle réelle, telle que la différentiabilité partout sur R
de  : 
.
Théorème I.1 :
La fonction exponentielle  est entière et sa dérivée est donnée par :
On vérifie bien que pour  est analytique et
répond aux conditions de Cauchy-Riemann :
En plus du fait que la dérivée de  :
Exemple 1. : Calculer les dérivées des fonctions suivantes :
I.2. Module, argument et conjugué de  :
Si on pose  dans la forme polaire, alors on peut l’écrire :
Par identification, on trouve :
Vérifiant bien que :  ; du moment que dans R : 
Et 
Un résultat important est déduit : .
Le conjugué de  est également obtenu :
Ceci conclut donc que : 
I.3. Propriétés algébriques :
Si  et  sont deux complexes alors on a :
(1) 
(2) 
(3) 
(4) 
I.4. Périodicité de  :
Comme  définie par les deux fonctions cosinus et sinus ; qui sont elles-
mêmes périodiques, on en déduit que la fonction  est également
périodique de période :  

Faculté des Sciences et de la Technologie Fonction de la Variable Complexe
Université Djilali Bounaama - KHEMIS MILIANA 2ème année Licence : Physique
2
« La fonction exponentielle complexe est périodique avec une période
purement imaginaire  :  »
Ceci peut être également vérifié pour :  .
Mais la première région de périodicité  est définie comme
« région fondamentale ».
Figure 1. Région fondamentale de exp(z)
I.5. Transformation sous  :
Comme  on s’intéresse aux cas suivants :
Cas 1 : z est une ligne verticale :  :
Donc sous  
Ceci montre que pour toute région périodique sous  donne lieu à un
ensemble de cercles concentriques de rayon  :
Figure 2. Transformation de segments verticaux sous exp(z)
Cas 2 : z est une ligne horizontale : 
Donc sous  
Figure 3. Z est sous forme de lignes horizontales
Les images  ce sont des segments droits de longueur
 et qui sont portés sur une direction définie par l’argument b.

Faculté des Sciences et de la Technologie Fonction de la Variable Complexe
Université Djilali Bounaama - KHEMIS MILIANA 2ème année Licence : Physique
3
Figure 4. Image sous exp(z) de lignes horizontales
On résume les propriétés des transformations sous  comme suit :
(i)  transforme la région fondamentale 
 en un ensemble 
(ii)  transforme le segment vertical :  en un
cercle 
(iii)  transforme la ligne horizontale  en un
rayon porté sur un angle 
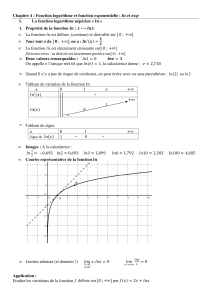
II. Fonction logarithme complexe :
Comme on l’a déjà vu dans la fonction exponentielle complexe, elle
n’est pas une fonction univoque comme c’est le cas pour la fonction
exponentielle réelle. Ceci dit, dans la plan des complexes C et pour un
complexe donné fixe et non nul, l’équation :  a une infinité de
solutions (à cause de la périodicité de l’argument). Ceci peut être mieux
expliqué en supposant :  une solution de l’équation  et
dans ce cas on écrira :  et  et il en découle de
l’identification que :  et  ou d’une manière
équivalente :  et . Cependant, pour un complexe
non nul z on peut montrer que :
A cause de l’infinité des arguments de z, l’équation ci-dessus donne une
fonction multivaluée (à valeurs multiples)  qui est donnée par la
définition suivante :
Déf.II.1.
La fonction multivaluée  définie par :
 Est appelée le Logarithme Complexe de z.
En utilisant la notation exponentielle de , alors on peut réécrire
le logarithme complexe de z dans la forme suivante :
 avec .
Remarque : la notation  est utilisée pour définir le logarithme
népérien (à base de e) de la valeur réelle positive non nulle x.
Exemple 2. Trouver toutes les solutions complexes des équations
suivantes :
II.1. Les identités logarithmiques :
Les identités suivantes sont facilement démontrables par la définition
II.1, qui sont analogues aux identités logarithmiques réelles :

Faculté des Sciences et de la Technologie Fonction de la Variable Complexe
Université Djilali Bounaama - KHEMIS MILIANA 2ème année Licence : Physique
4
Si  et  sont des nombres complexes non nuls et n un entier, alors :
(i) 
(ii) 
(iii) 
II.2. Valeur principale du logarithme complexe :
La fonction complexe  définie par :
Est appelée la valeur principale du logarithme complexe.
Exemple 3. Calculer ;es valeurs principales du logarithme complexe
 pour :
II.3. La fonction  inverse de la fonction  :
Si la fonction exponentielle complexe  est définie sur la région
fondamentale, donc  est une fonction
univoque (un-à-un) et la fonction inverse de  est la valeur principale
du logarithme complexe : .
II.4. Analyticité du logarithme complexe :
Comme la fonction logarithme complexe est une fonction multivaluée
donc elle ne vérifie pas les conditions de continuité et dérivabilité sur
tout le plan complexe, c’est pour ainsi qu’on définit une fonction
logarithmique complexe définie sur le domaine  ou
. On parle dans ce cas d’une fonction logarithme
complexe qui constitue une Branche Principale de . Cette
branche est définie comme :
 avec 
Ce qui exclut tout .
Figure 5. Domaine de définition de 
Ceci nous permet d’obtenir une fonction analytique sur ce domaine :
continue et dérivable qui vérifie le théorème suivant :
Théorème.II.1. Analyticité de la branche principale de lnz
La branche principale  du logarithme complexe définie par :
 avec 
Est une fonction analytique et sa dérivée est donnée par :

Faculté des Sciences et de la Technologie Fonction de la Variable Complexe
Université Djilali Bounaama - KHEMIS MILIANA 2ème année Licence : Physique
5
Exemple 4. Trouver les dérivées des fonctions suivantes dans le
domaine approprié :
II.5. Transformations sous  :
Comme la fonction  constitue une fonction inverse de l’exponentielle
complexe  on peut déduire les propriétés de transformation suivantes
sous une fonction logarithmique complexe :
(i)  transforme l’ensemble  en une région
(ii)  transforme un cercle définie par  en une un
segment de ligne verticale 
(iii)  transforme un rayon  en une ligne
horizontale 
III. Puissance complexe :
On sait déjà comment manipuler une puissance entière d’un nombre
complexe du type , par contre lorsqu’il s’agit d’un exposant
complexe, il n’est pas évident de calculer ou de résoudre une
expression comme : , pour cela on fait appelle au deux fonctions
exponentielle complexe et logarithme complexe :
Def. III.1. :
Si  est un nombre complexe et , alors la puissance complexe 
est définie comme : 
Il est possible de vérifier que pour un exposant n entier, la fonction
puissance  est une fonction univoque, par contre lorsqu’il s’agit d’un
exposant complexe comme c’est le cas pour  on parle ici d’une
fonction puissance complexe multivaluée.
Exemple 5. Trouver les valeurs des puissances complexes suivantes :
Les puissances complexes définies plus haut, vérifient les propriétés
suivantes qui sont analogues dans le cas des puissances réelles :
(i) 
(ii) 
(iii) 
III.1. Valeur principale d’une puissance complexe :
On rappelle que dans la définition III.1 la puissance complexe est une
multivaluée définie avec le  qui est déjà une multivaluée. On peut
définir une valeur principale d’une puissance complexe en utilisant la
valeur principale du logarithme complexe :
Déf. III.2 :
Si  est un nombre complexe et , alors la fonction définie par :
 est appelée La valeur principale de la puissance
complexe 
Exemple 6. Trouver les valeurs principales des puissances complexes
suivantes :