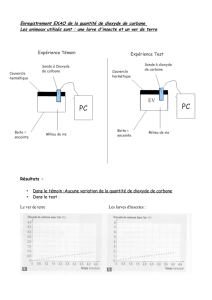
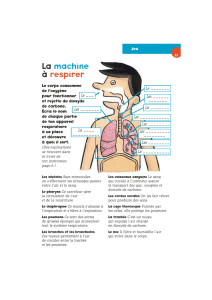
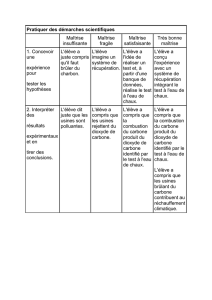
DS N°4 BB_4-02-15

-1-
TERMINALES S1, S2, S3, S4 Mercredi 4 Février 2015
DEVOIR SURVEILLÉ
SCIENCES PHYSIQUES
Durée : 3 heures 30
Toutes les réponses doivent être correctement rédigées et justifiées.
Vous traiterez chaque exercice sur une copie indépendante.
Ce sujet comporte 13 pages dont 4 d’annexes.
Le barème donné est à titre indicatif et pourra être très légèrement modifié.
CALCULATRICE INTERDITE
NE RENDEZ PAS LE SUJET, CONSERVEZ-LE
EXERCICE I : UN PEU DE BALISTIQUE (8,75 pts)
EXERCICE II : MOUVEMENT D’UN ASTÉROÏDE (6,25 pts)
EXERCICE III : LE DIOXYDE DE CARBONE : LE RÉDUIRE DANS L’ATMOSPHÈRE ET LE
VALORISER (à ne pas traiter par les élèves ayant choisi la spécialité « physique ») (5 pts)
EXERCICE IV : IONS CHLORURE DANS L’EAU DE MER (Exercice « spécialité ») (5pts)

-2-
I) UN PEU DE BALISTIQUE (8,75 pts)
Lors de fouilles préventives sur un chantier de travaux
publics, on a retrouvé ce qui ressemble à une arme à feu. Il
s’agit d’un ancien pistolet lance-fusées en bronze datant
probablement de la première Guerre Mondiale. Il est dans
un état de conservation assez remarquable.
Ce type de pistolet était très utilisé lors de cette guerre car,
en plus de lancer des fusées éclairantes, il pouvait servir de
moyen de communication. En effet, à l’époque très peu de
moyens étaient mis à disposition des troupes : les ondes
hertziennes étaient très peu utilisées et c’étaient des
kilomètres de câbles téléphoniques qui devaient être
déroulés pour permettre la transmission de messages
divers et variés.
Ainsi les pistolets signaleurs se sont avérés très utiles.
Pistolet lance-fusées
(d’après www.histoire-collection.com)
1. Durée de visibilité de la fusée
Sur la notice des fusées éclairantes que l’on peut utiliser dans ce type de pistolet, on trouve les
informations suivantes :
- Cartouche qui lance une fusée éclairante s’allumant 1,0 seconde après son départ du
pistolet et éclaire d’une façon intense pendant 6,0 secondes environ.
- Masse de la fusée éclairante : m
f
= 60 g.
On se place dans le référentiel terrestre supposé galiléen.
Le champ de pesanteur terrestre est considéré uniforme, de valeur g = 10 m.s
–2
.
On négligera toutes les actions dues à l’air ainsi que la perte de masse de la fusée pendant qu’elle
brille et on considèrera cette dernière comme un objet ponctuel.
On définit un repère (O,
i
uur
,
j
uur
) avec O au niveau du sol et tel que la
position initiale de la fusée éclairante à la sortie du pistolet soit à une
hauteur h = 1,8 m.
Le vecteur vitesse initiale
0
v
uur
est dans le plan (O, x, y) ; Ox est horizontal et
Oy est vertical et orienté vers le haut.
À l’instant t = 0 s, le vecteur vitesse de la fusée éclairante fait un angle α
égal à 60 ° avec l’axe Ox et sa valeur est v
0
= 50 m.s
–1
. On pourra se référer
au schéma ci-contre.
Aides au calcul :
50
×
sin60 = 43,3 (50
×
sin60)
2
= 1875 4,3
×
4,3 = 18,5
cos60 = 0,50 (50 × cos60)
2
= 625 4,33 × 4,3 = 186
Les équations du second degré suivantes admettent deux solutions :
- 5x
2
+ 43,3x + 1,8 = 0 x
1
= 8,7 et x
2
= - 4,1.10
-2
- 5x
2
+ 25x + 1,8 = 0 x
1
= 5,1 et x
2
= 7,1.10
-2
1.1. Représenter le vecteur champ de pesanteur  sur le schéma donné en figure 1 de l’ANNEXE
À RENDRE AVEC LA COPIE et tracer qualitativement l’allure de la trajectoire suivie par la fusée
éclairante dans ce champ de pesanteur.

-3-
1.2. En utilisant une loi de Newton que l’on énoncera, déterminer les coordonnées du vecteur
accélération de la fusée éclairante : a
x
(t) suivant x et a
y
(t) suivant y, en structurant votre démarche.
1.3. En déduire les expressions des coordonnées v
x
(t) et v
y
(t) du vecteur vitesse de la fusée
éclairante et montrer que les équations horaires du mouvement de la fusée s’écrivent :
x(t) = v
0
.cos(α).t et
y(t) =
20
.sin( ).
2
α
− + +
g
t v t h
avec t en seconde, v
0
en mètre par seconde et x(t), y(t) et h en mètre.
1.4. Etablir l’équation de la trajectoire.
1.5. Déterminer la valeur de la durée du vol de la fusée éclairante.
1.6. Déterminer à partir des graphes de la figure 2 de l’ANNEXE À RENDRE AVEC LA COPIE,
l’altitude à partir de laquelle la fusée commence à éclairer puis l’altitude à laquelle elle s’arrête. Ces
valeurs paraissent-elles adaptées au but recherché ?
1.7. Sans souci d’échelle, représenter sur la figure 1 de l’ANNEXE À RENDRE AVEC LA COPIE
le vecteur vitesse au point S, point le plus haut de la trajectoire de la fusée.
1.8. Montrer que le temps nécessaire à la fusée pour aller de sa position initiale au point S est
t
S
=
×  
et calculer sa valeur.
1.9. En déduire par le calcul l’altitude y
S
en S.
2. Tir vertical
2.1. On fait un essai de tir vertical ascendant (α = 90°) dans le plan (O, x, y) décrit précédemment.
Quelles sont les coordonnées du point S, point le plus haut de la trajectoire de la fusée ?
2.2. Définir le mouvement de la fusée :
2.2.1. avant S.
2.2.2. après S.
3. Etude de l’éjection de la fusée
Par souci de simplification, on ne considère que le système {fusée – pistolet} et on s’intéresse à sa
quantité de mouvement. La masse du pistolet à vide est m
p
= 1,0 kg.
3.1. Exprimer la quantité de mouvement totale
p
0
uur
du système {fusée - pistolet} avant que la fusée
ne quitte le pistolet puis montrer que celle-ci est équivalente au vecteur nul.
3.2. Éjection de la fusée
3.2.1. Que peut-on dire de la quantité de mouvement totale du système {fusée-pistolet} si
l’on considère ce système comme un système isolé au cours de l’éjection de la fusée du pistolet ?
3.2.2. En déduire dans ce cas l’expression vectorielle de la vitesse
p
v
uur
de recul du pistolet
juste après l’éjection de la fusée en fonction de la masse du pistolet m
p
, de la masse de la fusée m
f
et du vecteur vitesse initiale de la fusée
v
0
uur
. Calculer v
p
.
3.2.3. La valeur réelle de la vitesse est différente de la valeur que l’on obtient à la question
précédente. Donner deux justifications expliquant pourquoi on observe une telle différence.

-4-
II) MOUVEMENT D’UN ASTÉROÏDE (6,25 pts)
Les positions de l’astéroïde Eva sont représentées tous les 54 jours à la figure 1 de l’ANNEXE
DE L’EXERCICE II.
L’échelle est indiquée sur la figure. Eva et le Soleil sont représentés par des points.
Donnée :
Constante universelle de gravitation : G = 6,67.10
-11
SI
1. Dans quel référentiel le mouvement de l’astéroïde Eva est-il étudié ?
2. Quel est le mouvement de l’astéroïde Eva dans ce référentiel ? Justifier :
2.1. D’après la chronophotographie de la figure 1.
2.2. En énonçant les lois de Kepler utiles (on pourra compléter la figure 1 de l’ANNEXE).
3. Montrer que les valeurs des vitesses d’Eva en E
1
et E
-1
sont voisines :
v
E1
≈ v
E-1
≈ 2,7.10
4
m.s
-1
.
4. Représenter sur la figure 1 de l’ANNEXE À RENDRE AVEC LA COPIE les vecteurs vitesse
en E
1
et E
-1
en précisant l’échelle utilisée.
5. Définir le vecteur accélération . En déduire la direction et le sens du vecteur accélération
d’Eva en E
0
. Représenter sur la figure 1 de l’ANNEXE à l’échelle 1 cm pour 0,5.10
-3
m.s
-2
en prenant a
0
= 2,0.10
-3
m.s
-2
.
6. Donner l’expression vectorielle de la force d’attraction gravitationnelle 
/
exercée par le
Soleil sur l’astéroïde Eva en E
0
en fonction d’un des vecteurs unitaires du repère de Frenet.
Comparer et 
/
en direction et en sens. Enoncer la loi de Newton ainsi illustrée.
7. A partir de la 3
ème
loi de Kepler, détailler toutes les étapes nécessaires (sans réaliser les
applications numériques) à la détermination de la masse du Soleil M
s
.
Aides au calcul :
33 / 20 = 1,65 1,5
×
1,65 = 2,48
108
×
24
×
3600 = 9,33.10
6
248 / 933 = 2,66.10
-1

-5-
III) LE DIOXYDE DE CARBONE : LE RÉDUIRE DANS L’ATMOSPHÈRE ET LE VALORISER
(à ne pas traiter par les élèves ayant choisi la spécialité « physique ») (5 pts)
1. Traitement des eaux usées alcalines par le dioxyde de carbone.
Document 1
Pour pouvoir déverser des eaux usées dans les canalisations ou dans les eaux du domaine
public, il faut que celles-ci aient un pH généralement compris entre 6,5 et 8,5.
Les eaux usées alcalines (basiques) peuvent être « neutralisées ›› avec des acides minéraux ;
cependant, le procédé technique est complexe et l'utilisation de ces acides n'est pas sans
problème : corrosion, salinisation (chlorures, sulfates, phosphates, nitrates), risque de
surdosage.
La « neutralisation ›› au dioxyde de carbone s'impose dans la plupart des cas comme la
solution la plus efficace. Les domaines industriels concernés sont multiples: blanchisseries,
industries du papier et de la cellulose, industries textiles, laiteries...
D'après http://www.carbagas.ch et http://www.Iinde-gas
Données :
- Couples acide/base :
H
2
O, CO
2 (aq)
/ HCO
3− (aq)
: pK
A1
= 6,4 (à 25 °C)
HCO
3− (aq)
/ CO
32− (aq)
: pK
A2
= 10,3 (à 25 °C)
H
3
O
+
/ H
2
O
H
2
O / HO
− (aq)
- pK
e
= 14,0 (à 25 °C)
Un groupe d'élèves a comparé la « neutralisation ›› des eaux alcalines par un acide minéral et
par le dioxyde de carbone à l'aide d'un logiciel de simulation.
Dans cette simulation, les eaux usées alcalines sont modélisées par une solution aqueuse
d'hydroxyde de sodium (Na
+ (aq)
+ HO
− (aq)
) notée S, de concentration molaire apportée
c = 1,0.10
−3
mol.L
−1
.
Le document 2 en ANNEXE DE L’EXERCICE III montre l’évolution du pH de la solution S
lorsqu'on ajoute une solution acide. Les solutions acides utilisées sont d'une part, une solution
d'acide chlorhydrique (H
3
O
+ (aq)
+ Cl
− (aq)
), d'autre part une solution aqueuse de dioxyde de
carbone (H
2
O,CO
2 (aq
), de mêmes concentrations molaires apportées c
A
= 1,0.10
−3
mol.L
−1
.
1.1. Écrire l'équation de la réaction qui se produit lors de l’ajout de l’acide chlorhydrique dans la
solution S.
1.2. Dans le cas de la neutralisation par le dioxyde de carbone, quelle est l'espèce carbonatée
qui prédomine (parmi CO
32−
, HCO
3−
et CO
2
) à l'équivalence du titrage ? (on pourra faire
apparaître tout tracé utile sur le document 2 de l’ANNEXE DE L’EXERCICE III). Justifier.
1.3. En déduire l'équation de la réaction lors de l’ajout de la solution de dioxyde de carbone
dans la solution S.
1.4. Comparer les points d’équivalence et interpréter le résultat grâce au document 1.
1.5. Soit V
E
le volume à l'équivalence. Pour les deux neutralisations, évaluer graphiquement les
variations du pH autour de V
E
± 2 gouttes. On supposera que deux gouttes correspondent à un
volume de 0,1 mL.
En déduire la neutralisation la plus adaptée au traitement des eaux usées.