Ondes électromagnétiques dans le vide

Ondes électromagnétiques dans le vide
Physique PC Physique des ondes
Introduction
•Prévues par la théorie de Maxwell dés 1864
•Découvertes par Hertz en 1886
•Problème du support des ces ondes. Expériences de Michelson-Morley
•Domaine des ondes électromagnétiques. Longueur d’onde λ: 1015 m au km ou encore, pour la
période Tet la fréquence f, 10−23 s ( 1023Hz)à 10−5s (105Hz). Le domaine important des ondes
lumineuses, λest compris entre 400 nm et 750 nm, soit 1,2.10−15 s à 2,5.10−15 soit 8,3.1014 Hz à
4,0.1014 Hz.
I. Propagation du champ électromagnétique
I.1 Compréhension intuitive du phénomène
I.2 Équations de propagation du champ électromagnétique →
E,
→
B
Il faut prendre le rotationnel de l’équation → rot
→
E=−∂
→
B
∂t .
On obtient →
∆
→
E−1
c2
∂2→
E
∂t2= 0. De même →
∆
→
B−1
c2
∂2→
B
∂t2= 0 Avec µ0.ε0.c2= 1.
I.3 Le problème du référentiel : de Maxwell à Einstein.
Dans quel référentiel sont exprimées les équations de Maxwell ?
II. Une solution particulière des équations de propagation : le mo-
dèle de l’onde électromagnétique plane progressive dans le vide
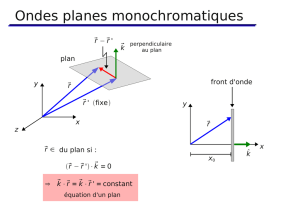
II.1 Définition de l’onde plane et équation d’onde
Une onde est dite plane quand le champ →
E,
→
Bne dépend que d’une variable de l’espace : utel que
u=→
r.→
eu=xα +yβ +zγ. → euest le vecteur unitaire donnant la direction de propagation.
Souvent use réduit à l’une des coordonnées du système cartésien (x, y ou z), dans ce cas l’onde est
plane si le champ →
E,
→
Bne dépend que (x, y ou z).
Dans le cas d’une propagation dans la direction des x, n’importe quelle composante du champ n’est
fonction que de x, t.
Le plan formé par x=cte est un plan d’onde.
L’équation d’onde s’écrit quelque soit la composante du champ ∂2
∂x2−1 c2
∂2
∂t2= 0

Physique des ondes Ondes électromagnétiques dans le vide
II.2 Solution générale de l’équation d’onde
En introduisant p=t+x
cet q=t−x con trouve, comme pour toute équation d’onde de D’Alembert,
s(x, t) = f1(t−x
c) + f2(t+x c)
II.3 Onde plane progressive
Par définition, une O.P.P. de direction de propagation → exest une solution particulière de l’équation
d’onde correspondant à une structure particulière du champ électromagnétique dont les 6 coordonnées
sont de la forme : s(x, t) = f(t−x/c). La grandeur propagée n’est pas déformée (l’amplitude du champ)
et se propage à la vitesse c
II.4 Transversalité du champ électromagnétique →
E,
→
B
La composante du champ suivant → exest nul. Le champ est transversal, c.a.d. appartient à un plan ⊥
à la direction de propagation.
II.5 Relation entre →
Eet →
Bpour une onde plane progressive
→
ex∧
→
E
c=
→
B
→
ex,→
Eet →
Bforment un trièdre direct.
II.6 Énergie associé à une onde électromagnétique plane progressive
Rappel : Théorème de Poynting dans le vide. Dans le vide et en absences de charges, une variation
d’énergie électromagnétique se traduit par un rayonnement d’énergie qui est le flux du vecteur de Poynting.
II.6.1 Densité d’énergie et vecteur de Poynting
eem =ε0E2,→
R=c.eem.→
ex
II.7 Vitesse de propagation de l’énergie d’une onde électromagnétique plane
progressive
Finalement, on a ve=h−→
Ri
heemi=c−→
ex
II.8 Rayonnement : Intensité énergétique de l’O.P.P
L’intensité énergétique I=I(M)d’un rayonnement au point Mest la valeur moyenne de la puissance
rayonnée que reçoit par unité de surface un détecteur plan dirigé perpendiculairement à la direction de
propagation du rayonnement.
I=δPray
dS =D
→
R
E
Exemples : Soleil, Laser Mégajoule
II.9 Onde électromagnétique plane progressive et réalité physique
Source de dimension finie : onde sphérique, localement plane. Les idées concernant la réalité de l’O.P.P.
sont à connaître.
J.-F. Reix page 2 / 8 PC

Physique des ondes Ondes électromagnétiques dans le vide
III. Ondes planes progressives monochromatiques (sinusoïdales,
harmoniques) : O.P.P.M., composante abstraite d’un signal
électromagnétique
L’ensemble de cette étude est à connaître ainsi que le cadre dans lequel elle a pu être faite.
III.1 Etude du spectre électromagnétique
III.1.1 La lumière : partie visible du spectre
III.1.2 Le reste du spectre électromagnétique
III.1.3 Distribution en fréquence de l’énergie d’un signal électromagnétique
I=
∞
Z
0
Iω(ω).dω où Iω(ω)la fonction de distribution en pulsation de ce signal.
Conclusion : Un signal aussi fin soit-il n’est pas rigoureusement monochromatique. Son énergie s’étale
toujours sur une largeur ∆ω.
Caractère abstrait d’une composante monochromatique. L’onde monochromatique n’est pas une réalité
physique mais une composante abstraite faisant office d’outil analytique et à partir de laquelle un signal
réel peut être décrit par superposition.
III.2 Ondes planes progressives monochromatiques
III.2.1 Définition
Une onde plane progressive est dite monochromatique si la fonction f1(t−u/c)est une fonction sinusoï-
dale. Pour une composante des 6 composantes du champ s=smcos (ωt −kx +ϕ0)avec sml’amplitude,
ω: pulsation, ϕ0est la phase à l’origine du temps et de l’espace.
III.2.2 Vecteur d’onde et module du vecteur d’onde
k≡2π
λ: module du vecteur d’onde et →
k=k. →
ex=2π
λ.→
ex, le vecteur d’onde : il indique la direction
de propagation.
s(x, t) = smcos ωt −
→
k.→
r+ϕ0
III.2.3 Double périodicité de l’O.P.P.M.
•La période temporelle T= 2π/ω
•La période spatiale λ= 2π/k
III.2.4 Notation complexe
On associe une fonction complexe notée s=smexp iωt −
→
k.→
r+ϕ0=smexp iωt −
→
k.→
ravec
sm=smexp (i.ϕ0)
III.3 Equations de Maxwell en notation complexe
div→
B= 0 ⇔ −i.
→
k.
→
B= 0
div→
E= 0 ⇔ −i.
→
k.
→
E= 0
→
rot
→
E=−∂
→
B
∂t ⇔
→
k∧
→
E=ω
→
B
→
rot
→
B=1
c2
∂
→
E
∂t ⇔
→
k∧
→
B=−ω
c2
→
E
J.-F. Reix page 3 / 8 PC

Physique des ondes Ondes électromagnétiques dans le vide
→
∆
→
E−1
v2
∂2→
E
∂t2= 0 ⇔−k2+ω2 c2→
E= 0
A retenir : ∂
∂t • → i.ω.•;∂2 ∂t2• → −ω.•;→
grad • → −i.
→
k.•; div • → −i.
→
k.•;→
rot • → −i.
→
k∧• ;
∆• → −k2.•
Comme on vient d’injecter la solution dans l’équation d’onde, on retrouve la relation de dispersion :
k=ω
c, où cest la célérité de la lumière dans le vide.
Ne pas oublier de repasser en notation réelle.
Important : Les calculs liés aux grandeurs énergétiques peuvent être réalisés de deux façons :
1 - En repassant aux notations réelles avant les calculs de termes quadratiques (énergie, vecteur de
poyntingĚ) ;
2 - En utilisant une méthode décrite dans un document, à partir des grandeurs complexes.
III.4 L’O.P.P.M. en tant que composante abstraite d’un signal réel
Lien entre la largeur fréquentielle et la durée du signal :
∆t.∆ν= 1
III.5 États de polarisation des ondes électromagnétiques planes progressives
monochromatiques (O.P.P.M.) dans le vide
Introduction
L’onde électromagnétique transversale est dite polarisée si l’extrémité du vecteur →
Edécrit au cours du
temps une courbe fermée déterminée La direction de polarisation en un point de l’onde est donnée par la
direction du champ électrique. On définit le plan de polarisation comme le plan contenant →
Eet →
k
III.5.1 Les différents états de polarisation de l’O.P.P.M.
a) Polarisation elliptique
C’est la polarisation la plus générale
b) Polarisation rectiligne
c) Polarisation circulaire
Remarque : →
Bse déduit de →
Epar la relation de structure d’une O.P.P.M.
III.5.2 Comment polariser des ondes électromagnétiques ?
a) Lumière naturelle
b) Polaroïds ; Loi de Malus
c) Applications : Lames à retard
Généralités Une lame à retard possède deux directions perpendiculaires entre-elles ici Oz et Oy et
parallèles au plan de la lame telle que :
– si une onde incidente polarisée rectilignement suivant yentre dans la lame elle se propagera à la
vitesse vy=c/ny
– si une onde incidente polarisée rectilignement suivant zentre dans la lame elle se propagera à la
vitesse vz=c/nz.
J.-F. Reix page 4 / 8 PC

Physique des ondes Ondes électromagnétiques dans le vide
Onde incidente :
→
Ei(x= 0, t) = 
0
EOy cos (ωt)
EOz cos (ωt −ϕ)
Onde dans la lame entre 0< x < e. La vitesse de l’onde n’est pas la même dans les deux direction de
polarisation :
→
Ei(x, t) = 
0
EOy cos (ωt −nyk0x)
EOz cos (ωt −nzk0x−ϕ)
Onde transmise en sortie de lame, en x > e :
→
Et(x, t) = 
0
EOy cos (ωt −nyk0e−k0(x−e))
EOz cos (ωt −nzk0e−k0(x−e)−ϕ)
En changeant l’origine de la phase, tel que ωt −nzk0e−k0(x−e) = ωt′, puis, pour la notation t′=t,
on obtient,
→
Et(x, t) = 
0
EOy cos (ωt)
EOz cos (ωt −(ϕ−φ))
avec φ=k0(ny−nz) = ω.e
c(ny−nz)soit φ=2πδ λavec δ=e(ny−nz)
Lame demi-onde λ
2
L’opération résultant est une opération de symétrie. Par rapport à un axe de la lame.
Lame quart-d’onde λ
4On considérera une onde rectiligne puis circulaire.
III.6 Le rayonnement dipolaire, propagation libre, justification du modèle
d’onde plane
Comme il est indiqué dans le programme officiel " On énoncera sans démonstration la formule donnant
le champ électromagnétique rayonné à grande distance ".
III.6.1 Le modèle du dipôle oscillant
a) Description
b) Les approximations
•Approximation dipolaire : r≫z0
•Vitesse de déplacement non relativiste : z0≪λ
•Zone de rayonnement : r≫λ
Soit : r≫λ≫z0
c) La réalité et le modèle
III.6.2 les expressions de
→
Eet
→
B
→
E(r, t) = sin θ
4πε0
••
p(t−r/c)
rc2
→
eθ
→
B(r, t) = µ0sin θ
4π
••
p(t−r/c)
rc
→
eϕ
en posant t′=t−r/c et en choisissant →
p(t) = p0cos ωt →
ezon obtient :
J.-F. Reix page 5 / 8 PC