Chapitre 6. Les ondes électromagnétiques 1/3

Chapitre 6. Les ondes électromagnétiques
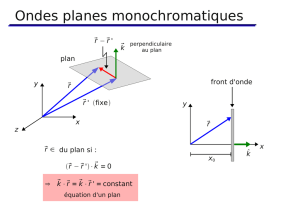
Une$onde$électromagnétique$comporte$à$la$fois$un$champ$électrique$et$un$champ$magnétique$
oscillant$à$la$même$fréquence.$Ces$deux$champs,$perpendiculaires$l’un$par$rapport$à$l’autre$se$
propagent$dans$un$milieu$selon$une$direction$orthogonale$(>igure$ci-dessous).$
Les$ondes$électromagnétiques$sont$des$ondes$transversales$(TEM)$:$les$champs$
⃗
E
et$
⃗
B
sont$perpendiculaires$à$la$direction$de$propagation
Le$rapport$entre$les$deux$grandeurs$E$et$B$est$égal$à$la$célérité$de$la$lumière$dans$le$vide$:
c=E
B
où$:$E$–$l'intensité$du$champ$électrique$(V.m-1),$B-$l'intensité$du$champ$magnétique$($T$-$Tesla)
Les$ondes$électromagnétiques$ont$toutes$la$même$célérité$(ou$vitesse)$de$propagation$dans$le$
vide$:
c=3⋅10
8
m×s
−1
La$célérité$dans$d'autres$milieux$est$toujours$inférieure$à$la$célérité$dans$le$vide.
Imposée$par$la$source,$la$fréquence$f$d'une$onde$électromagnétique$est$indépendante$du$
milieu$de$propagation.$Elle$correspond$au$nombre$d'oscillations$par$seconde$des$champs$
électrique$(
⃗
E
)$et$magnétique$(
⃗
B
).
Période$temporelle$T
T=1
f
où$:$T-$la$période$(en$s),$f-$la$fréquence$(en$Hz)
La$longueur$d'onde$(période$spatiale)
La$longueur$d'onde$λ$correspond$à$la$distance$entre$deux$maxima$d'intensité$du$champ$électrique$et$
1/3

magnétique.$La$période$temporelle$(T)$et$la$longueur$d'onde$(λ$)$dépendent$du$milieu$de$propagation.
c=λ
T=λ⋅f
Le$spectre$électromagnétique$représente$l'ensemble$des$ondes$électromagnétiques.$Seule$une$
in>ime$partie$des$ondes$électromagnétiques,$appelée$lumière$visible,$peut$être$détectée$par$
notre$œil$.$
La$polarisation$d'une$onde$électromagnétique$correspond$à$l'orientation$du$vecteur$champ$
électrique$
⃗
E
lorsqu'un$observateur$regarde$une$onde$se$propageant$vers$son$œil.$
➔La$polarisation$est$linéaire$lorsque$le$champ$électrique$oscille$dans$un$plan$:
➔La$polarisation$est$circulaire$lorsque$le$vecteur$champ$électrique$tourne$autour$
de$la$direction$de$propagation,$sa$norme$restant$constante.$
➔Souvent,$la$norme$du$champ$électrique$varie$périodiquement$en$temps.$On$
parle$en$ce$cas$de$polarisation$elliptique.$
2/3

Le$champ$électrique$d'une$onde$émise$par$une$source$de$puissance$P0$diminue$avec$la$distance
de$la$source$d$selon$la$relation$:
E=
√
αP0
d
où$:$E-intensité$ef>icace$(en$V.m-1),$α-constante$qui$dépend$de$l'antenne,$P0-$puissance$de$la$source$(en
W),$d$–$éloignement$de$la$source$($en$m)
3/3