Jeux entre deux adversaires

Jeux entre deux adversaires
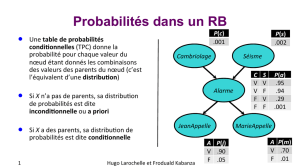
● !"#$%&'$%(")')*$%+%,-.%/$0%,12%
! ,-.%'$3%4'%5*'#1'*%6%(")'*%72"3*'%(")')*8%
! ,12%'$3%$"2%-&/'*$-1*'%
● 92%/-%123'*5*:3'*%4'%*:$)43-3%&;)2'%%
5-*<'%="##'%4-%!"#$%"&'()*+!,'*-+
%./)01-*#-+2'+3)'-'%+425+
! 5')3%/"1*%='>'%*:="#5'2$'%="##'%4'%
*:$)43-3%&;)2%5-*1%
! ,-.%$")?-13'%#-.1#1$'*%$-%*:="#5'2$'%
! ,12%$")?-13'%#121#1$'*%4-%*:="#5'2$'%&'%,-.%
7,12%/-%*'='/"1*%4;"55"$:%&'%='>'%*:="#5'2$'8%
425%
4"*%
@)A"%B-*"=?'44'%'3%C*"&)-4&%D-E-2F-%G%

Arbre de recherche
● H"##'%5")*%4'$%5*"E4I#'$%J)'%KL%5')3%*:$")&*'M%"2%="##'2='%5-*%&:3'*#12'*%4-%
$3*)=3)*'%&'%2"3*'%'$5-='%&'%*'=?'*=?'%
%
● N2%5*"E4I#'%&'%(')%5')3%O3*'%/)%="##'%)2%5*"E4I#'%&'%*'=?'*=?'%&-2$%)2%-*E*'%+%
! N2%*6'!+7.$2$8+"*"(29+:+="2PA)*-<"2%121<-4'%&)%(')+
! N2'%;)*/()*+!-+$%2*#"()*%+%%
» *'3")*2-23%)2%-*#-0&9-+!-+12"%-#+72/()*<+*6'!+#'//-##-'%8+
– -=<"2%5"$$1E4'+74:A-4'8%
– 2Q)&%7:3-38%*:$)43-23%&'%4;'.:=)<"2%&'%='>'%-=<"2+
! N2%$-#$+!-+$-%0"*2"#)*%
» 12&1J)'%$1%4'%(')%'$3%3'*#12:%
! N2'%;)*/()*+!,'(9"$.%5")*%4'$%:3-3$%P2-).%%
7=;'$3%4-%*:="#5'2$'%*'R)'%5-*%4'%(")')*%,-.8%
@)A"%B-*"=?'44'%'3%C*"&)-4&%D-E-2F-%S%

Arbre de recherche tic-tac-toe
@)A"%B-*"=?'44'%T%
:3-3%121<-4%
U"2=<"2%&'%3*-2$1<"2%
U"2=<"2%&;)<413:%

Algorithme minimax
● =!.-+%6%=?-J)'%3")*M%"2%$)55"$'%J)'%4;-=<"2%4-%54)$%5*"P3-E4'%5")*%4'%(")')*%
,-.%")%4'%(")')*%,12%'$3%5*1$'M%=0V6V&0%4-%54)$%A*-2&'%>29-'%+0"*"025+
%
● H'$%:J)-<"2$%&"22'23%)2%1%)?%200-+%./'%#";%5")*%=-4=)4'*%4'$%/-4')*$%5")*%
3")$%4'$%2Q)&$%&-2$%4;-*E*'%&'%*'=?'*=?'%
@)A"%B-*"=?'44'%'3%C*"&)-4&%D-E-2F-%W%
% % %%%%%%%%%%%%%%%%%%%%%%%%%%%%%utilité7n8 % %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%X1%n%'$3%)2%2Q)&%3'*#12-4%
valeurVminimax7n8%Y%%%%%%%%#-.%n’#$)=='$$')*%&'%n#%valeurVminimax7n’8%%%%%%%X1%n%'$3%)2%2Q)&%,-.%%
% % %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%#12%n’#$)=='$$')*%&'%n%%valeur-minimax7n’8%%%%%%%X1%n%'$3%)2%2Q)&%,12%
%

Algorithme minimax
@9?)%"$A0-%minimax7noeudIni*al8%
1. #*'3")*2'%4;-=<"2%=?"1$1'%5-*%3")*,-.7noeudIni*al8#
@)A"%B-*"=?'44'%'3%C*"&)-4&%D-E-2F-%Z%
@9?)%"$A0-%tour-max7n8%
G0 $1%n#="**'$5"2&%6%)2'%P2%&'%5-*<'M%-4"*$%*'3")*2'*%utilité7n8#
2. #u%Y#V[M%a%Y%/"1&%
T0 5")*#=?-J)'#5-1*'#7a’,n’8#&"22:'%5-*%transition7n8%
W0 %$1%4;)<413:%&'%tour-min7n’8%\%u%-4"*$%-]'=3'*%a%Y%a’M%u%Y%)<413:%&'%tourVmin7n’8%
5. #*'3")*2'%4;)<413:%u%'3%4;-=<"2%a###^^%l’ac*on#ne#sert#qu’à#la#fin#(la#racine)#
@9?)%"$A0-%tour-min7n8%
G0 $1%n#="**'$5"2&%6%)2'%P2%&'%5-*<'M%-4"*$%*'3")*2'*%utilité7n8#
2. #u%Y#[M%a%Y%/"1&%
T0 5")*#=?-J)'#5-1*'#7a’,n’8#&"22:'%5-*%transition7n8%
W0 %$1%4;)<413:%&'%tour-max7n’8%_%u%-4"*$%-]'=3'*%a%Y%a’M%u%Y%)<413:%&'%tour-max7n’8%
5 *'3")*2'%4;)<413:%u%'3%4;-=<"2%a#