deuxieme annee

1
DEUXIEME ANNEE

2
Deuxième Année ISE
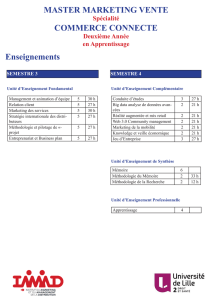
IntitulédesUEetdesenseignementsVolumehoraireCréditsPage
Semestre 3
UE : Mathématiques appliquées 1605 
Optimisation dynamique 302,53
Théorie des jeux 302,54
UE : Statistique mathématique908 
Estimation5045
Théorie des tests4046
UE : Economie 3808 
Economie de l’incertain et de l’information3037
Concurrence imparfaite2028
Comportements macroéconomiques 3039
UE : Statistique 3504 
Analyse descriptive des séries temporelles201,510
Méthodologie d’enquêtes302,511
UE : Sciences sociales403 
Démographie I201,512
Anthropologie économique201,513
UE : Langue et expression 3 502 
Anglais 301‐
Techniques d'expression III 20114
Total semestre37030 
Semestre 4
UE : Econométrie 1907,5 
Econométrie du modèle linéaire 302,515
Econométrie des variables qualitatives302,516
Econométrie des séries temporelles 302,517
UE : Sondages et pratiques des enquêtes 505,5 
Théorie des sondages 30318
Logiciels d’enquêtes201,520
Pratique des enquêtes 1
UE : Economie 4606 
Economie publique20221
Théorie du commerce international20222
Analyse de la pauvreté et des inégalités 20223
UE : Economie 5907 
Macroéconomie dynamique40324
Comptabilité Nationale II30225
Institutions et politique monétaires20226
UE : Informatique 2 302 
Base de données et systèmes d’information 30227
UE : Langue et expression 4 502 
Anglais 301‐
Techniques d'expression IV 20128
Total semestre 37030 
Total 1ère année 74060 

3
Optimisation dynamique
Semestre 3 UE : Mathématique appliquées 1
Volume horaire : 30H Crédits : 2,5
Objectif :
Ce cours est une introduction aux outils de l’optimisation dynamique. L’optimisation dynamique traite des
situations dans lesquelles un agent contrôle l’évolution d’un système, et cherche à optimiser un critère. On
regardera dans un premier temps les problèmes en temps discret, avant d’étudier plus en détail, les problèmes
en temps continu.
Contenu du cours :
I. Programmation dynamique en temps discret
1. Introduction et exemples
2. Horizon fini
- Principe de la programmation dynamique
- Backward induction, stratégie de résolution
3. Horizon infini
- Existence de solutions
- Fonction valeur, équation de Bellman
- Théorèmes de Berge et de Blackwell
- Retour aux politiques optimales
II. Programmation dynamique en temps continu
4. Calcul des variations
- Existence et non-existence
- Equation d’Euler-Lagrange et conditions de transversalité
- Principe de la programmation dynamique
- Equation d’Hamilton-Jacobi
5. Introduction au contrôle optimal
- Principe de Pontriaguine
- Principe de la programmation dynamique
- Equation d’Hamilton-Jacobi-Bellman
- Contrôle en feedback et condition suffisante
Contrôle des connaissances : un examen écrit
Bibliographie :
Demange G. et Rochet J.C (1997), Méthodes mathématiques de la finance, Economica.
Fleming W. et RisheZ R. (1975), Deterministic and stochastic optimal control, Springer Verlag, Berlin.
Lucas R.E et Stockey N.L (1996), Recursive methods in economics dynamics, Harvard University
Press.
Manuelli R.E et Sargent T.J (1987), Exercices in dynamic macroeconomic theory, Harvard University Press.
Mina C. et Gumowski I. (1970), L’optimisation, la théorie, ses problèmes Dunod.
Sargent T. (1987), Macroeconomic theory, Academic Press. Seierstad A. et Sydsaeter (1987), Optimal
control, Theory and Economic applications, North Holland.

4
Théorie des jeux 
Semestre 3 UE : Mathématiques appliquées 1
Volume horaire : 30H Crédits : 2,5
Objectif :
L’objectif de ce cours est de proposer une introduction à la théorie des jeux (non-coopératifs) et à ses
applications économiques. La théorie des jeux (non-coopératifs) est l’étude des décisions optimales
(stratégiques) des agents et de leur interaction dans toute situation impliquant un conflit d’intérêt. Les
concepts et les méthodes de la théorie des jeux sont à la base de développements récents en
économie dans des domaines aussi divers que l’économie publique, l’économie industrielle,
l’économie du travail, la macroéconomie ou l’économie internationale.
Contenu du cours :
I. Introduction : définitions et exemples
II. Jeux statiques à information complète
1. Jeux sous forme normale
2. Elimination successive des stratégies strictement dominées
3. Equilibre de NASH (définition, exemples)
4. Equilibre de NASH en stratégies mixtes
5. Existence de l’équilibre de NASH en stratégies mixtes
6. Multiplicité et sélection des équilibres de NASH
III. Jeux dynamiques à information complète
7. Jeux sous forme extensive
8. Stratégies
9. Equilibre de Nash et menaces non crédibles
10. Un raffinement de l’équilibre de Nash : l’équilibre de Nash parfait en sous jeux
11. Jeux répétés : le « folk theorem »
IV. Jeux statiques à information incomplète
12. Jeux bayésiens et équilibre de Nash bayésien
13. Application : introduction aux enchères
V. Jeux dynamiques à information incomplète
14. Equilibre bayésien parfait
15. Applications : jeux de signal (SPENCE), jeux de réputation
Contrôle des connaissances : un examen écrit
Bibliographie :
Frudenberg D. et Tirole J. (1991), Game theory, Cambridge, Massachusetts: MIT Press.
Demange G. et J.-P. Ponssard (1994), Théorie des jeux et analyse économique, PUF.
Kreps D. (1990), Théorie des jeux et modélisation économique, Dunod.
Myerson R. B. (1991), Game Theory, Analysis of Conflict, Harvard Univ. Press.
Osborne M. J. (2003), An introduction to game theory, Oxford University Press.
Osborne M. J. et A. Rubinstein (1994), A Course in Game Theory, Cambridge, Massachusetts: MIT Press.
Site web: www.gametheory.net

5
Estimation 
Semestre 3 UE : Statistique mathématique
Volume horaire : 50H Crédits : 4
Objectif :
Ce cours doit apporter aux élèves les bases théoriques nécessaires à la construction d’estimateurs à l’intérieur
de modèles probabilistes généraux, ainsi que la compréhension des techniques en aval de la statistique
mathématique (sondages, économétrie, statistique robuste, statistique non paramétrique).
Contenu du cours :
I. Formalisation statistique et information
1. Rappel de Probabilités
- Convergences
- Conditionnement
- Propriétés particulières des vecteurs gaussiens
2. Echantillonnage
- Modèle d’échantillonnage
- Echantillons gaussiens
- Fonction de répartition empirique (statistique d’ordre, quantiles empiriques)
- Tirage d’échantillons fictifs
3. Théorie de la décision
- La décision statistique
- Règle de décision et risque
- Problèmes d’optimalité
- Principes statistiques : BAYES, absence de biais, convergence
4. Exhaustivité et information
- Exhaustivité
- Eléments de théorie de l’information
- Information et exhaustivité
- Théorie de réduction décisionnelle
II. Estimation
1. Estimation Ponctuelle
- Propriétés générales
- Comparaison d’estimateurs : efficacité, optimalité
2. Amélioration d’un estimateur
- Estimation sans biais : inégalité de CRAMER-RAO
- Réduction de la variance : RAO-BLACKWELL
- Réduction du biais : le Jackknife
3. Exemples de modèles exponentiels
- Modèle gaussien
- Théorème de Cochran, de Fisher
4. Méthodes d’estimation
- Le maximum de vraisemblance
- Les méthodes des moindres carrés
- La méthode des moments
- Estimation bayesienne
Contrôle des connaissances : deux examens écrits
Bibliographie :
Gourieroux C. et A. Monfort (1996), Statistique et Modèles Econométriques, Economica
Hoel P.G. (1991), Statistique mathématique, Armand Colin.
Hogg R. V; J. W. McKean; A. T. Craig (2005), Introduction to mathematical statistics, 6 th ed, Pearson.
Monfort A (1997), Cours de Statistique Mathématique, Economica.
Robert C. (1992), L’analyse statistique bayésienne, Economica.
Tassi P. (1989), Méthodes Statistiques, 2 ème ed, Economica.
Zacks S. (1971), The Theory of Statistical Inference, Wiley.
Dagnélie P. (1981), Théorie et méthodes statistiques, Ed. De Gembloux