Télécharger votre série

SERIE N°
MODULATION D’AMPLITUDE
EXERCICE 1
Les ondes électromagnétiques ne peuvent se propager dans l'air sur de grandes distances que dans un domaine de
Fréquences élevées.
Les signaux sonores audibles de faibles fréquences sont convertis en signaux électriques de même fréquence
puis associés à une onde porteuse de haute fréquence afin d'assurer une bonne transmission.
A. La chaîne de transmission
Le document suivant représente la chaîne simplifiée de transmission d'un son par modulation d'amplitude.
Elle est constituée de plusieurs dispositifs électroniques.
1) Parmi les cinq propositions ci-dessous, retrouver le nom des quatre dispositifs électroniques numérotés:
Antenne; Amplificateur HF (Haute Fréquence); Générateur HF (Haute Fréquence) ; Multiplieur ; Voltmètre.
2) Quels sont les signaux obtenus en B, C et D parmi ceux cités ci-dessous?
up(t) = UPmax cos(2πFt).
 Signal, modulant B.F., noté uS(t) + Uo.
 Signal modulé, noté um(t).
3) Le signal électrique recueilli en A à la sortie du microphone correspond à la tension uS(t). Une boîte noire est
intercalée entre les points A et B. Quel est son rôle?
4) Le dispositif électronique 2 effectue une opération mathématique simple qui peut être:
Choisir la bonne réponse sachant que l'expression mathématique du signal obtenu est:
um = k.(Uo + uS(t) ) .UPmax.cos ( 2Ft )
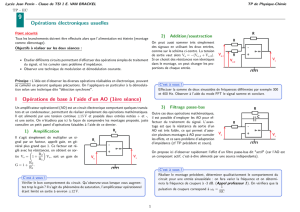
B. La modulation d'amplitude
La voie 1 d'un oscilloscope bicourbe est reliée en B et la voie 2 est reliée en D.
L'oscillogramme obtenu est le suivant:
1) Estimer les valeurs des périodes TS et TP du signal
modulant et de la porteuse.
2) Rappeler l'expression théorique de la fréquence f
en fonction de la période T avec les unités, puis
calculer les fréquences f du signal modulant et F
de la porteuse.
3) L'amplitude de la tension du signal modulé um(t)
varie entre deux valeurs extrêmes, notées
respectivement Um(max) et U m(min)
a- Calculer les valeurs des tensions maximale Um(max)
et minimale U m(min) du signal modulé.
b- En déduire la valeur de m.
c- À quoi correspondrait un taux de modulation m supérieur à 1 ?

4) m s'exprime aussi en fonction de la tension maximale du signal modulant US(max) et la tension Uo
a- Calculer US(max) et Uo. Retrouve-t-on la valeur de m calculée précédemment ?
b- Quelle condition doit-on satisfaire pour obtenir un taux de modulation m < 1 ?
c- Quelle autre condition est nécessaire pour obtenir une bonne modulation ?
d- L'analyse en fréquence du signal montre que celui-ci est composé de trois fréquences f1 ,f2 et f3.
 En fonction de la fréquence du signal modulant f et de la fréquence de la porteuse F, exprimer les fréquences
apparaissant sur le spectre ci-dessous.
EXERCICE 2
2) Préciser pour les signaux ci-dessous celui qui est modulé en amplitude es celui modulé en fréquence tout en justifiant
votre choix.
3
suivant : Avec :
*Uo =5V : tension de décalage .
La tension du signal modulé est de la forme : Us(t)= k[u(t)+Uo].Up(t)
avec : k représente le facteur multiplieur du circuit intégré.
a- Montrer que Us(t) peut se mettre sous la forme :
 A
en fonction de k ,Upm et Uo.
b- Exprimer m en fonction de Um et Uo .Que représente m ?
4) a-  celle ci est la somme de trois fonctions sinusoïdales dont on
exprimera leurs amplitudes en fonction de A et m. On rappelle que : cos a .cos b =1/2[cos (a+b) +cos( a-b)]
b- 
c- 
5) Le spectre du signal AM visualisé sur un analyseur de
spectre est représenté ci-dessous :
a- Quelle est la fréquence Np de la porteuse ?
b- Quelle est la bande de la fréquence du signal ?
6) a- 
b- Quel est la valeur du taux de modulation m ?
c- En déduire la valeur de Um.
EXERCICE 3
Les deux parties a et B sont indépendantes :
Partie A : Etude d’un document scientifique
Le son, la lumière, les images fixes ou mobiles, les textes ou les données peuvent tous être transmis.
Cependant, lorsque la distance devient un facteur important, ces signaux sont trop faibles pour parcourir ne serait-ce
que quelques kilomètres.
se à haute fréquence.
La modulation est une opération essentielle à toute transmission ou diffusion de signaux. Elle se réalise en modifiant
contient
Gilles Willet - Les presses de l’université Laval
Questions :
1- 
2- Citer les deux types de modulation couramment utilisés.
3- 
4- Le véhicule puissant, figurant dans le texte, désigne-t-nature

Partie B : 
on E1 du multiplieur,
on applique une tension uE (t)=u(t)+U0 , avec U0 une tension continue appelée
tension de décalage et u(t)= Um cos(2πNt) une tension sinusoïdale de basse
fréquence NE2 du multiplieur, on applique une tension sinusoïdale
up (t)= Upm cos(2πNpt) de haute fréquence NP .
la tension de sortie est uS (t)=A[1+m cos(2πNt)]cos(2 𝛑𝐍𝐩. t), avec A et m des constantes positives.
USm de us (t) est de la forme : USm = A[1+m.cos(2πNt)].
Y1 la tension u(t) et sur la voie Y2 la tension
US (t). On obtient ainsi les chronogrammes (C1 ) et (C2 ) de la figure 2 
tensions u(t) et us(t).
1) a- 
b- Justifier que uP(t) est la tension porteuse.
2) a- USm )min et maximale (USm )max de la tension de sortie us (t) en fonction de A et m.
b- (USm )min et (USm )max
3) Par exploitation de la figure 2, déterminer les valeurs de :
a- de la fréquence N du signal modulant et celle du signal porteur Np .
b- du taux de modulation m et la valeur de la tension de décalage U0
c- En déduire la valeur de A en précisant son unité.
4) 
correspondant au signal modulé (figure 3).
a- Montrer que la tension de sortie uS 
uS (t) = A [cos(2πNt) + 𝟏𝟐 m .cos(2π(Np-N)t) + 𝟏𝟐 m.cos(2π(Np+N)t)]
b- En déduire les valeurs de N1, N2 , N3 , X1 et X2 .
EXERCICE 4
u1 et u2 -2.
 u1(t)= UO +Um Um
 UO est la tension de décalage
 U2 (t)= UPm NP t) est le signal modulé de fréquence NP UPm
Un dispositif informatisé a permis de visualiser la tension de sortie uS -3.

La tension de sortie s’écrit uS(t) = k.UPm .U0 (1+ UmU0 cos(2πNt)).cos(2πNpt) avec k est une constante positive.
1) 
2) a- Déterminer la fréquence N du signal modulant.
b- Vérifier alors la valeur de la fréquence NP du signal modulé.
3) a- Exprimer le taux de modulation m en fonction de USmmax et USmmin.
b- Calculer la valeur de m et en déduire la qualité de la modulation.
4) a- Montrer que m = 𝑈𝑚
𝑈0
b- Sachant que Um = 4V, calculer U0 .
5) Pour récupérer le signal transmis, on réalise la démodulation du signal de sortie.
a- Quelles sont les deux étapes nécessaires pour effectuer la démodulation ?
b.-Schématiser les deux circuits permettant de réaliser ces deux étapes.
EXERCICE 5
Les trois parties (A), (B) et (C) peuvent traiter indépendantes
A . Les ondes électromagnétiques pour communiquer.
Document texte
L
communication, la voix est convertie en un signal
électrique par un microphone. Grâce à un système de conversion
numérique et de modulation, ce signal électrique est
couplé à une onde porteuse qui, après amplification, est émise
-ci transmet le signal à
téléphonique conventionnelle ou par faisceaux hertziens.
De là sont acheminées les conversations vers le téléphone du destinataire,
selon le même processus, mais en sens inverse (non représenté sur le schéma).
Après démodulation et conversion analogique, le signal électrique est transformé
areil récepteur.
Les ondes électromagnétiques sont déjà très largement utilisées pour la télévision, la radio et les radars, si bien que les
gammes 
915 MHz. Or, un appel nécessite une bande passante de 200 kHz. Autrement dit, dans cette bande de fréquence de
largeurs 25 MHz, on ne devrait pourvoir passer que 125 appels simultanément.
D’après : http://www.linternaute.com/portable/
1) 
2) 
3) a- 
b-  𝜆 dans le vide.
On donne la célérité de la lumière dans le vide c = 3.108 m.s-1
4) a- 
b- 

B. L’émission d’une onde électromagnétique par un portable.
figure 1 :
1) En quel point, A, B, ou C de la figure 1 trouve-t-on :
a- 
b- Le signal modulant ?
2) uP (t) = Upm cos (2πNp.t). Le signal modulant est en
général complexe, mais comme tout signal périodique, il peut se mettre sous la forme : u(t) = Um cos (2πN.t)
a- Pour obtenir une modulation de bonne qualité, faut-il choisir Np très supérieure ou très inférieure à N?
b- 
E1 de ce circuit, le signal modulant u(t)  U0 E2 ,
le signal de la porteuse up (t), et on recueille en sortie le signal modulé, nommé us (t).
Avec : u1 (t) = u(t) + U0 et u2 (t) = up (t)
Sachant que us(t) a pour expression générale :
us(t) = k.u1(t).u2(t), où k est une constante dépendant
uniquement du circuit électronique.
Ecrire us(t) sous la forme : us(t) = Sm cos (2πNp .t)
c- En posant A = k.Upm.U0 et m =
𝑈𝑚
𝑈0
, montré que
Sm peut se mettre sous la forme : Sm N.t).
d- Quelle condition doit remplir m, le taux de modulation, pour que celle-ci soit de bonne qualité?
3) 
us(t) en fonction du temps. Les valeurs numériques ont été choisies pour une lecture
a- Déterminer la fréquence Np de la porteuse, utilisée pour la simulation.
b- Déterminer la fréquence Nm du signal modulant, utilisé pour la simulation.
c- Déterminer Sm max . et Sm min 
déduire le taux de modulation m.