Notes – Didactique et pédagogie mathématiques

Notes – Didactique et pédagogie mathématiques
2016
1
Copyright – Tous droits réservés https://mamanfuturemaitresse.wordpress.com
© Mélodie VERGES
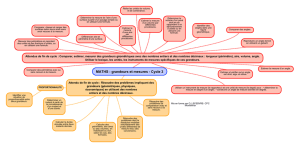
Grandeurs et mesures
Les programmes scolaires
Les activités liées aux grandeurs et à la mesure utilisent des notions géométriques et numériques.
Grandeurs : l’élève doit apprendre à faire la différence entre objet réel ou géométrique, une grandeur associée à cet
objet et la mesure de cette grandeur. Le travail sur les grandeurs précède celui sur la mesure.
Mesure : l’élève doit d’abord s’approprier le concept de grandeur puis mettre en évidence les limites des méthodes
de comparaison pour donner du sens à la notion de mesure.
Travail sur la grandeur  travail sur la mesure à l’aide d’une unité  travail sur la mesure grâce au calcul
Cycle 1 : construire les premiers outils pour structurer sa pensée ; explorer des formes, des grandeurs, des suites
organisées ; observer, trier, distinguer différents types de critères (forme, longueur, masse, contenance…) ; classer
ou ranger des objets selon un critère de longueur/de masse/de contenance.
Cycle 2 : comparer, estimer, mesurer des longueurs/masses/contenances/durées, utiliser le lexique, les unités, les
instruments de mesure spécifiques de ces grandeurs. Comparer des objets et les identifier (masse, contenance,
durée). Estimer des ordres de grandeurs en relation avec les unités métriques, vérifier avec un instrument. Mesurer
avec des instruments adaptés. Encadrer une gr andeur par deux nombres entiers d’unités. Exprimer une mesure
dans une ou plusieurs unités (choisies ou imposées). Comparer/estimer/mesurer des durées. Représenter une
grandeur par une longueur (sur une demi-droite graduée). Résoudre des problèmes de mesurage et de comparaison
en utilisant des opérations. Résoudre des problèmes impliquant des conversions simples d’unités.
Cycle 3 : comparer, estimer, mesurer des grandeurs géométriques avec des nombres entiers et des nombres
décimaux (périmètre, aire, volume, angle). Utiliser le lexique, les unités et les instruments de mesure spécifiques.
Comparer et mesurer des périmètres. Comparer/classer/ranger des surfaces selon leurs aires. Différencier aire et
périmètre. Déterminer/estimer la mesure de l’aire d’une surface par différentes procédures. Relier unités de volume
et de contenance. Déterminer/estimer la mesure d’un volume par différentes procédures. Identifier/comparer/
reproduire des angles dans une figure géométrique. Reconnaître/estimer/vérifier un angle droit/aigu/obtus. Estimer
la mesure d’un angle, utiliser un instrument de mesure et une unité de mesure. Résoudre des problèmes de
comparaison ou utilisant différents unités de mesure ou de conversion. Calculer des périmètres/aires/volumes en
utilisant ou non des formules. Calculer la durée écoulée entre deux instants donnés.
Grandeurs
La grandeur d’un objet est définie par une relation d’égalité qui permet d’établir que deux objets ont la même
grandeur, ou d’inégalité qui permet d’établir qu’un objet est plus grand qu’un autre.
Il est possible de définir plusieurs grandeurs pour un même objet : masse, longueur, volume…
Comparer des angles
Deux angles sont égaux si on peut superposer simultanément leurs sommets et leurs côtés.
Un angle a est plus petit qu’un angle b si, lorsqu’on fait coïncider les sommets de ces deux angles et un de leurs
côtés, alors le second côté de a est inclus dans l’angle de b.
Procédures possibles : utilisation d’un gabarit ; utilisation d’un papier calque
Masse d’un objet
Deux objets ont la même masse si lorsqu’on les pose chacun sur le plateau d’une balance, celle-ci est parfaitement
en équilibre.
Un objet 1 est plus lourd qu’un objet 2 si lorsqu’on les pose chacun sur le plateau d’une balance, un plateau pense
plus d’un côté que de l’autre.

Notes – Didactique et pédagogie mathématiques
2016
2
Copyright – Tous droits réservés https://mamanfuturemaitresse.wordpress.com
© Mélodie VERGES
Longueur d’une ligne
Même longueur : le segment m a la même longueur que le segment n s’il est possible de faire coïncider les
extrémités de ces deux segments. La longueur est la caractéristique de ces segments.
Longueur plus grande que : le segment m a une longueur plus grande que le segment n si lorsqu’on les superpose en
faisant coïncider une de leurs extrémités, la deuxième extrémité de n ne se trouve par sur le segment m.
Ligne brisée/courbe/ouverte/fermée : si l’objet est déployable (ex : fil de fer), sa longueur est obtenue en le
déployant ; si c’est une ligne brisée non déployable, on aligne des segments intermédiaires superposables que lon
aligne bout à bout pour obtenir la longueur de la ligne brisée ; si la ligne est courbe et non déployable, on utilise une
ficelle que l’on superpose en la dépliant et qui donnera la mesure de la longueur.
Procédures pour comparer deux segments sans les mesurer : faire une comparaison directe mentalement (valable
surtout si les longueurs sont très différentes) ; faire coïncider les extrémités de l’objet (si celui-ci est transportable) ;
comparer à l’aide d’un outil intermédiaire (compas, bande de mesure, règle graduée) ; utilisation d’un gabarit ;
utilisation de méthodes de calcul (ex : pour le périmètre d’un carré/rectangle/polygone régulier).
Difficultés : élèves non conservants ; mauvaise manipulation des outils intermédiaires entraînant des problèmes de
précision ; faux théorèmes (ex : la ligne brisée la plus longue est celle qui contient le plus de segments) ; mauvaise
mémorisation du nombre de reports ; mauvaise lecture du résultat (pour l’utilisation d’une règle graduée) ;
difficultés à additionner des mesures complexes (ex : décimales) ; mauvaise mémorisation/utilisation des formules
de calcul ; défaut d’utilisation des unités et de leurs conversions.
Notions transversales : distance entre deux points, hauteur, profondeur, largeur…
Aire d’une surface
L’aire est la grandeur définie pour les surfaces.
Deux aires sont identiques si elles se superposent parfaitement.
Une aire est plus petite qu’une autre si la première est incluse dans la seconde.
Aire d’une surface délimitée par des lignes courbes : le plus simple est d’utiliser un quadrillage (il s’agit alors de
compter les carreaux).
Aire de surfaces non superposables : il faut alors utiliser une surface intermédiaire ou la mesure de ces surfaces.
Procédures pour comparer des aires de surface sans les mesurer : comparaison directe mentalement ; comparaison
à l’aide d’une transformation (ex : découpage/recollement, superposition) ; utilisation de formules de calcul ;
déplacement d’une partie de la figure pour créer une figure usuelle ; utilisation d’un quadrillage ; utiliser des
conversions d’unités d’aires et un tableau de conversion
Difficultés : l’élève mélange aire et encombrement ; l’élève est tenté de ferme la figure si celle-ci est concave ;
difficulté à mobiliser des images mentales ; difficultés de tracés/découpages/recompositions ; problème de
mémorisation des formules de calcul ; erreurs de calculs ; décomposition de la figure géométrique ; difficultés pour
tracer le quadrillage ; difficultés de dénombrement du quadrillage (certains carrés sont coupés par le contour de la
figure) ; mauvaise utilisation du tableau de conversion ; l’élève mélange les conversion de longueur et les
conversions d’aire.
Volume ou contenance d’un solide
Deux solides ont le même volume si, plongés dans une même quantité d’eau dans des récipients identiques, la
hauteur de l'eau monte de la même façon dans les deux récipients.
Un solide 1 a un volume plus grand qu’un solide 2 si, plongés dans une même quantité d’eau dans des récipients
identiques, la hauteur de l'eau monte plus dans un des deux récipients.
Durée
La notion de durée est très abstraite pour les élèves, surtout quand il s’agit de différencier l’horaire et la durée.
Compétences relatives à la durée : savoir lire l’heure en heures et minutes à partir d’un affichage à aiguilles ; savoir
convertir des unités de durée (1 heure = 60 minutes, 1 minutes = 60 secondes) ; savoir résoudre des problèmes liant
horaires et durées ; savoir résoudre des problèmes utilisant des calculs sur des durées.
Procédures utilisables : calcul de proche en proche ; calcul par soustraction
Difficultés : les élèves mélangent les nombres numériques et les unités horaires

Notes – Didactique et pédagogie mathématiques
2016
3
Copyright – Tous droits réservés https://mamanfuturemaitresse.wordpress.com
© Mélodie VERGES
Mesures
La mesure d’une grandeur d’un objet est le nombre d’unités permettant de réaliser une grandeur égale à celle de
l’objet. Conséquences : la mesure est un nombre, elle dépend de l’unité choisie (alors que la grandeur est
invariante). NB : il est possible d’encadrer une mesure (ex : la longueur du segment est comprise entre 3 et 4).
Pour chaque grandeur, le système d’unités de mesure est construit en cohérence avec le système de numération
décimale (ex : un décamètre est une dizaine de mètres ; un kilomètre est un millier de mètres).
Mesure des masses
Pour mesurer des masses on choisit comme unité la masse d’un objet donné ; un instrument est alors nécessaire
(balance à plateaux ou à lecture directe).
Mesurer des longueurs
Pour mesurer des longueurs de segments, on prend un segment quelconque auquel on attribue 1 comme mesure de
sa longueur (on l’appelle alors segment-unité) ; on reporte ensuite ce segment-unité sur le segment que l’on mesure
et on compte le nombre de reports.
Procédures de mesure des longueurs de divers objets : reporter la longueur-unité et compter le nombre de reports ;
utiliser un instrument ; effectuer un calcul.
Mesurer des aires
Pour mesurer l’aire d’une surface, on choisit comme unité l’aire de la surface donnée ; la mesure d’une aire est alors
le nombre d’unités nécessaires pour recouvrir exactement et sans chevauchement la surface en question.
Procédures de mesure des aires en dehors du report de l’unité : avec un quadrillage ; avec un calcul.
Mesure des volumes
Pour mesurer des volumes, on choisit comme unité un solide ; sa mesure est alors le nombre de solides unités
nécessaires pour constituer un solide de même volume (ou le remplir).
Mesure des durées
Evaluer des durées : mesurer un intervalle de temps en choisissant une unité de mesure.
Se repérer dans le temps par rapport à des évènements familiers, par rapport à des repères conventionnels
(calendriers) et en utilisant les nombres.