03. Trigo 3èD

B3
B2
B1
C3
C2
C1
A
CH III Cosinus, sinus et tangente d'un angle aigu d'un triangle rectangle
1. Activité : Découverte des trois nombres
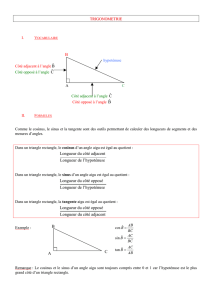
Trois triangles rectangles.
AB
1C1 / AB2C2 / AB3C3
Ils ont en commun le même angle
A
.
Dans ces triangles, le côté le plus long est l'hypoténuse.
Le côté adjacent et le côté opposé sont plus petits
tout en étant proportionnels à l'hypoténuse.
Dans un triangle rectangle,
Le cosinus de
A
est le multiplicateur qui
permet de passer de l'hypoténuse au côté
adjacent à l'angle .
côté adjacent à
A
= hypoténuse x cos
A
0 < cos
A
< 1
Dans un triangle rectangle,
Le sinus de
A
est le multiplicateur qui
permet de passer de l'hypoténuse au côté opposé
à l'angle.
côté opposé à
A
= hypoténuse x sin
A
0 < sin
A
< 1
Dans un triangle rectangle,
La tangente de
A
est le multiplicateur
qui permet de passer du côté adjacent au côté
opposé à l'angle.
côté opposé à
A
= côté adjacent à
A
x tan
A
30°
Hypoténuse
Côté adjacent à
A
AB1 = 3,05
AC1 = 2,65
AC1/AB1 ≈ 0,869
AB2 = 5,15
AC2 = 4,45
AC2/AB2 ≈ 0,864
AB3 = 9,1
AC3 = 7,9
AC3/AB3 ≈ 0,868
x cos 30° ≈ 0,866
Hypoténuse
Côté opposé à
A
AB1 = 3,05
B1C1 = 1,5
B1C1/AB1 ≈ 0,491
AB2 = 5,15
B2C2 = 2,55
B2C2/AB2 ≈ 0,495
AB3 = 9,1
B3C3 = 4,55
B3C3/AB3 = 0,5
x sin 30° = 0,5
C. adjacent à
A
C. opposé à
A
AC1 = 2,65
B1C1 = 1,5
B1C1/AC1 ≈ 0,566
AC2 = 4,45
B2C2 = 2,55
B2C2/AC2 ≈ 0,573
AC3 = 7,9
B3C3 = 4,55
B3C3/AB3 ≈ 0,576
x tan 30° ≈ 0,577

2. Ce que je dois retenir.
A) Connaître les côtés
B) Connaître les formules trigonométriques
C) Remarques
1. Cosinus, sinus et tangente sont des nombres sans unité.
2. Le cosinus et le sinus sont des nombres inférieurs à 1.
3. La tangente est un nombre qui peut être plus grand que 1.
D) Calculatrice
Vérifier d'abord que la calculatrice est en mode " degré "
cos 20° ≈ 0,94 cos 60° = 0,5 sin 45° ≈ 0,71 tan 62° ≈ 1,89
côté adjacent à
A
= hypoténuse x cos
A
côté opposé à
A
= hypoténuse x sin
A
côté opposé à
A
= côté adjacent à
A
x tan
A
côté opposé à
A
côté adjacent à
A
hypoténuse
A
C
B
■
côté adjacent
ˆ
B
côté opposé à
ˆ
B
hypoténuse
A
B
C
■
côté opposé à
A
hypoténuse
A
C
B
■
côté adjacent à
A

3. Savoir calculer un côté.
A) On connaît 2 côtés du triangle
Exemple
Le triangle EFG est rectangle en E. Appliquons le théorème de Pythagore
!!GF2 = EG2 + EF2
5,42 = EG2 + 52
29,16 = EG
2 + 25
EG
2 = 29,16 – 25
EG =
4,16
(cm) valeur exacte
EG ≈ 2,0 (cm) arrondi au dixième
B) On connaît un côté et un angle
Exemple 1
Le triangle RST est rectangle en S. Utilisons la trigonométrie.
• Je cherche [RS] : c'est le côté adjacent à l'angle
R
. Je connais l'hypoténuse.
RS = RT x cos
R
RS = 5,2 x cos 28°
RS ≈ 4,6 (cm)
• Je cherche [TS] : c'est le côté opposé à l'angle
R
. Je connais l'hypoténuse.
TS = RT x sin
R
TS = 5,2 x sin 28°
TS ≈ 2,4 (cm)
Exemple 2
Le triangle ABC est rectangle en B. Utilisons la trigonométrie.
• Je cherche [AC] : c'est l'hypoténuse. Je connais le côté adjacent.
AC =
AB
cos A
AC =
5
cos32°
AC ≈ 5,9 (cm)
• Je cherche [BC] : c'est le côté opposé. Je connais le côté adjacent.
BC = AB x tan
A
BC = 5 x tan 32°
BC ≈ 3,1 (cm)
?
4,75 2,85
7,6
5,7
5,13
EF
G
5,4 cm
5 cm
?
5,7
RS
T
28°
5,2 cm
?
4,75
AB
C
5 cm
32°
?
?

3. Savoir calculer un angle dans un triangle rectangle.
A) On connaît l’autre angle aigu
Le triangle RTS rectangle en R donc les angles aigus
ˆ
R
et
ˆ
T
sont complémentaires.
ˆ
R
+
ˆ
T
= 90°
ˆ
T
= 90 –
ˆ
R
ˆ
T
= 90° – 28°
ˆ
T
= 62°
B) On connaît deux côtés
Exemple 1
Le triangle EGF est rectangle en E. Utilisons la trigonométrie.
Je connais [EF] : c'est le côté opposé.
Je connais [EG] : c'est le côté adjacent.
EF = EG x tan
G
tan
G
=
EF
EG
tan
ˆ
G
=
5
3
ˆ
G
= tan–1 (
5
3
)
ˆ
G
≈ 59°
Exemple 2
Le triangle EGF est rectangle en E. Utilisons la trigonométrie.
Je connais [EF] : c'est le côté opposé.
Je connais [FG] : c'est l'hypoténuse.
EF = EG x sin
G
sin
G
=
EF
EG
sin
G
=
5
5, 4
ˆ
G
= sin–1 (
5
5, 4
)
ˆ
G
≈ 68°
tan–1
on utilise la touche pour trouver l'angle.
sin–1
on utilise la touche pour trouver l'angle.
?
4,75 2,85
7,6
5,7
5,13
EF
G
5,4 cm
5 cm
4,75 2,85
EF
G
5 cm
3 cm
?
5,7
RS
T
28°
?

4. Trouver une démarche pour aboutir à un résultat
Démarche
L'augmentation est égale à EC – IC
• On calcule IC (dans le triangle rectangle IHC où on connaît 2 mesures)
• On calcule EC (dans le triangle rectangle EHC)
— On calcule d'abord HC pour avoir une 2ème mesure dans le triangle EHC
— On calcule EC
• On calcule de combien on rallonge la laisse.
Conclusion : 4 étapes
Rédaction
Etape 1 : Je calcule IC
Le triangle IHC est rectangle en H.
On cherche IC, l'hypoténuse et on connaît IH, le côté opposé à l'angle de 40°.
IC =
IH
sin C
IC =
6
sin 40°
IC ≈ 9,3 (m)
Etape 2 : Je calcule HC
Je cherche HC qui est le côté adjacent à l'angle de 40°. Je connais le côté opposé IH.
HC =
IH
tan C
HC =
6
tan 40°
HC ≈ 7,2 (m)
Etape 3 : Je calcule IC.
Le triangle CEH est rectangle en H.
Je cherche EC qui est l'hypoténuse. Je connais les deux autres côtés EH et CH.
Selon le théorème de Pythagore :
EC
2 = EH2 + HC2
EC
2 = (3 + 6)2 + (
6
tan 40°
)2
Un propriétaire a un chien attaché au piquet planté en C.
La longueur initiale CI de la laisse permet au chien
d'atteindre le début du portail, au point I lorsque la laisse
est tendue.
Pour une meilleure surveillance de l'entrée, le propriétaire
aimerait que son chien puisse atteindre le portail à l'autre
bout soit au point E.
De quelle longueur minimale le propriétaire doit-il
rallonger la laisse de son chien ?