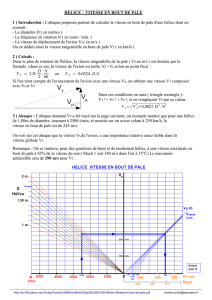
Modélisation d`un rotor éolien HAWT par la méthode Elément de

___________________________________________________________________________________________________
9ième Congrès de Mécanique, FS Semlalia, Marrakech 280
Modélisation d’un rotor éolien HAWT par la méthode
Elément de pale/Quantité de mouvement.
R. DIZENE 1, N. AMROUCHE 1 R. GHOUBALI 1 et S.
HAINE1
Laboratoire de Mécanique Avancée
Faculté de Génie Mécanique et Génie des Procédés
Université USTHB
BP 32, El Alia 16111 Bab Ezzouar Alger
E-mail : [email protected]
I-Introduction :
Dans la conception d’une éolienne, le rotor est certainement
l’un des éléments les plus essentiels. En effet, il s’agit d’un
ensemble tournant, éventuellement de grande dimension,
qui peut être amené à fonctionner pendant plus de vingt ans
dans un environnement aérodynamique souvent perturbé et
engendrant des contraintes de « fatigue » quelques fois
importantes, dans un environnement climatique sévère. A
partir de ce constat, le rapprochement avec les rotors
d’hélicoptères devient évident. C’est pour cette raison que
les machines les plus répondues actuellement sont les
machines munies de rotor à axe horizontal, parallèles à la
direction du vent (bipales ou tripales). Leur conception
aérodynamique a beaucoup profité de l’essor technologique
aéronautique d’hélicoptères surtout en ce qui concerne la
forme aérodynamique des pales et des matériaux
composites utilisés. Ainsi, l’apport particulièrement
important de l’industrie aéronautique et même spatiale peut
constituer une aide efficace au profit des applications très
diverses. Cette contribution concerne l’expérience acquise
sur le plan des connaissances de base et des moyens de
calcul.
Les méthodes appliquées et les principes de fonctionnement
des rotors des éoliennes sont inspirés de ceux des hélices et
des rotors d’hélicoptère. Différentes approches ont été
utilisées. Nous citerons par exemple la théorie classique du
moment axial généralement appliquée pour une étude
préliminaire ou simplifiée : la théorie des cascades [1].
Particulièrement adaptée aux éoliennes lentes, la théorie de
la ligne portante [2,3] ou la théorie de la surface portante
[4] qui permettent une évaluation plus précise des
performances aérodynamiques des rotors éoliens. Dans
notre cas, le modèle retenu est basé sur la méthode
tourbillonnaire qui consiste à combiner la théorie de l’aile
portante avec la loi de la conservation de la quantité de
mouvement [5].
Un certain nombre de chercheurs ont conçu des méthodes
pour prévoir les performances des rotors des éoliennes.
L’analyse classique des éoliennes a été à l’origine
développée par Betz et Glauret (Glauret, 1935) dans les
années trente. Plus tard, ces théories ont été développées et
adaptées pour des résolutions numériques [6]. Dans ces
méthodes, la théorie de quantité de mouvement et de
l’élément de pale sont combinés dans une seule théorie qui
permet le calcul des caractéristiques d’une section annulaire
du rotor. Les caractéristiques pour le rotor entier sont alors
obtenues par l’intégration, ou l’addition des valeurs
obtenues pour chacune des sections annulaires. Dans la
littérature cette méthode se présente sous différentes
appellations : méthode Glauert, méthode tourbillonnaire,…;
mais pour notre cas nous avons retenu le nom suivant :
« méthode de l’élément de pale /quantité de mouvement ».
II-Analyse physique:
Généralement, les performances aérodynamiques des
profils d’ailes des rotors éoliens à axes horizontal (HAWT)
sont évaluées numériquement par deux méthodes : la
méthode de l’écoulement potentiel/couche limite [7] et la
méthode basées sur la résolution des équations de Navier
stokes CFD [8]. L’écoulement autour d’un profil est dit
attaché si l’écoulement couvre la surface du profil du bord
d’attaque au bord de fuite, toutefois si l’angle d’attaque
excède une certaine valeur alors on remarque que
l’écoulement ne peut plus atteindre le bord de fuite et
décroche de la surface du profil sur une ligne de
décollement. Dans cette région la direction de l’écoulement
est inversée et on parle alors d’écoulement de retour,
provoquant une forte décroissance de la portance et une
forte augmentation de la traînée, donc le profil de la pale du
rotor ne peut plus tirer assez d’énergie de l’écoulement.
C'est le phénomène de décrochage utilisé pour la régulation
de puissance.
L’angle d’attaque de l’écoulement incident par rapport à la
pale est déterminé par la vitesse de la pale du rotor et la
vitesse du vent mais puisque les pales régulées par
décrochage n’opèrent qu’à vitesse de rotation constante, la
variation de cet angle ne dépendra théoriquement que de la
vitesse du vent. L’art dans la conception des pales à
régulation passive réside donc dans sa faculté á permettre
un décrochage graduel le long de l’axe longitudinal de la
pale et ainsi maintenir un puissance constante pour une très
large gamme de vitesse. Mais en réalité le comportement du
phénomène de décrochage est beaucoup plus compliqué et
difficile à cerner car il met en jeux l’influence du caractère
instationnaire et tridimensionnel de l’écoulement.
La régulation par décrochage aérodynamique a avant tout
l'avantage d'éviter l'installation de pièces mobiles dans le
rotor, ainsi qu'un système de contrôle complexe et onéreux.
L'inconvénient d’une telle régulation se pose donc au
niveau des grands défis qu’elle lance à la conception
aérodynamique des pales, mais également à la conception
de l'éolienne entière soumise à des vibrations causées par
des variations instantanées des charges aérodynamiques
induites par le phénomène de décrochage. Actuellement
environ deux tiers des éoliennes qui sont installées dans le
monde le sont à pas fixe. Les modèles existants et utilisés

___________________________________________________________________________________________________
9ième Congrès de Mécanique, FS Semlalia, Marrakech 281
jusqu’à maintenant pour le design et la conception des pales
sont basés sur des approches simplifiées, tel que le concept
du disque actuateur et la théorie de l’élément de
pale/quantité de mouvement. Comme ces modèles s’avèrent
limités à des écoulements stationnaires et uniformes dont la
présente étude en est un, nous avons opté pour la méthode
de l’élément de pale/quantité de mouvement.
III- Formulation mathématique :
La méthode de l’élément de pale/quantité de mouvement
présente certes quelques insuffisances qui peuvent être
résorbées en tenant compte des trois considérations : les
pertes aux extrémités de la pale, l’état de freinage et l’effet
du gradient de vent.
Figure 1 : les caractéristiques géométriques de la pale
[9]
Ces pertes causent une diminution du coefficient de couple
aux extrémités, et par conséquent, une diminution du
coefficient de puissance. Pour remédier à ces pertes, on
utilise un modèle afin de déterminer un coefficient de
correction à chaque extrémité. Le modèle de Prandtl nous
donne le facteur de perte au bout de la pale. Notre méthode
reste efficace pour des valeurs de a inférieures à 0.5.
Lorsque l’on dépasse cette valeur l’écoulement loin dans le
sillage a tendance à se renverser et s’approche du rotor à
partir de l’aval. Ce phénomène s’appelle l’état de freinage,
et qui implique de fortes interactions visqueuses. Les rotors
éoliens sont exposés à des gradients de vent dus à la couche
limite atmosphérique. Ceci peut influencer les
performances de l’élément de pale au cours de sa rotation.
Coefficients de portance CL et de trainée CD :
D
cos et C sin
L N N
C C C
α α
= =
avec
1
min ,
0,283
0,222 sin
N
C G
α
=
+
Equation du facteur d’interférence des vitesses :
( )
22
2
1 cos
1 1 cos
2 sin
2
L
aC
a
F
ψ
σ
ϕ
ψ
−
− −
=
cos
'
1 ' 8cos
L
C
Faa
σ ψ
ϕ
=
+
Equation de l’état du freinage avancé :
2
cos²
4 (1 ) (1 ) cos
2 sin²
L
aF aF C a
σ ψ
ϕ
ϕ
− = −
0143 0.0203 0.6427(0.889 )
H
C
aF
+ − −
=
Avec :
2 2
0.889 0.44 1.55
H
C a a F
= − +
Equation d’effet du gradient des vents :
1 cos
E
Lcône
r
V V H
θ
∞
= +
Avec :
cos
Locale cône
H H r
θ
= +
IV- Résultats et Discussions:
La méthode dite de élément de pale /quantité de
mouvement ou BEM fût et reste un outil d’estimation et de
prédiction des performances des rotors éoliens, ou le rotor
est plongé dans des écoulements instationnaires. Dans le
cas des turbines éoliennes, ces instabilités sont le résultat de
la turbulence atmosphérique, les cisaillements du vent, les
frontières du sol et des reliefs, etc.........Les caractéristiques
aérodynamiques et les paramètres de performances sont
affectés tant qu’ils dépendent de la fréquence de ces
variations, de leur amplitude et du point de fonctionnement.
D’autres facteurs qui affectent le phénomène de décrochage
dynamique sont les nombres de Mach et de Reynolds ainsi
que la forme géométrique du profil de la pale utilisée. La
discussion de nos résultats qui va suivre est basée sur les
considérations de ce phénomène lorsque le rotor est soumis
à des variations du nombre de Reynolds, de l’angle
d’attaque et de la forme géométrique du profil.
On présente les performances aérodynamiques à savoir les
coefficients de couple, de poussée et de puissance d’un
rotor éolienne à axe horizontal en utilisant la méthode de
l’élément de pale quantité de mouvement. Un algorithme,
largement inspiré du fameux code de calcul PROP résultat
du travail de Wilson et Lissman [6], est mis en place pour
pouvoir estimer ces coefficients, en tenant compte de la
variation du profil et du nombre de Reynolds le long de la
pale, ainsi que le nombre de pales et l’angle de calage. La
simulation concerne le calcul des coefficients de portance et
de traînée à différents angles d’attaque, des profils
aérodynamiques les plus répondus dans l’industrie des
rotors éoliens ; le NACA4412.
Une partie des résultas de notre procédure d’analyse et la
discussion des performances du rotor est la détermination
des caractéristiques aérodynamiques représentées par les
coefficients de portance CL et de traînée CD de chaque
élément de pale en fonction de l’angle d’attaque local. Ces
résultats sont donc montrés sur les figures 2 et 3 et illustrent

___________________________________________________________________________________________________
9ième Congrès de Mécanique, FS Semlalia, Marrakech 282
les évolutions des coefficients CL et CD en fonction de
l’angle d’attaque alpha (α) dont la plage de valeurs varie en
général de -15 degrés à +25 degrés, selon la disponibilité
des données expérimentales. Les courbes obtenues sont
présentées pour le profil d’ailes testé ; à savoir le NACA
4412.
0 5 10 15
0,0
0,2
0,4
0,6
0,8
1,0
1,2
1,4
1,6
1,8
2,0
CL
Alpha (°)
Calcul XFLR5
Expérience [41]
NACA 4412
Re=83000
Figure 2 : Caractéristiques aérodynamiques du profil
NACA4412 ; Re =83000
Vitesse du vent =8.13 m/s
L’examen des courbes caractéristiques observé dans le cas
du profil NACA 4412 (Figure2 et 3), montre une évolution
globale semblable : un accroissement progressif du
coefficient CL avec l’angle d’attaque α ; alors que le
coefficient CD diminue, passe par un palier constant puis
augmente avec l’angle α. Ce comportement est d’ailleurs
confirmé par la comparaison avec les courbes
expérimentales. Toutefois, la comparaison des profils fait
ressortir des écarts de valeurs entre celles calculées dans la
présente étude et celles mesurées. Ces différences sont plus
marquées à faible nombre de Reynolds qu’elles ne le sont à
nombre de Reynolds élevé. L’observation la plus frappante
concernant ces écarts est notée entre α=8 degrés et α=15
degrés et plus, où l’on estime des valeurs différentielles
maximales de l’ordre de 20% pour CL et 70% pour le CD à
des valeurs de α comprises entre 10 degrés et 15 degrés.
On constate aussi que ces écarts relevés sur les courbes
comparés montrent que le coefficient de portance CL est
surestimé par le calcul alors que le coefficient de traînée
CD est sous estimé par le calcul.
Ces constations peuvent s’expliquer à l’aide de plusieurs
causes : la première de ces causes est le principe même de
la méthode BEM qui considère des traitements isolés de
chaque élément de pale. De ce fait, les forces de portance et
de traînée tendent à être parfaites et comme les deux
phénomènes s’inversent physiquement ceci explique cela.
V-Conclusion :
La comparaison avec l’expérience des résultats de calcul du
coefficient de puissance montre une concordance
acceptable, qui se traduit par une surestimation de l’ordre
de 13,5% de la puissance extraite du vent pour une vitesse
spécifique λ égale à 5.Afin de confirmer l’intérêt de l’angle
de calage sur la puissance du rotor, une variation de cet
angle montre que le couple de démarrage est nettement
amélioré à la valeur de 4 degrés .Au delà, les performances
ne conviennent pas pour un bon fonctionnement du rotor.
Finalement, l’influence de la forme du profil montre et
confirme des résultats précédents, à savoir que le profil
NACA 4412 présente, d’une manière générale, les
meilleurs performances obtenues.
-5 0 5 10 15 20
0,00
0,02
0,04
0,06
0,08
0,10
CD
Angle d'attaque (°)
Calcul XFLR
Expérience [41]
NACA 4412
Re = 83000
Figure 3 : Caractéristiques aérodynamiques du profil
NACA4412 ; Re =83000
Vitesse du vent =11.76 m/s
REFERENCES :
[1] M.Q.Islam “A theoretical investigation of the design of
horizontal- axis wind turbines“, Thèse de Doctorat,
Université de Brussel (1986)
[2] M.B.Anderson, “A vortex-wake analysis of horizontal-
axis wind turbine and a comparison with a
modified blade-element theory “, third international
symposium on wind energy systems, Denmark
(1980).
[3] J. Hernadez and A. Cresp, “Aerodynamic Calculation of
the Performance of Horizontal Axis Wind Turbines
and comparison with Experimental Results”, Wind
Engineering Vol.11, N° 4,pp.77-187(1987)
[4] S.Lain, J.A.Garcia and R.Aliod, ”Development of a
lifting surface 2D panal method to computer the
three dimensional pressure distribution over the
blade of a horizontal axis wind turbine” , Wind
Engineering Vol. 16, N°2,pp21-40(1993)
[5] Yves Mercadier ”Méthode de calcul dela géométrie et
des performances d’une helice éolienne rapide”,
Journal of Wind Engineering Vol.2, N°1(1978).
[6] R.E. Wilson, PBBS.Lissaman and S.N. Walker,
“Aerodynamic Performance of Wind Turbines”,
Oregan State University (1976)
[7] K.Ameur & O.Guerri, “ Caractérisation des profiles
d’aile utilisés dans les rotors Eoliens à l’aide du code
Xfoil “6eme séminaire International sur la Physique
Energétique, Béchar (Oct.2002).
[8] C.Bak, P.Fulgsnag, N.N.Sorensen, H.A. Madsen,
W.Z.shen and J.N Sorensen” Airfoil Characteristics
for wind Turbines”, RisO-R-1065( EN), RisO
National Laboratory, Roskide, Denmark (Mar.1999)
[9] K. Ameur « Etude numérique des performances
aérodynamiques des rotors à axe horizontal