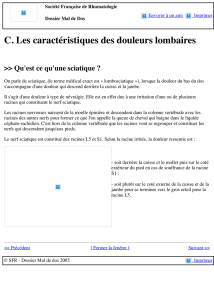
On considère un entier n vérifiant n 2. Définition 1 On appelle racine

ECS1-1 Lycée Pierre de Fermat
2016-2017
Sur les racines de l’unité
On considère un entier nvérifiant nÊ2.
Définition 1
On appelle racine n-ième de l’unité tout nombre complexe z∈ vérifiant
zn=1.
Pour n=2, les racines carrées de l’unité sont 1 et −1.
Cherchons maintenant les racines n-ièmes de l’unité avec nÊ1 quelconque.
Soit z=ρ e
iθ
un nombre complexe non nul écrit sous forme trigonométrique (i.e.
ρ∈∗
+et θ∈), alors :
zn=1⇐⇒ ρneinθ=ei×0
⇐⇒ ρn=1 et nθ≡0 [2π]
⇐⇒ ρ=1 et : ∃k∈/nθ=2kπ
⇐⇒ ρ=1 et : ∃k∈/θ=2kπ
n
⇐⇒ ∃k∈/z=e2ikπ
n
⇐⇒ ∃k∈ 0,n−1/z=e2ikπ
n.
Théorème 2
Les racines n-ièmes de l’unité sont les nnombres complexes :
1,ω,ω2,...,ωn−1avec ω=e2iπ
n.
Exemples
1Ï Les racines cubiques (i.e. 3
e
) de
l’unité sont :
1 , ei2π
3et ¡ei2π 3¢2=ei4π 3
c’est-à-dire i.e. en notant j =e2iπ
3:
1 , j et j2.
•1
•
e2iπ
3
•
e4iπ
3
2ÏLes racines 4ede l’unité sont :
1 , ei2π
4=eiπ 2,¡ei2π 4¢2=eiπet ¡ei2π 4¢3=ei3π 2
c’est-à-dire :
1 , i , −1 et −i.
•1 •
−1
•
i
•
−i
3ÏLes racines 5ede l’unité sont :
1 , ei2π
5,¡ei2π 5¢2=ei4π 5,¡ei2π 5¢3=ei6π 5,
et ¡ei2π
5¢4=ei8π 5.
•1
•
e2iπ
5
•
e4iπ
5
•
e6iπ
5
•
e8iπ
5
Remarques
1ÏSi zest une racine n-ième de l’unité alors c’est aussi le cas de z.
En fait, si z=ωkalors z=ωn−k.

2Ï Le produit de deux racines n -ièmes de l’unité est encore une racine n -ième
de l’unité.
3ÏInterprétation géométrique :
Comme on l’a constaté sur les
exemples, les points du plan com-
plexe dont les affixes sont les racines
n -ièmes de l’unité sont situés sur
le cercle trigonométrique et sont les
sommets d’un polygone régulier à n
cotés.
Pour n= 6 on obtient donc un hexa-
gone régulier :
•1
•
e2iπ
3
•
e4iπ
3
•
−1
•
eiπ
3
•
e5iπ
3
On termine avec un résultat à retenir : la somme de toutes les racines n -ièmes de
l’unité est nulle!
Proposition 3
On pose ω=ei2π
nalors :
1+ω+ω2+ · · · + ωn−1=0.
Démonstration
Comme ω6= 1, on a :
1+ω+ω2+ · · · + ωn−1=1−ωn
1−ω
d’où le résultat puisque ωn=1.
Par exemple, on a 1 +j+j2=0.