DS 7 – Cinématique et dynamique newtoniennes

Exercice 1 : Saut en parachute 15 pts
Afin d’expérimenter les mouvements de chute verticale, la courageuse Marinella n’hésite pas à
effectuer un saut en parachute. Elle saute donc d’un hélicoptère en vol stationnaire. Sa vitesse
initiale est donc nulle.
On considérera sa chute parfaitement verticale sans présence de vent pouvant dévier sa chute. Elle
commence donc en chute libre puis finit par ouvrir son parachute.
L’air exerce des frottements, parachute ouvert ou pas. Les forces de frottements sont d’autant plus
grandes que la vitesse est grande. Autrement dit, les forces de frottements sont proportionnelles à
la vitesse. On néglige une éventuelle poussée d’Archimède.
Le graphe ci-dessous donne l’évolution de la vitesse de Marinella et de son matériel au cours du
temps où l’on distingue 5 phases du mouvement.
1.1 Dans quel référentiel le mouvement de Marinella est-il décrit ? ❶ Référentiel terrestre.
1.2 Ce référentiel est-il galiléen ? Justifier. ❶ Oui car compte-tenu de la durée de l’expérience (moins d’une minute), on
peut considérer que ce référentiel vérifie lui-même le principe d’inertie.
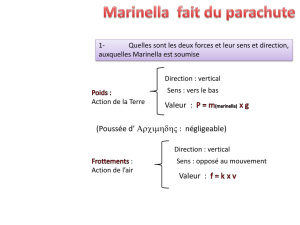
1.3 Quelles sont les deux forces auxquelles Marinella est soumise ? Les représenter sur un schéma. ❷
Voir schéma plus haut : il y a le poids et les frottements de l’air
1.4 Donner les caractéristiques de ces deux forces (sens, direction, norme, point d’application). ❶
Force Poids : P Frottements de l’air : F
Direction Verticale Verticale
Sens Vers le bas Vers le haut
Norme (valeur) P=m.g F
NOM Prénom : Classe : TS Durée : 1h
Appréciation
:
/30
DS 7 – Cinématique et dynamique newtoniennes Date :
⃗
⃗

1.5 A l’aide du graphe, trouver la durée de chaque phase. ❷ ½
Voir tableau ci-dessous
1.6 Indiquer pour chaque phase comment varie la vitesse. ❷ ½
Voir tableau ci-dessous
1.7 Indiquer pour chaque phase comment varie l’accélération. ❷ ½
Voir tableau ci-dessous
1.8 A l’aide de la 2nde loi de Newton, interpréter ces variations de vitesse et d’accélération pour chaque phase. ❷ ½
Phase Durée
Variation de la
vitesse
Variation de
l’accélération Interprétation (2ème loi de Newton)
1 1 s Augmente
linéairement Constante
On remarque que v = a x t (fonction linéaire)
Donc  = 
 = 
Or d’après la 2ème loi de Newton
⃗= .⃗ ↔  ⃗= 
⃗
Au début de la chute, la vitesse étant faible, on peut négliger
les frottements de l’air, ne reste à considérer que le poids.
Il vient alors : a = g
2 14 s Augmente Diminue
Il faut considérer les deux forces.
⃗
+
⃗=∑ ⃗= .⃗ ≠ 0
⃗
avec P > Fair
Donc ∑
⃗ dirigée vers le bas, c’est-à-dire dans le sens du
mouvement.
La vitesse continue d’augmenter mais moins vite à cause des
frottements de l’air sur Marinella.
L’accélération diminue car les frottements deviennent de plus
en plus importants (ils dépendent de la vitesse).
3 5 s Constante Nulle
On a
⃗
=
0
⃗
et logiquement
⃗
=
⃗
C’est un mouvement de translation rectiligne uniforme
Comme ∑
⃗= .⃗ = 0
⃗
Cela signifie que les forces se compensent.
4 4 s Diminue Diminue
Marinella ouvre son parachute
, donc les forces de frottements
deviennent encore plus grandes. La vitesse diminue
brutalement.
5 + de 6 s Constante Nulle
On a
⃗
=
0
⃗
et logiquement
⃗
=
⃗
C’est un mouvement de translation rectiligne uniforme
Comme
∑
⃗
=
.
⃗
=
0
⃗
Cela signifie que les forces se compensent.

Exercice 2 : Tir sportif 15 pts
Après le parachute, Marinella s’attaque au biathlon. Le biathlon est une épreuve sportive combinant ski de fond et tir à la
carabine. On étudie un aspect du parcours de Marinella de masse M=75,0 kg portant une carabine de masse mc = 4,0 kg.
Lors du tir, une balle de masse mb=5,0 g est expulsée de la carabine avec une vitesse vb=310 m.s-1. La balle doit atteindre
l’une des cinq cibles disposées sur un support.
2.1 Calculer la quantité de mouvement de la balle à la sortie du canon. ❶
= .=5,0.10-3 x 310 = 1,6 kg.m.s-1
2.2 Calculer l’énergie cinétique de la balle à la sortie de la carabine. ❶
=1
2.
=1
2×5,0.10 ×310= 2,4.10
2.3 Comment peut-on déterminer la vitesse de recul 
⃗
de la carabine ? On ne tiendra pas compte des gaz éjectés. ❶
En appliquant la conservation de la quantité de mouvement. Pour cela on suppose le système {carabine + balle} isolé.
Ce qui semble être le cas puisqu’ils sont immobiles dans le référentiel terrestre.
2.4 Calculer la valeur de vc dans le cas où le système étudié est constitué de la carabine et de la balle, système supposé
isolé avant et après le tir. ❸
Avant le tir, le système est immobile donc 
⃗
= 0
⃗
Après le tir, la quantité de mouvement du système est égale à la somme des quantités de mouvement de la carabine et de
la balle. Soit : 
⃗
= 
⃗
+
⃗
Le principe de conservation de la quantité de mouvement s’écrit ici : 
⃗
= 
⃗
Autrement dit : 
⃗
+
⃗
= 0
⃗
Ou encore 
⃗
= −
⃗
On en déduit que 
⃗
= −
⃗
cela signifie que la vitesse de la carabine a la même direction mais un sens opposé à la
vitesse de la balle.
D’où =.
=,.× , = 0,39 .
2.5 En réalité, l’athlète tient fermement la carabine en appui sur son épaule. Quel système faut-il considéré dans ce cas ? ❶
Dans ce cas il faut considérer le système {athlète + carabine + balle}
La balle arrive à la vitesse horizontale ⃗ de valeur v = 300 m/s sur l’une des cinq cibles
noires. Sous l’impact de la balle, la cible noire, de masse m = 60 g, se déplace puis active
un mécanisme qui fait basculer un cache blanc devant la cible. Le tireur sait ainsi qu’il a
réussi son tir.
2.6 Pour quelle raison la vitesse de la balle est-elle plus faible lorsqu’elle arrive sur la
cible alors qu’elle possédait une vitesse plus grande juste après avoir été expulsée
de la carabine ? ❶ A cause des frottements de l’air.
2.7 En supposant isolé le système constitué par la cible noire et la balle incrustée,
exprimer sa quantité de mouvement 
⃗
avant l’impact puis exprimer 
⃗
après
l’impact. Que peut-on dire de 
⃗
et 
⃗
. Justifier. ❸
Avant l’impact : 
⃗
= ⃗
Après l’impact : 
⃗
= (+ )
⃗
Le système est supposé isolé donc la quantité de mouvement est conservée : 
⃗
= 
⃗
2.8 En déduire l’expression de la vitesse du système {cible noire + balle incrustée} après l’impact et la calculer. ❷
La conservation de la quantité de mouvement s’écrit alors : ⃗ = (+ )
⃗
Soit  = .
 =,. × ,.  . = 23 .
2.9 Calculer l’énergie cinétique de ce système. ❷
=
(+ ).
=
×(5,0+60).10 ×23= 17 J