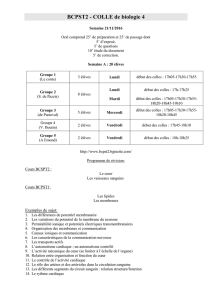
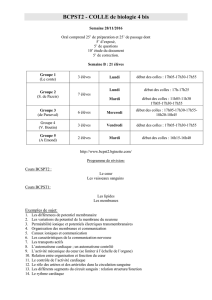
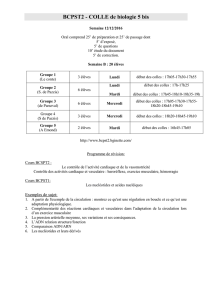
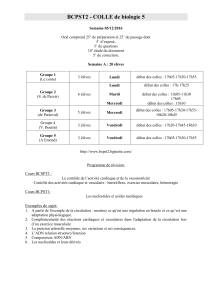
Semaine 3

C→C∗
z7→ exp(z)
x3y0−x2y= 1
z∈CSn(z) = nzn−1+ (n−1)zn−2+· · · + 3z2+ 2z+ 1 z= 1 z6= 1 z6= 1
(1 −z)Sn(z)
n−1
k=1
ksin 2kπ
n.
xy0+ (x−1)y=x2
x6=π
2+kπ k ∈Z
Sn(x) =
n−1
k=0
cos(kx)
(cos(x))k.
(2 + x)y0= 2 −y
z, z0∈C1zz06=−1
z+z0
1 + zz0∈R.
C→C∗
z7→ exp(z)
x3y0−x2y= 1
z∈CSn(z) = nzn−1+ (n−1)zn−2+· · · + 3z2+ 2z+ 1 z= 1 z6= 1 z6= 1
(1 −z)Sn(z)
n−1
k=1
ksin 2kπ
n.
xy0+ (x−1)y=x2
x6=π
2+kπ k ∈Z
Sn(x) =
n−1
k=0
cos(kx)
(cos(x))k.
(2 + x)y0= 2 −y
z, z0∈C1zz06=−1
z+z0
1 + zz0∈R.