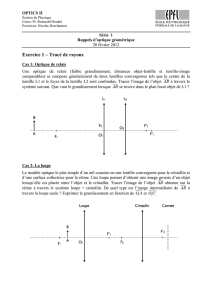
Exercice 1 – Tracé de rayons Cas 1 : Optique de relais Cas 2 : La

OPTICS II
Section de Physique
Cours: Pr. Romuald Houdré
Exercices: Nicolas Descharmes
Série 1 - corrigé
Rappels d’optique géométrique
20 février 2012
Exercice 1 – Tracé de rayons
Cas 1 : Optique de relais
γt =
€
A'B'
AB
=
€
f1
f2
Cas 2 : La loupe

2
€
γ
t=1
1+O
1A
O
1F
1'
=O
1F
1'
O
1A+O
1F
1'
Remarques :
1- Tel que représenté sur la figure
€
O
1A
est une quantité négative (la convention usuelle fixe
le sens positif comme allant de la gauche vers la droite). Plusieurs cas peuvent être
envisagés: Pour
€
O
1A<O
1F
1'=−O
1F
1
,
€
γ
t>1
, si maintenant on place l’objet AB en F1, alors
€
γ
t→+∞
et l’image virtuelle est à l’infini. Si finalement on place l’objet AB au delà de
F1, alors d’une part l’image intermédiaire deviendra réelle, le grandissement sera inversé
et il deviendra difficile, selon la longueur focale de la loupe, pour le cristallin de former
une image nette sur la rétine.
2- On remarque que l’usage de la loupe permet la création d’une image intermédiaire
agrandie de l’objet. Toutefois, la position de cette image est différente de celle de l’objet
étudié. Le grandissement transverse n’est alors plus une bonne mesure du pouvoir
« grossissant » de la loupe. De ce fait, il est généralement plus judicieux de qualifier ce
dernier en terme de grandissement angulaire qui, lui, est indépendant de la distance de
formation de l’image.

3
Cas 3 : Téléobjectif
L’intérêt principal d’un téléobjectif (association d’une lentille convergente et divergente comme
schématisée dans cet exercice) est d’obtenir un objectif photographique à très longue focale
(typiquement de 100 mm à 500 mm, mais pouvant aller jusqu’à plus de 1000 mm) sans devoir
placer la lentille objectif à 500 mm (ou 1 mètre !) du capteur pour autant, ce qui serait très peu
pratique et à la fois, très encombrant.
Exercice 2 – Points cardinaux
a) Soient les points Y1 et Y2 appartenant aux plans objet et image respectivement. De façon
générale on a
€
y2
n'
θ
2
#
$
%
&
'
( =A B
C D
#
$
%
&
'
(
y1
n
θ
1
#
$
%
&
'
(
. Les plans ici considérés étant conjugués, les points
Y1 et Y2 sont stigmatiques, i.e. tous les faisceaux émergeant de Y1 passent par Y2, d’où
T(A1A1’)=
€
A0
C D
"
#
$
%
&
'
b) Grandissement transverse γt=
€
y2/y1=A
Grandissement angulaire γa=
€
θ
2/
θ
1=n/n'×D

4
T(A1A1’)=
€
γ
t0
C
γ
a
#
$
%
&
'
(
c) Quand on multiplie T(A1A1’) par une matrice de déplacement d quelconque le long de
l’axe optique
€
1d/n
0 1
"
#
$
%
&
'
, le coefficient C reste inchangé, i.e est invariant. On peut donc
posé C=-V (Vergence)
T(A1A1’)=
€
γ
t0
−V
γ
a
$
%
&
'
(
)
d) En faisant le produit des trois matrices T(A2A1)=
€
1−d/n
0 1
#
$
%
&
'
(
, T(A1A1’) et T(A1’A2)=
€
1d' / n'
0 1
"
#
$
%
&
'
on obtient:
T(A2A2’)=
€
γ
t−Vd'
n'−
γ
t
d
n+
γ
a
$
d
n+Vd$
d
n$
n
−V
γ
a
$
n
n+Vd
n
%
&
'
'
'
(
)
*
*
*
Les plans repérés par A2 et A2’ sont conjugué si
€
−
γ
t
d
n+
γ
a
$
d
n+Vd$
d
n$
n
=0
On en déduit la relation de conjugaison
€
γ
a
d−
γ
t
$
d =−V
$
n =−1
$
f
On remarquera que les nouveaux grandissements transverse et angulaire sont
€
γ
t−Vd'
n'
et
€
γ
a
#
n
n+Vd
n
respectivement.
e) Soit xo et xi les positions objet et image définies par rapport à H et H’ respectivement.
Comme γt=1, on obtient
€
γ
a
xo
−1
xi
=−1
$
f
en utilisant la question précédente
La relation d’Abbe (condition d’aplanatisme) s’écrit
€
n⋅y1⋅
θ
1=n'⋅y2⋅
θ
2
. On en déduit la
relation importante
€
γ
t×n
n'
γ
a=1
d’où
€
n/"
n
xo
−1
xi
=−1
"
f
relation bien connue pour une lentille mince où H=H’
T(HH’)=
€
1 0
−V n' / n
#
$
%
&
'
(
f) Par définition F’ est l’image d’un point objet à l’infini xo
€
→ ∞
. A partir de la relation de
conjugaison on obtient xi=
€
"
H "
F ="
f

5
De même
€
HF =−n/#
n #
f =f
g) En utilisant de nouveau la relation de conjugaison on trouve
€
HN
=
€
"
H "
N =f+"
f
.
h) En utilisant la formule de passage pour les grandissements obtenus à la question d) on a:
€
A=
γ
t−Vd'
n'=1−V$
H S
n'
et
€
D=
γ
a
#
n
n+Vd
n=1+VHE
n
(entre les plans principaux
€
γ
t
=1
et
€
γ
a=n'
n
)
On en déduit
€
EH =f(D−1)
et
€
S"
H =f'(A−1)
Ces relations nous montrent que la connaissance de la matrice de transfert d’un
système optique entre E et S permet de déduire immédiatement H et H’.
Relations importantes:
€
EH =f(D−1)
€
S"
H =f'(A−1)
avec T(ES)=
€
A B
C D
"
#
$
%
&
'
€
"
H "
F ="
f
€
HF =−n/#
n #
f =f
Les points focaux sont repérés à partir des points principaux !
T(A1A1’)=
€
γ
t0
−V
γ
a
$
%
&
'
(
)
€
γ
t×n
n'
γ
a=1
€
V="
n
"
f
Important: Tout système optique se ramène à la connaissance de la position des points
cardinaux: points principaux (H et H’) et foyers (F et F’). La connaissance de H, H’, F et F’
permet la détermination de tous les rayons traversant le système.
(Remarque: à la place des points H, H’, F et F’ on peut évidement choisir comme autre
combinaison les points N, N’, F et F’ par exemple.)
 6
6
 7
7
1
/
7
100%