TD 1S7

Chapitre Correction des exercices
16
Exercice 3 page 284
a. Ec=1
2M·v2pour l’automobiliste en mouvement de translation.
b. Ec=1
2m·v2n’est pas applicable à la jante en mouvement de rotation mais est applicable lorsque qu’elle
est en mouvement de translation (freinage, roue bloquée).
Exercice 4 page 284
a. L’expression de l’énergie potentielle de pesanteur est Epp =Mgz si Epp(O) = 0 J. Si O est confondu avec
B, Epp(B) = 0 J. Donc Epp(A) = M gzA=M gdA
b. Si O est situé au plafond, zA=−d1et zB=−(d1+d2)donc Epp(A) = −M gd1et Epp(B) = −M g(d1+d2)
c. Si O est confondu avec B, Epp(B)=0J et Epp(A) = MgzA=M gd2donc la variation est :
Epp(B)−Epp(A) = 0 −Mgd2=−Mgd2
Si O est est situé au plafond, Epp(B) = −M g(d1+d2)et Epp(A) = −Mgd1donc la variation est :
Epp(B)−Epp(A) = −M g(d1+d2)−(−M gd1) = −M gd2
Ainsi, la variation d’énergie potentielle entre les points A et B ne dépend pas du choix de l’origine de Epp.
Exercice 9 page 285
L’énergie cinétique d’un objet en translation est Ec=1
2m·v2.
a. La masse de l’avion est m= 180 t = 1,8×105kg et sa vitesse v= 860 km ·h−1=860 ×103
3600 m·s−1.
Ec= 5,14 ×109J
b. La masse de l’escargotest m= 12 g = 1,2×10−2kg et sa vitesse v= 5,0 m ·h−1=5,0
3600 m·s−1.
Ec= 1,2×10−8J
c. Le vase est immobile par rapport à la Terre, sa vitesse dans le référentiel terrestre est nulle, donc son
énergie cinétique est nulle.
Exercice 10 page 285
a. Epp =mgz = 1,8×105×9,8×10 ×103= 1,8×1010 J
b. Epp = 0 J.
a. Epp =mgh = 600 ×10−3×9,8×85 ×10−2= 5,0J

Lycée Camille Vernet Thème : Lois et modèles 2/6
Exercice 13 page 287
Dans le référentiel terrestre, on étudie la balle en interaction avec la Terre. Epp est choisie nulle à l’altitude
du sol.
a. Ec(t0) = 1
2m·v2
0=1
2×58,0×10−3×116 3,62
= 30,1J.
Epp(t0) = mgh = 58,0×10−3×9,8×2,40 = 1,4J.
b. Epp(t1) = 0 J.
Sans apports d’énergie et si on ne tient pas compte des forces de frottements, l’énergie mécanique du système
se conserve :
Em=cte =d’où Em(t0) = Em(t1)
Soit Epp(t0) + Ec(t0) = Epp(t1) + Ec(t1)
Ainsi Ec(t1) = Epp(t0) + Ec(t0)−Epp(t1) = 30,1+1,4−0 = 31,5J.
c. Ec(t1) = 1
2m·v2
1d’où v1=r2Ec(t1)
m=r2×31,5 58,0×10−3= 33,0m·s−1
d. En tenant compte des frottements de l’air, l’énergie mécanique ne se conserve pas mais décroît sans cesse.
Il y a dissipation d’énergie par transfert thermique :
Ec(t1)<31,5J et v < 33,0m·s−1
Exercice 14 page 287
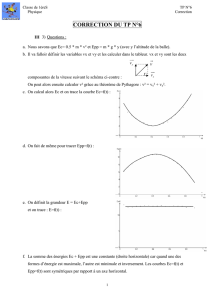
a. La courbe 1 correspond donc aux variations de l’énergie cinétique.
L’altitude de la plongeuse augmente puis diminue. Epp(t) = mgz(t)subit les mêmes variations. La courbe 3
traduit les variations de l’énergie potentielle de pesanteur.
La courbe 2 correspond donc à Em, ce qui traduit le fait que l’énergie mécanique se conserve du fait d’absence
de frottements et d’apport d’énergie au cours du plongeon.
b.
c. h0= 3,2m et hmax = 3,9m
d. v2=√2gh1=√2×9,8×3,9=8,7m·s−1(31 km ·h−1).

Lycée Camille Vernet Thème : Lois et modèles 3/6
Exercice 15 page 287
a. Une fois la bille lancée, l’énergie mécanique du système se conserve du fait de l’absence de frottement et
d’apport d’énergie.
b. ∆`=`final −`initial. Comme le ressort est comprimé, `final < `initial et ∆` < 0
c. Entre Aet O, la variation d’énergie du système {bille en interaction avec la Terre }est nulle car la balle
ne change pas d’altitude et sa vitesse est nulle en Aet O.∆Em=OJ
Remarque : si on inclut le ressort et le support dans le système, la variation d’énergie n’est pas nulle puisque
le ressort peut stocker l’énergie reçue de la part du joueur de flipper qui agit sur la tirette.
∆E0=Em(A)−Em(O) = Ec(A) + Epp(A) + Epe(A)−Ec(O)−Epp(O)−Epe(O)
or Epp(A) = Epp(O)car Aet Osont à la même altitude. Epe(O)=0J compte tenu du choix de l’origine de
l’énergie potentielle élastique et Ec(A) = Ec(O)=0J du fait que les vitesses de la bille sont nulles en Aet O.
Ainsi ∆E0=1
2K(∆`)2=1 2·50 ·(−10 ×10−2)2= 2,5×10−1J .
d. Pour appliquer le principe de conservation de l’énergie mécanique, le système ne doit pas recevoir d’énergie
ni en dissiper. Si on inclut le ressort dans le système, une fois la tirette lâchée, il n’y a pas d’apport d’énergie
au système et donc, en l’absence de frottement, l’énergie mécanique se conserve :
Em=cte =d’où Em(0) = Em(A)
soit Ec(O) + Epp(O) + Epe(O) = Ec(A) + Epp(A) + Epe(A)
or Epp(A) = Epp(O)car Aet Osont à la même altitude. Epe(O)=0J compte tenu du choix de l’origine de
l’énergie potentielle élastique et Ec(A)=0J car la vitesse de la bille en Aest nulle.
Ainsi Ec(O) = Epe(A)
Soit 1
2mv2
O=1
2K(∆`)2d’où vO=rK m(∆`) = r50 80 ×10−3×10 ×10−2= 2,5 m ·s−1
Remarque
On peut aussi garder comme système la bille en interaction avec la Terre. Dans ce cas, on peut écrire que la
variation d’énergie mécanique est égale à l’énergie transférée au système par le ressort :
Em(0) −Em(A) = 1
2K(∆`)2
Ec(O) + Epp(O)−Ec(A)−Epp(A) = 1
2K(∆`)2
or Epp(A) = Epp(O)car Aet Osont à la même altitude et Ec(A)=0J car la vitesse de la bille en Aest nulle.
d’où 1
2mv2
O=1
2K(∆`)2d’où vO=rK m(∆`) = r50 80 ×10−3×10 ×10−2= 2,5 m ·s−1

Lycée Camille Vernet Thème : Lois et modèles 4/6
Exercice 17 page 288
a.
b. Dans le référentiel terrestre, on étudie le pendule en interaction avec la Terre. Sans apports d’énergie et
si on ne tient pas compte des forces de frottements, l’énergie mécanique se conserve.
Em=cte d’où Em(O) = Em(D)
soit Ec(O) + Epp(O) = Ec(D) + Epp(D)
On choisit :
— l’énergie potentielle de pesanteur nulle à l’altitude de O;
— un axe (Oz) vertical orienté vers le haut.
Alors Epp(D) = mgzDavec zD= +h1.
En outre, la vitesse en Dest nulle.
La relation s’écrit donc : 1
2m·v2
O+ 0 = 0 + mgh1soit vO=√2gh1
A.N. : vO=√2×9,8×3,2=7,9m·s−1(≈28 km ·h−1).
c. Si Tarzan ne lâche pas la corde, un raisonnement identique permet de montrer que Tarzan remonte à une
altitude h= 3,2 m en l’absence de frottement ou d’apport d’énergie.
d. Tarzan quitte Davec une vitesse vDet atteint Fsitué h2= 4,0m au-dessus de O. Le calcul de la valeur
minimale de la vitesse en Dpour atteindre Fsuppose l’absence de frottement.
Ainsi : Em=cte d’où Em(F) = Em(D)
soit : Ec(F) + Epp(F) = Ec(D) + Epp(D)
et : 0 + mgh2=1
2m·v2
D) + mgh1
A.N. : vD=p2g(h2−h1)p2×9,8×(4,0−3,2) = 4,0m·s−1

Lycée Camille Vernet Thème : Lois et modèles 5/6
Exercice 23 page 289
aÀt0= 0 s, la vitesse du solide est nulle Ec(t0)=0J, la courbe verte correspond à Ec.
En début d’étude, la balle chute vers le bas puis rebondit : son altitude décroît puis croît Epp diminue puis
augmente, la courbe bleue traduit les variations de Epp.
b. La balle touche la table à t1=0,45 s, ce qui correspond graphiquement à Epp(t1)=0J.
c. En dehors du choc, si on suppose que la balle est en chute libre, l’énergie cinétique et l’énergie potentielle
s’échangent l’une et l’autre de telle sorte que l’énergie mécanique Emsoit conservée :Em=Ec+Epp =cte.
Ainsi, pour t06t6t1:Em=Ec(t0) + Epp(t0) = 0 + 0,98 = 0,98 J ;
pour t1< t 6t2:Em=Ec(t2) + Epp(t2) = 0 + 0,70 = 0,70 J.
Construction du graphique des variations de l’Emen fonction du temps.
- Tracer deux segments de droite horizontaux ayant pour extrémités les points :
•d’abscisses 0 s et 0,45 s, et pour ordonnée commune 0,98 J ;
•d’abscisses 0,47 s et 0,90 s, et pour ordonnée commune 0,70 J.
- Tracer un segment de droite décroissante qui relie les deux segments précédents.
d. Pendant le choc, la balle se comprime puis se dilate. Il y a échange entre énergie cinétique et énergie dite
potentielle élastique (cette énergie est constante avant et après le choc puisque, en dehors du choc, la balle ne
se déforme pas. On la choisit nulle). D’autre part, une partie de l’énergie mécanique du système est transférée
vers le milieu extérieur, notamment la table, ce qui entraîne une diminution de l’énergie mécanique.
e. L’énergie potentielle maximale acquise par la balle après le rebond est Epp(t2)=0,70 J. En considérant
que Epp = 0 J, pour une altitude z= 0 m, on peut écrire Epp(t2) = mgz(t2). Ainsi, l’altitude maximale
atteinte par la balle après le rebond est :
z(t2) = Epp(t2)
mg =0,70 0,100 ×9,8= 0,71 m = 71 cm