Partiel - Physique 4 - e

Partiel - Physique 4
CPI
Le candidat attachera la plus grande importance à la clarté, à la précision et à la concision
de la rédaction. Si un candidat est amené à repérer ce qui peut lui sembler être une erreur
d’énoncé, il le signalera sur sa copie et devra poursuivre sa composition en expliquant les
raisons des initiatives qu’il a été amené à prendre.
Durée : 1 Heure 20 min
Enseignant : J.Geandrot
Exercice 1 : QCM (3pts)
Une seule réponse par question doit être cochée. Une bonne réponse entraîne un gain
de 0,5 point et toute mauvaise réponse entraîne une perte de 0,2 point. Il ne faut donc pas
répondre au hasard.
1.1 On cherche le champ créé par une distribution de charge en un point M. Le système de
coordonnée choisi est le système cylindrique. On peut trouver un plan d’antisymétrie de
la distribution passant par M et défini par (
−→
ur,−→ uz
); on repère également une invariance
par translation suivant −→ ur.
Quelle est l’expression générale simplifiée du champ électrique créé par cette distribution
en M ?
−→ E=E(r,z)−→ ur+E(r,z)−→ uz
−→ E=E(r,θ)−→ ur
√−→
E=E(θ,z)−→ uθ
−→ E=E(θ,z)−→ uθ+E(r,z)−→ uz
−→ E=E(r,z)−→ uθ
−→ E=E(r,θ)−→ ur+E(r,θ)−→ uθ
1.2 Quelle est l’expression qui traduit correctement l’énoncé du théorème de Gauss ?
¨S
−→
E∧−−→ next dS=Qint 0
˛L EdS=Qint 0
√‹S
−→
E·−−→ next dS=Qint
0
‹S Q next dS=Eint
0
¨S
−→
E·−−→ next dS=0
Qint
1.3 On donne les expressions usuelles :
– d’une puissance mécanique P =
−→
F·−→ v ;
– d’une puissance électrique P=U×I;
– de l’intensité d’un courant I=dq
dt;
– d’une force électrostatique
−→
F = q−→ E .

Retrouver l’unité d’un champ électrique.
V.s
V.m
√V.m−1
A.s−1
V.s−1
1.4 L’expérience du Danois Oersted en 1820 montre :
qu’un morceau d’ambre frotté attire des petits objets ;
que si on fait varier le flux d’un champ magnétique à travers un circuit
électrique on créé un courant électrique ;
que des corps isolants peuvent se polariser sous l’effet d’un champ électrique ;
√qu’un fil parcouru par un courant créé un champ magnétique per-
pendiculaire au fil.
1.5 Choisir la bonne proposition :
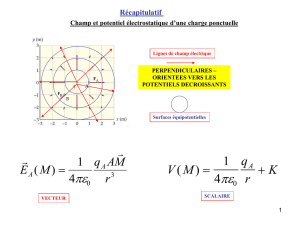
Lignes de champ et lignes équipotentielles sont toutes les deux orientées et
perpendiculaires les unes aux autres ;
Selon la distribution de charges étudiés, lignes de champ et équipotentielles
peuvent être confondues.
Les lignes de champs sont en tout point perpendiculaires aux volumes équi-
potentielles.
√Les lignes de champ sont orthogonales aux surfaces équipotentielles
pour n’importe quelle distribution chargée ;
Les surfaces équipotentielles sont orientées en sens inverse des lignes de champ
mais tangentes à celles-ci en tout point.
1.6 Que devient le dipôle dans la configuration ci-contre :
−→
E
−→
E−→ E
•
(+q)
P•
(-q)
N
−→
p
Il ne se déplace pas mais pivote dans le sens des aiguilles d’une montre pour
se positionner horizontalement ;
Il se déplace vers la gauche en gardant la même orientation ;
√Il pivote pour se positionner horizontalement, −→
pétant dirigé vers
la gauche et se déplace vers la droite ;
Il s’oriente dans le sens inverse du champ −→ Eet se déplace vers le haut ;
Il ne se déplace pas mais pivote dans le sens inverse des aiguilles d’une montre
pour se positionner verticalement ;
Il prend une position horizontalement symétrique à celle qu’il a et se déplace
vers la droite.
Partiel Physique 4 Page 2/4

Exercice 2 : questions de cours (8,5pts)
2.1. Représenter sur un schéma, pour chaque cas, les lignes de champ et équipotentielles :
◦d’une charge électrique négative ;
◦d’un dipôle électrostatique ;
◦d’un condensateur plan, dans l’espace inter-armatures.
2.2. Soit une charge q1 qui subit un potentiel électrostatique V2 créé par une charge q2 .
L’énergie potentielle de la charge q1 vaut EP1 = q1V2 (l’origine des énergies potentielles
est prise à l’infini).
Etablir l’expression de l’énergie potentielle de l’ensemble de charges suivant, en fonction
de q,aet 0:
+q+q
−2q
a a
a
2.3. Déterminer le potentiel électrostatique correspondant au champ électrique suivant :
−→
E=2kcos θ
r3−→
ur+ksin θ
r3−→
uθ
où kest une constante. On prendra l’origine des potentiels à l’infini.
2.4. Déterminer le champ électrostatique correspondant au potentiel suivant :
V=λ R
20
1
√R2+z2
où λet Rsont des constantes. L’origine des potentiels est prise à l’infini.
Exercice 3 : champ électrique créé par une demi-sphère chargée en
surface (8,5pts)
Soit une demi-sphère de centre O, de rayon R , chargée uniformément en surface avec la
densité surfacique de charge σconstante et positive.
On cherche à établir l’expression du champ électrostatique créé par cette demi-sphère au
point O , centre de celle-ci et origine du repère cartésien. On utilise la méthode intégrale.
Partiel Physique 4 Page 3/4

Ci-dessous est représenté en coupe la demi-sphère chargée (en gras) ainsi qu’un rappel de la
définition des coordonnées sphériques.
Oy
z
x
(σ)
Vue de côté
−→
ux
−→
uy
−→
uz
−→
ur
−→
uθ
−→
uϕ
−→
uϕ
•
P(r,θ,ϕ)
r
ϕ
θ
3.1. Quel système de coordonnées faut-il choisir pour traiter ce problème : cartésien, cylin-
drique, polaire, ou sphérique ?
3.2. Dans le système de coordonnées choisi, donner l’expression générale du champ électrique
(coordonnées de dépendance et composantes).
3.3. Etudier en justifiant les invariances de ce problème, en déduire une expression simplifiée
du champ électrique donné précédemment. On rappelle que l’on cherche le champ
électrique en O.
3.4. Etudier en justifiant les symétries et/ou antisymétries du problème, en déduire une
nouvelle expression simplifiée du champ électrique en O.
3.5. On considère un point P de la demi-sphère chargée sur lequel est centré un élément
infinitésimal de surface dS.
3.5.1. Représenter sur le schéma de la semi-sphère ci-dessus le point P, ses coordonnées
et le champ d−→ Ecréé en O par l’élément dScentré sur P.
3.5.2. Quelle est l’expression de ce champ d
−→
E ? La donner en fonction de σ ,d S , 0 , P O
et −→ P O.
3.6. Une projection du champ élémentaire donné précédemment permet de simplifier l’inté-
gration qui va suivre.
Effectuer celle-ci.
3.7. Sachant que l’élément infinitésimal de surface en coordonnées sphériques a pour expres-
sion d S = R2sin θ d θ d ϕ , calculer le champ électrique en O créé par la demi-sphère
chargée.
Indications
◦ dans tout cet exercice, ne pas confondre r la coordonnée et R le rayon de la demi-sphère
chargée ;
Partiel Physique 4 Page 4/4

◦ dans la dernière question, il s’agit de trouver les bornes d’intégration qui permettent de
parcourir toute la surface de la demi-sphère chargée.
CORRECTION
Exercice 2
2.1. Lignes de champ et équipotentielles :
•Charge négative :
-q
•Dipôle électrostatique :
−→
p
Lignes de champ
Equipotentielles
•Condensateur plan
Partiel Physique 4 Page 5/4