1 Exercice : polarisation d`une superposition d`ondes planes.

Phys325 Ondes électromagnétiques et optique Année 2004-2005
Partiel (durée 1h30 minutes)
Documents autorisés : Les seuls documents autorisés sont le formulaire et une feuille ”Antisèche”
A4 recto verso ou figure toutes les informations souhaitées.
La calculatrice est autorisée.
1 Exercice : polarisation d’une superposition d’ondes planes.
On considère deux ondes électromagnétiques planes progressives monochromatiques de longueur
d’onde λde même amplitude E0. La première ( ~ E1) est polarisée selon 0yelle se propage selon l’axe
0xvers les xcroissants. La seconde ( ~ E2) est polarisée selon 0xelle se propage selon l’axe 0yvers
les ycroissants. Les deux ondes sont en phase à l’origine (et l’on choisira cette phase nulle).
On se placera pour tout l’exercice dans le plan x0y.
1. Ecrire l’amplitude de ces deux ondes.
2. Que vaut le champ électrique à l’origine ? Quelle est sa polarisation en ce point
3. Que vaut le champ électrique au point ( x=λ
4,y= 0) ? Quelle est la polarisation en ce point ?
4. Que vaut le champ électrique au point ( x=3λ
4,y=λ 4) ? Quelle est la polarisation en ce point ?
5. Déterminer l’ensemble des points pour lesquels la polarisation est linéaire.
Université Pierre et Marie Curie

Phys325 Ondes électromagnétiques et optique Année 2004-2005
2 Problème : antenne dièdre
2.1 Préliminaire : Réseau de sources isotropes
On considère un réseau plan formé de quatre sources isotropes disposées chacune sur l’un des axes
à une distance dde l’origine comme l’indique la figure 1. Les sources 1 et 4 sont en phase, les sources
2 et 3 sont en opposition de phase par rapport aux précédentes. Toutes sont alimentées avec la même
puissance et émettent un rayonnement de longueur d’onde λ. L’origine des phases est celle d’une
source qui serait placée à l’origine des coordonées, en phase avec la source 1. Soit E0l’amplitude du
champ créé par une seule source à grande distance, en un point Mde coordonnées (R, θ, ϕ).
Fig. 1: réseau composé de 4 sources isotropes
On se placera pour tout l’exercice dans le plan x0y.
2.1.1 Analyse qualitative du problème
Ces questions ont pour objectif de déterminer des propriétés du diagramme de rayonnement dans
certaines directions particulières. Résolues correctement elles seront un guide qui permettra de vérifier
la pertinence des résultats obtenus par le calcul. Elle seront une aide utile pour le tracé du diagramme
de rayonnement.
Pour chacune de ces questions, on fera un schéma descriptif.
1. Montrer que sur les bisectrices des axes (ie : la droite définies par x=yet la droite définie par
x=−y) le champ électrique est nul, quelque soit la distance à l’origine et la distance entre les
sources.
2. On considère un point situé sur l’axe 0x,
a) Montrere que les champs reçus des sources 2et 3est toujours en phase.
b) A quelle condition les champ reçus des sources 1et 4sont ils en phase ?
c) Montrer que quand la condition best vérifiée, si l’on se trouve à grande distance de la
source (Rd),les quatre champs sont en phase.
Université Pierre et Marie Curie

Phys325 Ondes électromagnétiques et optique Année 2004-2005
2.1.2 Calcul du diagramme de rayonnement
1. Donner l’expression exacte du champ électrique total Etsomme des champs électriques E1,E2,
E3et E4émis par chacune des sources. On pourra utiliser dans cette expression les distances r1
,r2,r3et r4qui séparent le point Mde chacune des sources.
2. Donner une expression approchée des distances r1,r2,r3et r4lorsque le point Mse trouve
à grande distance de l’orgine (Rd)
3. En déduire une expression simplifiée à grande distance du champ total Etcréé par les quatre
sources en fonction de E0et de Ret ϕ. Et vérifier que le résultat obtenu vérifie les propriétés
déterminées lors de l’analyse qualitative.
4. Que vaut le diagramme de rayonnement en champ F(ϕ) = |Et|
|Et|max
dans ce plan, dans le cas
où les sources sont distantes de l’origine d’une demi longueur d’onde d=λ/2.
5. Tracer La forme approximative de ce diagramme (on s’aidera de la partie qualitative).
Application à l’antenne dièdre
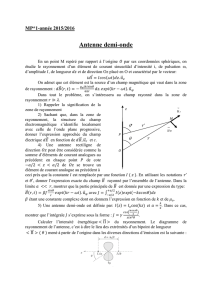
Une antenne dièdre, représentée sur la figure 2, est formée d’un dipôle (doublet) de longueur λ/2
placé entre deux demi-plans réflecteurs formant un angle droit. L’axe du doublet est parallèle à l’arête
du dièdre qui définit l’axe 0z, il est distant de d. Les réflecteurs sont supposés être des conducteurs
parfaits.
Fig. 2: antenne dièdre
Université Pierre et Marie Curie

Phys325 Ondes électromagnétiques et optique Année 2004-2005
Soit E0(R, θ, ϕ)le champ créé en un point de l’espace par le doublet en l’absence des plans réflecteurs
et f(θ, ϕ)le diagramme en champ correspondant.
Il est donné par la relation : f(θ, ϕ) = 
cos π
2cosθ
sinθ
Soit E1(R, θ, ϕ)le champ rayonné au même point par l’antenne dièdre.
On peut montrer (par la méthode des images électriques) que le système de l’antenne diedre est
équavalente au problème précédent : dans le quadrant eclairé par l’antenne, tout se passe comme si
l’emetteur etait un ensemble composé de 4 éléments (ici dipôles demi-onde) : 2 en phase (1 et 4) et
2 en opposition de phase (2 et 3).
1. Exprimer le champ E1en fonction de E0,ϕ,det λ, pour un point situé à grande distance dans
le plan x0y.
2. Étudier la forme du diagramme dans le plan x0y, pour d=λ/2.
3. Quel peut être l’intérêt d’une telle antenne ?
Diagrammes de rayonnement d’une antenne dièdre
dans les plan E (élévation) et H (azimuth)
Université Pierre et Marie Curie