chapitre sur les triangles

Les triangles
1 Définitions et triangles particuliers
Définition 1 Un triangle c’est un polygone qui a trois côtés.
Exemples 1 Dessiner trois triangles, un classique, un qui est équilatéral, et un
qui a un angle obtus.
Définition 2 Un triangle rectangle c’est un triangle qui a un angle droit.
Si un triangle ABC a son angle droit au sommet A, on dit que ABC est rec-
tangle en A. De plus le côté qui est en face de l’angle droit s’appelle l’hypo-
ténuse.
L’hypoténuse ça servira beaucoup l’an prochain
Exemples 2 Faire trois dessins, un avec le triangle rectangle posé sur un côté
de l’angle droit, un posé sur l’hypoténuse, et un dans une figure complexe, avec
une justification.
Définition 3 Un triangle isocèle c’est un triangle qui a (au moins) deux côtés
égaux. Le sommet qui touche les deux côtés égaux s’appelle le sommet principal
et le côté qui est opposé au sommet principal s’appelle la base du triangle isocèle.
Exemples 3 Faire deux dessins, un posé sur la base et un posé sur l’un des deux
côtés égaux. Indiquer le vocabulaire : base et sommet principal. Et en marquant
les côtés égaux.
Définition 4 Un triangle équilatéral c’est un triangle qui a trois côtés égaux.
Exemples 4 Faire deux dessins, un petit et un plus grand en marquant les côtés
égaux.
1

Remarque 1 Un triangle équilatéral est un triangle isocèle.
Dans un triangle isocèle, les deux angles qui touchent la base sont égaux.
2 Tracé d’un triangle dont on connaît les trois
côtés
On veut tracer un triangle dont on connaît les trois côtés.
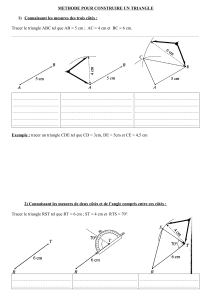
. Par exemple tracer le triangle ABC tel que AB = 7 cm, BC = 10 cm et CA =
6 cm.
Méthode
Préalable Faire un dessin à main levée pour se
faire une idée et se rappeler de la mé-
thode.
Etape 1 On trace un (le plus grand) côté. Faire le dessin du segment
[AB]
Etape 2 On trace un arc de cerle de longueur 6
cm en pointant le compas en A.
Faire le dessin du segment
[AB] et de l’arc de cercle
Etape 3 On trace un arc de cercle de longueur
10 cm en pointant le compas en B.
Faire le dessin du segment
[AB] et des deux arcs de
cercle.
Etape 4 On place le point C à l’intersection des
deux arcs de cercle, et tracer [BC] et
[CA].
Faire le dessin du triangle
complet.
Exemples 5 Tracer les triangles suivants :
1. ABC tel que AB = 4 cm, BC=5 cm, et CA = 3 cm
2. IJK tel que IJ= 3 cm, JK=7 cm et KI=7 cm
3. ZUT tel que ZU=5 cm, UT=5 cm et TZ=5 cm
4. GIL tel que GI = 10 cm, IL = 4 cm et LG = 5 cm
2

3 Inégalité triangulaire
On a remarqué que l’on ne pouvait pas tracer certains triangles.
Théorème 1 Dans un triangle la somme des longueurs des deux petits côtés
est toujours supérieure à la longueur du grand côté.
C’est même mieux, dans un triangle la somme des longueurs de deux côtés est
toujours supérieure à la longueur du troisième côté.
Autrement dit :
Dans un triangle ABC : AB<AC+BC
Exemples 6 Tracer les trois triangles suivants après avoir anticipé si ils exis-
taient.
1. EFG tel que EF = 7 cm, FG = 5 cm et GE = 6 cm
2. IJK tel que IJ = 10 cm, JK = 6 cm et KI = 3 cm
3. TUV tel que TU = 12 cm, UV = 6 cm et VT= 6 cm
Remarque : Et si la somme des deux petits côtés est égale au troisième côté.
Théorème 2 Dans un triangle ABC, si la somme des longueurs des deux petits
côtés d’un triangle est égale à la longueur du troisième côté, alors les points A ;
B et C sont alignés.
4 Tracer d’un triangle dont on connaît un côté et
les angles
On veut tracer un triangle ABC tel que AB = 10 cm, ˆ A= 30˚et ˆ B= 60˚.
Méthode
Préalable Tracer un dessin à main levée pour se
faire une idée
Etape 1 Tracer le côté que l’on connaît, ici [AB] Tracer [AB]
Etape 2 Tracer l’angle ˆ Ade 30˚en prenant [AB]
comme l’un des côtés
Tracer [AB] et l’angle ˆ A
Etape 3 Tracer l’angle ˆ Bde 60˚en prenant [AB]
comme l’un des côtés
Tracer [AB] et les deux
angles.
Etape 4 Placer le point C à l’intersection des
deux côtés que l’on vient de tracer. Et
tracer le triangle ABC
Dessiner ABC
3

Tracer les triangles suivants.
1. ABC tel que AB=7 cm, ˆ A=45˚et ˆ B= 45˚
2. EFG tel que EF = 5 cm, ˆ E=40˚et ˆ F=40˚
3. KIL tel que KI = 7 cm, ˆ K=40˚et ˆ I=50˚
5 Tracer un triangle dont on connaît deux côtés
et un angle
On veut tracer un triangle ABC tel que AB = 10 cm, BC=8 cm et ˆ B= 60˚.
Méthode
Préalable Tracer un dessin à main levée pour se
faire une idée
Etape 1 Tracer un des côtés que l’on connaît, ici
[AB]
Tracer [AB]
Etape 2 Tracer l’angle ˆ Bde 60˚en prenant [AB]
comme l’un des côtés
Tracer [AB] l’angle ˆ B
Etape 3 Tracer le point C sur le deuxième côté
de l’angle ˆ Bà la distance donnée dans
l’énoncé
Tracer ˆ Bet les deux
points A et C sur ses cô-
tés.
Etape 4 Tracer le côté qui manque [AC] Dessiner ABC
Tracer les triangles suivants.
1. ABC tel que AB=7 cm, BC=5cm et ˆ B= 45˚
2. EFG tel que EF = 5 cm, FG = 6 cm et ˆ F=40˚
3. KIL tel que KI = 7 cm, IL = 7 cm et ˆ I=50˚
4

6 Médiatrice, définition et propriétés
Définition 5 La médiatrice d’un segment [AB] c’est la droite qui est perpen-
diculaire à [AB] et qui passe par son milieu.
Exemples 7
AB
90˚
D
E
90˚
Théorème 3 Si un point est sur la médiatrice d’un segment, alors il est à la
même distance des extrémités de ce segment.
Et réciproquement, si un point est à égale distance des extrémités d’un seg-
ment, alors il est sur la médiatrice.
Exemples 8
5