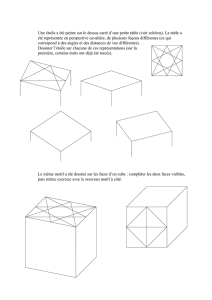
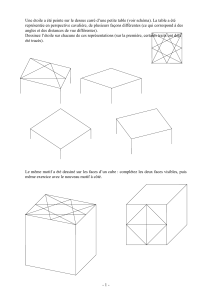
STRUCTURER L`ESPACE PAR L`ETUDE DES POLYEDRES

STRUCTURER L'ESPACE
PAR L'ETUDE DES
POLYEDRES REGULIERS
III ISOMETRIES DU CUBE EN 1°S ET TS
ESSAI PEDAGOGIQUE

1
J-P Daubelcour
IREM DE LILLE
3° PARTIE ISOMETRIES DU CUBE
en 1°S et TS
ESSAI PEDAGOGIQUE
Chapitre I Généralités sur les figures isométriques de l'espace.
Chapitre II Isométries du cube et propriétés des isométries de l'espace
Chapitre III Synthèse sur les isométries de l'espace.
Liminaire
L'objectif est une étude des isométries de l'espace par l'étude des isométries qui agissent sur
une figure : en l'occurrence le cube.
Dans un cadre plus général, il s'agit de réintroduire les figures comme "objet d'étude " de la
géométrie élémentaire au Lycée.
Nous pensons que l'étude des polyèdres, notamment des polyèdres réguliers est une des
façons les plus simples de structurer fortement l'espace : un bon point de départ pour un
enseignement qui veut aller des structures fortes aux faibles, du particulier au général, du
concret à l'abstrait. On commencera par démontrer qu'il n'existe que cinq polyèdres réguliers.
1° PARTIE En premier lieu les lois d'incidences dans l'espace sont découvertes en étudiant
la section d'un cube et d'un tétraèdre régulier par un plan sécant. Puis les définitions et
propriétés concernées sont formalisées.
2° PARTIE En second lieu l'orthogonalité des droites et des plans peut se découvrir en
étudiant le cube et tétraèdre régulier. Le cube donne des situations d'orthogonalité
immédiates, puis le tétraèdre régulier révèle des orthogonalités moins évidentes et qui
nécessitent l'acquisition d'une méthode. L'observation est suivie de la formalisation du
concept d'orthogonalité dans l'espace. Le produit scalaire dans l'espace est défini à cette
occasion.
3° PARTIE Les propriétés des isométries de l'espace sont étudiées à l'occasion de la
recherche des isométries qui conservent le cube. Il ne s'agit pas en terminale S d'une étude
exhaustive allant jusqu'à la classification de toutes les isométries de l'espace ; notamment il ne
sera question ni de déplacement hélicoïdal ni de translation-réflexion. La méthode
d'exposition de ce cours utilise un rythme ternaire : "stade iconographique, celui du dessin et
de la construction", "stade manipulatoire ou calculatoire ", enfin " le stade formel ou la
démonstration"; étapes classiques de la pédagogie de Jérôme Bruner1. Cette méthode permet
l'alternance d'une démarche empirique avec le développement formel des propriétés générales
des isométries de l'espace, au fur et à mesure de leur nécessité pour retrouver les 48 isométries
du cube.
Quant au difficile problème qui consiste à se libérer du "mouvement par superposition" pour
établir un critère d'égalité de deux figures de l'espace, l'originalité de ce travail consiste à
1 J. Bruner fut enseignant à Harvard en 1960. Sa démarche pédagogique, parfois présente dès l'école maternelle, a été
introduite au Lycée en France dans les années 70-80 à une époque où le rôle des calculatrices programmables
cherchait à se définir dans un processus rationnel d'enseignement de l'analyse au Lycée. Le stade "manipulatoire"
est alors celui du calcul.

2
transporter un repère orthonormé
ℜ
(
,
,
,
)
O
I
J
K
de l'espace et un point M(x,y,z) lié à ce repère
sur un repère orthonormé
ℜ
'( ', ', ', ')O I J K en remarquant que l'homologue M' de M dans ce
transport a également pour coordonnées (x, y,z) dans le repère.
Cette méthode présente en particulier l'avantage de faire le lien avec l'algèbre linéaire,
après le baccalauréat. En effet on peut constater qu'il est aisé de faire correspondre à
chaque isométrie du cube sa matrice dans une base orthonormée liée au cube.
Les prérequis : Calcul vectoriel et notion de barycentre et d'isobarycentre.
Dans la 1° et la seconde partie de ce cours de géométrie dans l'espace certaines questions ont
déjà été étudiées. Notons les relations d'incidence droites et plans de l'espace, le parallélisme
dans l'espace, l'orthogonalité et le produit scalaire dans l'espace, droites orthogonales, droite
orthogonale à un plan et plans perpendiculaires. Notons également les problèmes
d'équidistance avec : plan médiateur d'un segment, axe d'un carré ou d'un triangle équilatéral,
repères orthonormés de l'espace. Enfin la notion de transformations de l'espace a été
rencontrée à l'occasion des translations de l'espace, de la symétrie par rapport à un plan P
dite ici " réflexion de miroir P", de la symétrie-point dans l'espace. Enfin la composition des
transformations de l'espace et les groupes de transformations sont évoquées à propos du
groupes des translations et des , groupe des homothéties- translations de l'espace.

3
CHAPITRE I GENERALITES SUR LES FIGURES
ISOMETRIQUES DE L'ESPACE
I Axiomes définissant la relation d'égalité entre deux figures invariables de l'espace.
(Axiomes d'égalité par coïncidence).
• Par expérience, les corps solides ou indéformables se distinguent des corps fluides ou
déformables. Un objet métallique maintenue à température constante et non soumis à des
forces de déformation est un corps solide. Donc un corps solide est constitué de points tels
que la distance entre deux points donnés A et B existe est demeure constante. Si l'on
idéalise un corps solide, on obtient une figure invariable : ainsi un fil métallique idéalisé
est l'image d'une ligne ; une tôle métallique mince idéalisée est une l'image d'une surface ;
une règle métallique idéalisée est l'image d'un parallélépipède rectangle.
• Plus généralement soit une figure invariable S qui idéalise une salle de classe(un corps
solide)et la figure invariable F qui idéalise une règle métallique R tenue à un endroit
précis de cette salle par un élève. Soumis par l'élève à un mouvement quelconque, ce
solide R peut occuper plusieurs positions distinctes R', R"… par rapport à la salle S, plus
précisément par rapport à un repère orthonormé
ℜ
lié à S. Lorque ce solide R a quitté la
position initiale pour R', on sait dire où il se trouvait avant par rapport au repère
ℜ
, et où
ce trouvait un point précis de R : ainsi explique-t-on la notion de point M lié à un corps
solide, puis par abstraction la notion de point M lié à la figure invariable F. Par la
définition des figures, nous entrons ainsi dans le domaine de la géométrie de l'espace.
• A deux positions R' et R", lors du mouvement dans l'espace, de la règle R sont ainsi
associées deux figures invariables F' et F" : chaque point précis M' lié à F' peut venir en
coïncidence par ce mouvement avec un point précis M'' de F" : on dira que ces deux
figures "géométrique" invariables sont égales. Si la coïncidence point par point des
deux solides est irréalisable matériellement, nous convenons qu'elle soit possible pour les
figures géométriques idéales dont ces solides sont les images
• De même, considérons deux objets solides issus du même moule, ils sont images de deux
figures invariables ; de même que nous disons que les objets sont égaux, nous dirons que
les deux figures invariables ou "figures géométriques" associées sont égales.
Donc deux figures géométriques F' et F" sont égales si elles ont pour images deux positions
d'un même corps solide ou de deux corps solides issus du même moule.
• Désormais E désigne l'ensemble des points de l'espace idéalisation de l'espace
physique. Considérons les figures géométriques de l'espace dites simplement figures. La
relation d'égalité par superposition entre deux figures de l'espace est définie ainsi:
Définition 1 La figure F' de l'espace E est égale à la figure F" si on peut amener par un
mouvement dans l'espace F' en coïncidence point par point avec F".
Si F'est égale à F", tout point M' de F' peut venir en coïncidence avec un point M" de F" :le
point M" est l'homologue du point M'. Evidemment une partie donnée de F' vient en
coïncidence avec la partie "homologue" de F".
Propriété 1. La relation "égale par superposition" entre les figures géométriques est
réflexive, symétrique et transitive : c'est donc une relation d'équivalence.
La démonstration est aisée. En particulier la symétrie implique : si F' est une figure égale à F"
alors F" est égale à F : on peut donc dire que les figures F' et F"sont égales
Citons les autres axiomes les plus usuels : deux segments de même longueur sont des
figures égales.. Deux droites de l'espace sont deux figures égales, deux axes

4
x
O
x
et
x
O
x
'
'
1 1 1 2 2 2 sont deux figures égales ; de même: deux demi-droites. Deux plans de
l'espace sont deux figures égales.1 ci-jointe sont représentées deux figures qui sont les images
dans l'espace d'un même cube solide indéformable ; M un point du premier cube bleu et M' la
position de M après le déplacement de ce cube jusqu'au cube rouge. C'est ainsi qu'il est
possible d'envisager pour des solides de l'espace une coïncidence pont par point.
Figures 1 , 2, 3 et 4
II Orientation de l'espace. Repères orthonormés de même sens.
L'espace E1 est orienté lorsqu'on a choisi parmi les repères orthonormés2 de l'espace E (ou
simplement cartésiens) de désigner ceux qui sont de sens direct par la règle du bonhomme
d'Ampère rappelée ci-dessous sur la figure 2 : RAPPEL. Soit un repère cartésien R (OX,
OY, OZ) de l'espace et un "bonhomme" placé selon l'axe Z'OZ et regardant le plan XOY : si
le demi-axe OX est à sa main droite (figure 2) alors le repère est de sens direct, sinon il est dit
de sens rétrograde ou indirect. Orienter l'espace E c'est faire ce choix.
Théorème 1 (admis). On admet que ce procédé détermine une partition des repères
orthonormés de l'espace en deux classes ; ceux qui sont de sens direct et les autres qui sont
de sens rétrograde (ou indirect).
Si on considère uniquement les repères orthonormés dans l'espace orienté E, un plan
P( OIJ) de E est orienté de façon compatible par le choix d'une demi-normale dite positive.
Sur la figure 3 le repère orthonormé
ℜ
(
,
,
,
)
O
I
J
K
est de sens direct : le plan P = (OI J)étant
1 E qui a pour image l'espace physique est muni d'une distance : la distance euclidienne.
2Un repère orthonormé de l'espace est une " figure géométrique" indivisible. Les axes x'Ox, Y'Oy et Z'Oz sont
des parties de cette figure, notons surlces axes les points O, I, J, et K qui sont des points de cette figure. IL est
donc légitime d'envisager la relation d'égalité sur les repères orthonormés de l'espace.