Un solide de masse m = 100 g peut coulisser sans

ANNEE SCOLAIRE: 2008/2009 – CLASSE: 1S2 – DUREE: 2 HEURES
DEVOIR 2 DE SCICENCES PHYSIQUES
DEVOIR 2 DE SCICENCES PHYSIQUESDEVOIR 2 DE SCICENCES PHYSIQUES
DEVOIR 2 DE SCICENCES PHYSIQUES
1
© M. Wahab DIOP
Exercice 1: mouvement d’un solide sur un plan incliné
Un solide, de masse m=1,0 kg, part sans vitesse initiale du haut d’un plan incliné faisant un angle α=30° avec le
plan horizontale. Lorsque l’altitude du centre de gravité du solide a diminué de 2,0 m, la vitesse atteinte par le solide
est v=4,7 m·s
-1
.
1) En appliquant le théorème de l’énergie cinétique, évaluer l’intensité, supposée constante de la force de
frottement Å f qui s’exerce sur le solide.
2) Quelle devrait être la vitesse du solide en absence de frottement?
Exercice 2: mouvement d’un solide sur un plan incliné raccordé à une surface cylindrique
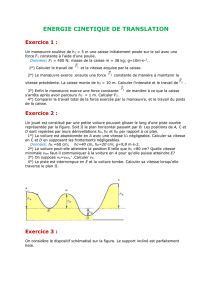
Une piste est constituée par un plan AB, de longueur ℓ=0,80 m,
incliné d’un angle α=60° sur l’horizontale et se raccordant
tangentiellement à une surface cylindrique BCD de rayon
r=O′B=0,50 m. L’extrémité D de la piste est au même niveau
que B.
Un solide supposé ponctuel de masse m=50 g est lâché, sans
vitesse initiale, au point A et glissent sans frottement le long de la
piste.
1) Déterminer les expressions littérales des altitudes des
points A et B. L’origine des altitudes est choisi en C, position la plus basse atteinte par le solide.
2) En appliquant le théorème de l’énergie mécanique, calculer la vitesse du solide lors de son passage en B, C et
D. (On donnera les expressions littérales avant toute application numérique)
Exercice 3: mouvement horizontal d’un pendule élastique
Un solide de masse m = 100 g peut coulisser sans frottement sur une tige horizontale. Il est relié à un
ressort de constante de raideur k.
A l’équilibre, son centre d’inertie est en O. Lorsqu’il oscille entre les points d’abscisses –a et +a (a valant
5,0 cm), sa vitesse de passage à la position d’équilibre est v
0
= 2,0 ms
-1
.
En appliquant les théorèmes liés à la variation de l’énergie mécanique :
1) Calculer la constante de raideur k du ressort.
2) Calculer la vitesse de passage au point d’abscisse
a
2
.
3) En réalité, la vitesse de passage au point d’abscisse
a
2
n’est que de 1,5 ms
-1
lorsque le centre
d’inertie du solide part (sans vitesse initiale) du point d’abscisse +a. Calculez l’intensité, supposée
constante, de la force de frottement.