supplémentaires, opposés par le sommet, alternes

DS de mathématiques
Nom : A 5°
Exercice 1 :
Compléter, si possible, les phrases ci-dessous en utilisant les expressions : « c omplémentaires,
supplémentaires, opposés par le sommet, alternes-internes, correspondants ».
(1)  AFB et  AFE sont des angles supplémentaires
(2)  ABE et  ACD sont des angles correspondants
(3)  AFE et  BFG sont des angles opposés par le sommet
(4)  EFG et  FGC sont des angles alternes-internes
(5)  BAF et  FAE sont des angles complémentaires
Exercice 2 :
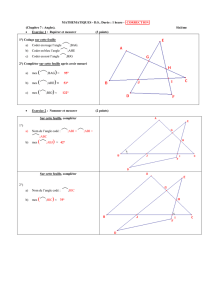
En utilisant les informations portées sur le schéma ci-dessous et le fait
que (NS) et (PQ) sont parallèles, calculer  MPQ,  MRN et  MQP. (Expliquer)
MPQ =  MNR = 60° car ils sont correspondants et (NS)// (PQ).
MRN=  SRQ = 80° car ils sont opposés par le sommet et donc égaux.
MQP=  SQP = 80° car ils sont alternes-internes et (NS)// (PQ).
Exercice 3 :
a) ABC est un triangle tel que  ABC = 70° et
BAC = 25° . Calculer  BCA .
BCA = 180° ‒ ( ABC +  BAC)
BCA = 180° ‒ (70° + 25°)
BCA = 180° ‒ 95°
BCA = 85°
b) EFG est un triangle rectangle en E tel que
EFG = 37°. Calculer  EGF.
EGF = 90° ‒  EFG
EGF = 90° ‒ 37°
EGF = 53°
c) KLM est un triangle isocèle en K tel que
LKM= 40°. Calculer  MLK.
MLK = (180° ‒  LKM) : 2
MLK = (180° ‒ 40°) : 2
MLK = 140° : 2
MLK = 70°
d) FGH est un triangle isocèle tel que FG = FH
et  FGH = 40°. Calculer  HFG.
HFG = 180° ‒ 2 ×  FGH
HFG = 180° ‒ 2 × 40°
HFG = 180° ‒ 80°
HFG = 100°
(2,5 pts)
(3 pts)
(4 pts)

Exercice 4 :
En utilisant les informations portées sur le schéma ci-contre et le fait
que (AG) et (FD) sont parallèles, calculer  ABC .
(Aide : Il faut d’abord déterminer les mesures des angles  BAC et  BCA.)
BED = 180° ‒  FAE = 180° ‒ 110° = 70° car BED et FAE sont supplémentaires
BAC =  BED = 70° car ils sont correspondants et (AG)// (FD)
BCA =  GCD = 50° car ils sont opposés par le sommet et donc égaux.
ABC = 180° ‒ ( BAC +  BCA)
ABC = 180° ‒ (70° + 50°)
ABC = 180° ‒ 120° = 60°
Exercice 5 :
a) Calculer l’angle  NPM.
MNP = 180° ‒ (  PNM +  NMP)
MNP = 180° ‒ (140° + 15°)
MNP = 180° ‒ 155°
MNP = 25°
b) Pourquoi (KL) et (MP) sont-elles parallèles ?
LPM =  KLP = 25°, les angles sont alternes-internes et égaux donc les droites (MP) et KL) sont parallèles.
Exercice 6 : Complète les définitions voir cours
a) Deus angles sont complémentaires si ………………………………………………………………………………………………
b) Deux angles sont adjacents si : ▪………………………………………………………………………………………………………
▪………………………………………………………………………………………………………
▪………………………………………………………………………………………………………
Exercice 7 :
a) Tracer un triangle ABC tel que AC = 7 cm,  ABC = 60° et  ACB = 40° .
b) Tracer un triangle TRS isocèle en S tel que SR = 4,5 cm,  TSR = 38° .
BAC = 180° ‒ (  ABC +  ACB)
BAC = 180° ‒ (60° + 40°)
BAC = 180° ‒ 100° = 80
(3 pts)
(2,5 pts)
(2 pts)
K
L
M
P
N
65°
25°
15°
140°
(3 pts)
A
C
B
S
R
T

DS de mathématiques
Nom : B 5°
Exercice 1 :
Compléter, si possible, les phrases ci-dessous en utilisant les expressions : « c omplémentaires,
supplémentaires, opposés par le sommet, alternes-internes, correspondants ».
(1)  ABE et  ACD sont des angles correspondants
(2)  AFB et  AFE sont des angles supplémentaires
(3)  EFG et  FGC sont des angles alternes-internes
(4)  BAF et  FAE sont des angles complémentaires
(5)  AFE et  BFG sont des angles opposés par le sommet
Exercice 2 :
a) ABC est un triangle tel que  ABC = 80° et
BAC = 45°. Calculer  BCA .
BCA = 180° ‒ ( ABC +  BAC)
BCA = 180° ‒ (80° + 45°)
BCA = 180° ‒ 125°
BCA = 55°
b) EFG est un triangle rectangle en E tel que
EFG = 36°. Calculer  EGF.
EGF = 90° ‒  EFG
EGF = 90° ‒ 36°
EGF = 54°
c) KLM est un triangle isocèle en K tel que
LKM= 35°. Calculer  MLK.
MLK = (180° ‒  LKM) : 2
MLK = (180° ‒ 35°) : 2
MLK = 145° : 2
MLK = 72,5°
d) FGH est un triangle isocèle tel que FG = FH
et  FGH = 50°. Calculer  HFG.
HFG = 180° ‒ 2 ×  FGH
HFG = 180° ‒ 2 × 50°
HFG = 180° ‒ 100°
HFG = 80°
Exercice 3 :
En utilisant les informations portées sur le schéma ci-dessous et le fait que (NS) et (PQ) sont parallèles,
calculer  MPQ,  MRN et  MQP. (Expliquer)
MPQ =  MNR = 60° car ils sont correspondants et (NS)// (PQ).
MRN =  SRQ = 80° car ils sont opposés par le sommet et donc égaux.
MQP =  SQP = 80° car ils sont alternes-internes et (NS)// (PQ).
(2,5 pts)
(3 pts)
(4 pts)

Même que sujet A
Exercice 4 :
En utilisant les informations portées sur le schéma ci-contre et le fait
que (AG) et (FD) sont parallèles, calculer  ABC .
(Aide : Il faut d’abord déterminer les mesures des angles  BAC et  BCA.)
Exercice 5 :
a) Calculer l’angle  NPM.
b) Pourquoi (KL) et (MP) sont-elles parallèles ?
Exercice 6 : Complète les définitions
a) Deus angles sont supplémentaires si ………………………………………………………………………………………………
b) Deux angles sont adjacents si : ▪………………………………………………………………………………………………………
▪………………………………………………………………………………………………………
▪………………………………………………………………………………………………………
Exercice 7 :
a) Tracer un triangle ABC tel que AC = 7 cm,  ABC = 60° et  ACB = 40° .
b) Tracer un triangle TRS isocèle en S tel que SR = 4,5 cm,  TSR = 38° .
(2,5 pts)
(3 pts)
K
L
M
P
N
65°
25°
15°
140°
(3 pts)
(2 pts)