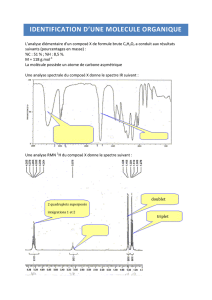
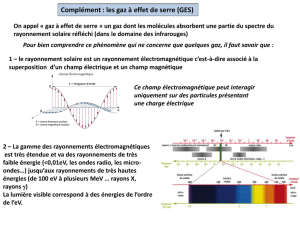
Chap. 9

Guy Collin, 2014-12-29
hn
Rotation
des molécules
polyatomiques
Chapitre 9

v = 0
v = 1
v = 2
h n
2014-12-29
Molécules polyatomiques
–Rotation pure
La molécule diatomique tourne sur elle-même
Quant est-il d’une molécule polyatomique ?
Est-ce que les lois, la quantification des niveaux
d’énergie, les règles de sélection sont conservées ?
L’utilisation de la mécanique quantique est-elle
toujours aussi féconde dans la détermination de la
structure moléculaire ?
Que se passe-t-il si l’on applique un champ
électrique important aux molécules en même temps
que l’excitation infrarouge ?

v = 0
v = 1
v = 2
h n
2014-12-29
Molécules polyatomiques
linéaires en rotation
Le modèle mécanique choisi pour représenter la
molécule diatomique peut s’étendre à ce cas.
La mécanique quantique permet d’obtenir les
niveaux d’énergie de rotation possibles.
La formule est identique à celle correspondant
aux molécules diatomiques :
E= (h2/8 p2I) J(J+1)
et le terme spectral est F(J) = BJ (J+1)
où B= h/ (8 p2c I).

v = 0
v = 1
v = 2
h n
2014-12-29
Molécules polyatomiques
linéaires en rotation
La nécessaire variation du moment dipolaire
permanent se traduit par une règle de sélection
qui est encore DJ= ± 1.
Puisqu’une valeur de B, permet d’obtenir une
longueur de liaison plusieurs liaisons, il faut
obtenir autant de valeurs de Bqu’il y a de
liaisons.
On mesure la constante Bpour des molécules
isotopiques : la substitution isotopique d’un
atome ne change pas la longueur de la liaison.

v = 0
v = 1
v = 2
h n
2014-12-29
Cas d’une molécule linéaire
triatomique
Exemple la molécule O=C=S
On observe le spectre de rotation pure 16O=12C=32S et
16O=12C=34S
On en déduit Bdans chaque cas, d’où Idans chaque cas.
En ayant 2 valeurs de I, on calcule les valeurs de r.
On peut ensuite vérifier ces valeurs de ren refaisant le
calcul sur un autre couple de molécules isotopiques
18O=12C=32S, 16O=13C=32S
etc.