version PowerPoint

SYSTEMES ISOTHERMES ET A COMPOSITION
CONSTANTE
Phénomènes de transferts
BILANS GLOBAUX DANS LE CAS
DE SYSTEMES ISOTHERMES ET A
COMPOSITION CONSTANTE
SOMMAIRE
Introduction
1- Conservation de la masse
2- Conservation de la quantité de mouvement
3- Bilan global d’énergie mécanique
4- Calcul des pertes par friction
2
PAGES
3
6
8
10
Nadine LE BOLAY
Une partie de ce document est issue du polycopié de cours de l’ENSIACET :
Phénomènes de transferts par J.P. Couderc, C. Gourdon et A. Liné
Application 1
Applications 2
Pertes par friction dans des tubes
rectilignes à section circulaire 10
Pertes par friction dans les accidents 17
Application 3
Récapitulatif 20
Pertes par friction pour l’écoulement autour d’objets 23
Non disponible
Non disponible
Non disponible
Non disponible
Non disponible

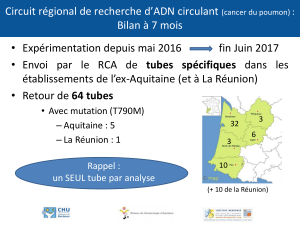
10
4 –CALCUL DES PERTES PAR FRICTION
Pertes par friction dans des tubes rectilignes à section circulaire
Ev= 2 <v>2f
L
D
^(19)
f = 1
4D L
Po–PL
1
2r<v>2(20)
Remarque :la définition du facteur de friction étant arbitraire, certains auteurs ont choisi de supprimer le
coefficient 1/4. On définit alors le facteur de Blasius par l’expression :
l=D
L
Po–PL
1
2r<v>2(22)
4- Calcul des
pertes par friction
(tubes)
Retour
sommaire
Les pertes par friction peuvent résulter de différents éléments que l’on décompose en
trois catégories :
-les longueurs droites de canalisations,
-tous les éléments qui raccordent ces longueurs droites (coudes, tés, élargissements ou
rétrécissements de section droite, etc...)ou viennent perturber les écoulements (robinets,
débitmètres, thermomètres, etc...) qu'on appelle des accidents de parcours ou des
singularités,
-les équipements spécifiques ou appareils de génie des procédés (réacteurs, filtres,
colonnes, etc...). Le calcul des pertes de charge à l'intérieur des appareils de génie des
procédés impose la mise en œuvre de méthodes spécifiques qui ne seront pas détaillées ici,
mais seront abordées dans les cours dédiés à ces appareils.
Pour calculer les pertes par friction dans les longueurs droites de canalisations on utilise,
habituellement, la relation :
où L est la longueur du tube, D, son diamètre et f, le facteur de friction de Fanning.Ce
facteur s’écrit selon l’expression dite de Fanning :
où l’indice o désigne l’entrée dans le tube, l’indice L, la sortie du tube et où la pression
motrice P regroupe les contributions de la pression et de la pesanteur selon la relation :
(21)P = p + rg h

11
(23)
f = 16
Re
Retour
sommaire
Une formule explicite a également été proposée dans la littérature :
Elle est applicable pour 104<Re < 107.
f = (3,6 log Re/7)-2 = (1,56 ln Re/7)-2 (25)
Cas de fluides newtoniens dans des tubes lisses
Pour des tubes idéaux, dont la surface interne est parfaitement cylindrique, sans aucune
imperfection, et à condition de se placer assez loin des extrémités du tube, l'expérience
permet d'observer que le facteur de friction est uniquement fonction du nombre de
Reynolds.
Lorsque le régime d’écoulement est laminaire (Re < 2100), la relation entre f et Re s’écrit :
(24)
f = 0,0791
Re1/4
Plusieurs expressions ont été proposées pour exprimer f en fonction de Re dans le cas où le
régime d’écoulement est turbulent (Re > 10 000). Parmi elles, on citera la loi de Blasius :
qui est valable pour 104<Re < 105.

12
Applications 2
On fait circuler de l’eau dans un tube de verre de 25 mm de diamètre interne muni de
deux prises de pressions espacées de 1 m. Pour différents débits d’eau variant entre
630 et 6000 L/h, on mesure les différentes valeurs de DP indiquées dans le tableau
ci-dessous.
Tracer l’évolution, en coordonnées logarithmiques, de DPen fonction du débit Q. En
déduire l’exposant de Q dans la relation DP = f(Q). Comparer cet exposant avec la
valeur théorique attendue.
DP (mbar)
Q (L/h) 630 1000 1500 2000 2500 3000 3500 4000 4500 5000
1,7 2,8 5,3 8,0 11,6 15,7 20,1 25,2 32,6 37,3
Applications 2
Retour
sommaire
Application 2.2
Application 2.1
Aide
Aide
De l’eau à 20 °C circule dans un tube de 7,5 cm de diamètre intérieur à un débit de
255 l/mn. Calculer le facteur de friction, f, àl’intérieur du tube.
Application 2.3
Aide
De l’eau à 20 °C circule entre deux réservoirs à un débit de 60 m3/h. Entre les
réservoirs sont placés deux types de tubes lisses, dont les diamètres internes sont
respectivement de 100 et 150 mm. Calculer les facteurs de frictions, f, relatifs à ces
deux tubes.

Remarque : Si on calcule le nombre de Reynolds pour les différents débits, on trouve qu’ils sont supérieurs à
10000 (de 14250 à 84750), sauf celui correspondant au débit de 630 L/h (Re = 9000). Le régime d’écoulement est
donc turbulent pour la majorité des débits, ce qui justifie la valeur de la pente de la droite.
13
Aides applications 2
Les points expérimentaux sont alignés, excepté celui correspondant au débit de 630 L/h.
Evolution de D P en fonction du débit
1
10
100
100 1000 10000
DP (mbar)
Q (L/h)
On détermine la pente de la droite, qui sera aussi l’exposant de Q dans la relation DP =
f(Q). Elle est égale à 1,68.
ATTENTION : Pour déterminer une pente en coordonnées logarithmiques, on calcule
D P doit être exprimé en Pascals et Q en m3/s
Ln( D P2) –Ln( D P1)
LnQ2–LnQ1
Pour déterminer la valeur théorique de la pente,d’après l’équation (20), on peut écrire
que DPest proportionnel à f.v2,c’est à dire à f.Q2.
En régime laminaire, d’après l’équation (23), fest proportionnel à v-1,c’est à dire à Q-1.DP
est alors proportionnel à Q1.
En régime turbulent, d’après l’équation (24), fest proportionnel à v-1/4,c’est à dire à
Q-1/4.DPest alors proportionnel à Q1,75.La valeur trouvée expérimentalement est proche
de cette valeur.
Retour
sommaire
Application 2.2
Application 2.1
Enoncé
Enoncé
A cet effet, on détermine tout d’abord la vitesse de circulation du fluide (= 0,962 m/s).
Pour calculer le facteur de friction, il faut connaître le régime d’écoulement afin de
choisir la relation convenable.
On calcule ensuite le nombre de Reynolds (= 72 150).
On est en régime turbulent.On calcule donc f avec la relation (24) (= 4,82.10-3)