Masse de zéros

Prise en compte
des données avec excès de zéros
Episode 2
Comment prendre en compte ?

Objectif
•Données de comptage
•Modèle « simple »
•Distribution de Poisson a priori
Comment prendre en compte
un excès de zéros ?

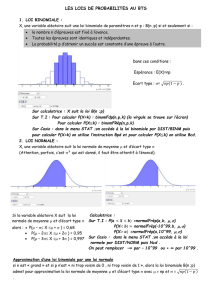
Les lois de probabilités discrètes
•Loi de Bernouilli
•Loi binomiale
•Loi géométrique
• …
•Loi de Poisson
•Loi Binomiale Négative

Loi de Poisson
•Loi des évènements rares
• Soit N le nombre d’évènements rares survenus dans un
intervalle de temps
N est une variable aléatoire dont la distribution est une
loi de Poisson
E(N) = λVar(N) = λ

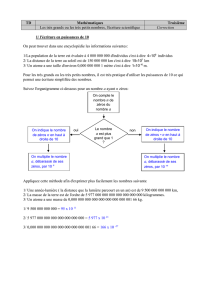
Loi Binomiale Négative
•«Pile-ou-face » tant que Pile n'est pas apparu k fois
Nombre de Pile = k
Probabilité de Pile = p ; probabilité de Face = 1-p = q
Nombre de lancers = L
•Le nombre L de lancers nécessaires pour gagner une
partie est une variable aléatoire, dont la distribution est
une distribution binomiale négative.
somme de variables géométriques indépendantes
(nb L de lancers jusqu’à 1ere apparition de Pile)