Document

1
ANIMATION
PAR
TRAJECTOIRES
Tomas Akenine-Möller, Eric Haines, Real-Time Rendering. A K
Peters, 2002, 835p.
Rick Parent, Animatique Algorithmes et techniques. Vuibert, Paris,
2003, 530p.
°Définition
°Choix de la courbe
°Contrôle du mouvement le long d’une courbe
°Interpolation de rotations représentées par des quaternions
°Suivi du trajet impliquant une modification de l’orientation de l’objet
°Lissage d’un trajet
°Détermination d’un trajet sur une surface
1.
2.

2
Définition
Toutes les caractéristiques d’une scène peuvent varier dans le temps :
- un point de référence sur un objet de la scène,
- la position de la caméra,
-la couleur d’un objet,
-la position d’une source lumineuse,
- etc.
Pour réaliser de telles animations, nous utilisons des trajectoires i.e.
des chemins qui représentent le parcours à suivre par un objet.
Outre les objets, il est également possible de lier une trajectoire à une
caméra ou à une source lumineuse.
Les trajectoires sont définies à l’aide de courbes paramétriques 3D :
C(u) (Cx(u), Cy(u), Cz(u)), u [0, 1].

3
Description du contexte auquel fait face l’animateur
Cette méthode permet de spécifier avec précision le mouvement
d’objets. Les attentes de l’animateur sont claires.
Très peu d’incertitude à propos des positions et orientations à produire,
l’ordinateur sert uniquement à calculer les valeurs réelles.
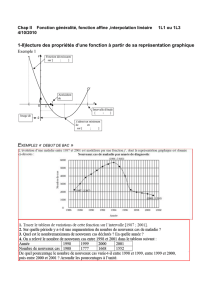
Choix de la trajectoire
Interpolation ou approximation ou techniques de points de contrôle
Courbe d’interpolation Courbe d’approximation ou
d’ajustement
Échantillon de points rapprochés
de la courbe
Positions effectives par lesquelles
la courbe doit passer.

4
Critères de choix de la trajectoire
Courbe de Bézier
Technique de points de contrôle
Liste de points permettant de
contrôler la forme de la courbe
Complexité de la trajectoire
Complexité (degré) Moins rapide est l’évaluation des
polynômes.
Meilleur choix : les polynômes cubiques par morceau.
Fournissent un tracé suffisamment régulier tout en procurant
suffisamment de flexibilité pour satisfaire aux contraintes de
continuité.
Un polynôme d’ordre supérieur n’offre pas d’avantages significatifs.

5
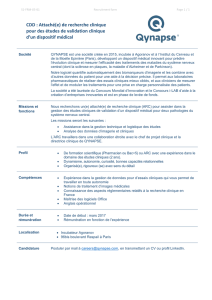
Critères de choix de la trajectoire
Continuité de la courbe composée (courbe par morceaux)
aux points de jonction entre segments adjacents
La régularité de la courbe obtenue est une considération importante.
Le nombre de dérivées continues de l’équation de la courbe.
Discontinuité positionnelle Continuité d’ordre 0
mais pas tangentielle
Continuité d’ordre 0 et 1
(en animation, cela est suffisant habituellement)