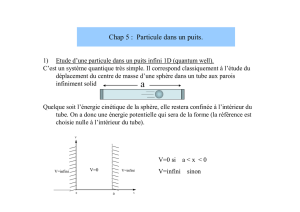
Équation de Schrödinger dans un potentiel uniforme par morceaux

Équation de Schrödinger dans un potentiel uniforme par
morceaux
PC Lycée Dupuy de Lôme
E. Ouvrard (PC Lycée Dupuy de Lôme) Mécanique quantique 1 / 23

1Recherche des solutions
Postulat
2Puits de potentiel infini
Pulsations propres
Similitudes avec la corde
Énergie minimale
Mode fondamental
Conséquence de l’inégalité d’H.
Densité de probabilité pour 1 mode
Superposition d’états stationnaires
3Puits de potentiel de profondeur finie
Solutions hors du puits
Si E>V0
Si E<V0
Solutions dans puits
Exploitation des CAL
Principe de symétrie
Interprétation graphique
Abaissement des niveaux d’énergie
Largeur effective
Double puits
E. Ouvrard (PC Lycée Dupuy de Lôme) Mécanique quantique 2 / 23

Recherche des solutions Postulat
Forme générale des solutions
Dans chaque domaine où le potentiel est uniforme ( et indépendant
du temps), les solutions sont stationnaires
Ψ(x, t)=ϕ(x).e−i. E.t
̵
h
On doit vérifier en tout point la continuité de la fonction d’onde
Équation de Schrödinger pour un état stationnaire
ϕ(x)devant vérifier l’équation de Schrödinger, il en résulte
−
h2
2.m .∂2ϕ(x) ∂x2+V(x).ϕ(x)=E.ϕ(x)
E. Ouvrard (PC Lycée Dupuy de Lôme) Mécanique quantique 3 / 23

Puits de potentiel infini Pulsations propres
x
V(x)
E>0
0a
E<<V0
→
x
V(x)
→∞→∞
E>0
0a
Régions interdites
Dans les régions de l’espace où le potentiel est infini, la probabilité de
présence de la particule quantique est nulle.
ϕ(x>a=0
E. Ouvrard (PC Lycée Dupuy de Lôme) Mécanique quantique 4 / 23

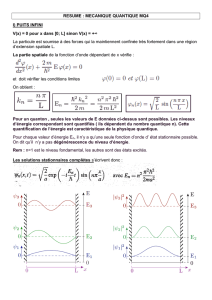
Puits de potentiel infini Pulsations propres
Proposer la forme générale pour ϕ(x)
Exploiter les CAL
En déduire les modes possibles
Normaliser la fonction d’onde
Fonction d’onde pour un puits infini
ϕ(x<a=2
a.e−i. En
̵
ht.sinn.π.x
aavec En=n2.π2.
h2
2.m.a2
L’énergie dans un puits de potentiel infini est donc quantifiée.
E. Ouvrard (PC Lycée Dupuy de Lôme) Mécanique quantique 5 / 23