Δ 2 Δ 2

P9 - Activité 2: Mouvement d’un mobile et 2
ème
loi de Newton
Objectifs :
- Déterminer graphiquement les vecteurs vitesse et accélération instantanée en différents points de la trajectoire
d’un mobile.
- Exploiter les résultats dans le cadre d’une approche qualitative puis quantitative de la seconde loi de Newton.
Expérience :
Sur un plan incliné d’un angle α, un mobile autoporteur
(la force de frottement solide est quasiment nulle) est
lancé avec une vitesse initiale non nulle dans le plan.
On donne la masse du mobile: m = 610g.
Les positions successives du palet sont représentées
tous les τ = 40 ms (voir enregistrement)
1- Inventaire des forces extérieures s’exerçant sur le mobile
- Faire l’inventaire des forces qui s’exercent sur le mobile autoporteur lorsqu'il est posé sur le plan incliné.
- Représenter ces forces sur un schéma (un schéma en coupe est plus adapté) et en déduire la valeur de la
résultante, sachant que le solide reste sur le plan incliné pendant toute l'expérience.
2- Construction des vecteurs vitesse instantanée du centre d’inertie du mobile
- Calculer les valeurs de la vitesse instantanée du centre d’inertie du mobile au position G
4
, G
6
, G
9
, G
11
, G
16
et G
18
.
- Tracer soigneusement les vecteurs vitesse correspondant en prenant l’échelle 1 cm pour 0,1 m.s
-1
.
Rappels sur l’approche qualitative de la seconde loi de Newton (cours de 1°S)
Dans un référentiel supposé galiléen, la résultante des forces extérieures appliquées à un solide et la variation du
vecteur vitesse de son centre d’inertie ont même direction et même sens.
3- Construction des vecteurs variation de vitesse
- Construire les vecteurs variation de vitesse
5
v∆
,
10
v∆
et 17
v∆ aux positions G
5
, G
10
et G
17.
.
- L’approche qualitative de la seconde loi de Newton est-elle vérifiée ?
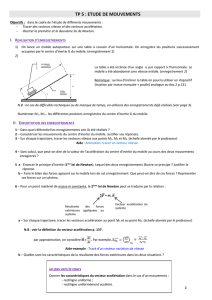
Construction du vecteur accélération:
Pour construire, à partir d’un enregistrement, le vecteur accélération du mobile au point M
2
(position du mobile à la
date t
2
) il faut en déterminer les caractéristiques (la direction, le sens et la valeur):
Pour cela on construit le vecteur variation de vitesse )(tv∆
2
au point M
2
en considérant deux points M
1
et M
3
,
situés de part et d’autre du point M
2
et le plus rapprochés de lui (voir activité).
- le point d’application du vecteur accélération est le point M
2
.
- la direction et le sens du vecteur accélération au point M
2
est celle de )(tv∆
2
en ce point
- la valeur du vecteur accélération au point M
2
(à la date t
2
) est assimilée à l'accélération moyenne mesurée entre
les points M
1
et M
3
. Elle est donnée par l'expression :
13
)
2
(
)
2
(tt tV ta −
∆
=
et s'exprime en m.s
-2
- on trace un segment fléché dont la longueur est proportionnelle à la valeur a(t
2
) en utilisant l’échelle des
accélérations donnée. Par exemple, si l’échelle des vitesses est 1cm pour 2 m.s
–2
et que l’on trouve a = 5 m.s
– 2
,
on trace alors un segment fléché de longueur 2,5 cm.
4- Tracé des vecteurs accélération instantanée
- Des tracés précédents, déduire les valeurs des accélérations a
5
, a
10
, a
17
.
- Tracer les vecteur accélération 5
a, 10 a et 17
a en prenant l’échelle 1 cm pour 0,2 m.s
-2
- Calculer le produit m.a (masse x accélération en USI) pour chacun des points étudiés. Comparer à la valeur de la
résultante des forces appliquées au système et conclure.
h = 9,
0
cm
l =
90
cm
α
αα
α
M
1
M
3
•
M
2
)
2
(ta