Guides à cristaux photoniques à fente en régime d`ondes

Guides à cristaux photoniques à fente en régime d’ondes lentes
pour l’optique non-linéaire
Charles CAËR, Xavier LE ROUX, Eric CASSAN
Institut d’Electronique Fondamentale (IEF)
Département de photonique
Université Paris-Sud, CNRS UMR 8622
Bât. 220, Centre scientifique d’Orsay
91405 ORSAY – France
Email : [e-mail]
Résumé
Nous présentons un nouveau design de guides à cristaux
photoniques à fente large en filière SOI basé sur une
structuration de la fente. Ce type de dispositif permet
d’atteindre de très faibles vitesses de groupe (inférieures à
c/40) sur une bande passante de quelques nanomètres. Cela
donne l’opportunité de réaliser des dispositifs ayant une très
forte interaction lumière-matière. Par ailleurs, le
remplissage de la fente par un matériau fortement non
linéaire permet d’obtenir des effets optiques non linéaires
très intenses grâce au très fort confinement optique dans la
fente.
Nous présenterons des résultats d’ingénierie de
dispersion par méthodes d’onde plane (PWE) et de
différences finies dans le domaine temporel (FDTD, puis des
résultats expérimentaux sur la transmission des ces
structures.
1. Introduction
Les guides d’ondes à cristaux photoniques sont de
prometteurs dispositifs pour le traitement tout optique de
l’information et l’étude des interactions lumière-matière,
grâce au régime d’ondes lentes [1-2].
Cependant, les pertes de propagation en régime
d’ondes à faibles vitesses de groupe, principalement dues
à la rétrodiffusion de la lumière en raison du désordre
inhérent à la fabrication, et à la distorsion brutale du pulse
générée par la très forte dispersion d²ω/dk², limitent la
généralisation de ces guides, même si le problème a été
partiellement résolu par l’ingénierie de dispersion du
mode guidé. Cette ingénierie de dispersion consiste à
modifier la géométrie du guide (rayons des trous,
écartement de rangées de trous, …) afin d’ajuster la pente
de la bande guidée.
Le renforcement local du champ électrique est
particulièrement bénéfique pour les interactions non-
linéaires. Des phénomènes exploitant la susceptibilité
non-linéaire d’ordre χ
(3)
du silicium tels que l’auto-
modulation de phase, la génération de troisième
harmonique ou le mélange quatre ondes ont été démontrés
[3]. Cependant, les phénomènes non-linéaires sont limités
dans le silicium par les phénomènes d’absorption multi-
photons ou de porteurs libres.
Il est possible de s’affranchir de ces limitations par
l’introduction d’une fente de taille sub-longueur d’onde
qui permet de fortement confiner la lumière dans le
matériau de bas indice, en raison de la très forte
discontinuité du champ électrique à l’interface [4]. En
remplissant la fente par des polymères fortement non-
linéaires, il est possible d’exacerber les phénomènes non-
linéaires d’ordre 2 et 3 [4].
Le régime d’ondes lentes pour des cristaux
photoniques à fente apparaît alors très prometteur pour
l’optique non-linéaire, car tirant profit de la très forte
intensité résultant à la fois à de la compression spatiale du
pulse et du confinement sub-longueur d’onde dans la fente
[5].
Ce travail s’inscrit dans ce contexte et propose une
méthode pour réaliser l’ingénierie de dispersion des
guides à cristaux photoniques à fente. Une nouvelle
méthode basée sur la structuration de la fente en peigne
(fig. 1) permet d’obtenir un indice de groupe (n
g
=c/v
g
)
constant sur quelques nanomètres et un très fort
confinement dans la fente, là où elle se rétrécit.
2. Calcul de la courbe de dispersion
L’ingénierie de dispersion de la structure se fait par la
méthode d’onde plane. Il s’agit d’optimiser le diagramme
de bande du cristal en modifiant les paramètres
géométriques du cristal afin d’obtenir un indice de groupe
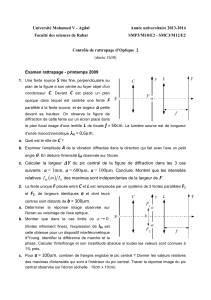
Figure 1. Image au microscope électronique à
balayage d’un guide à cristal photonique et à fente
structurée

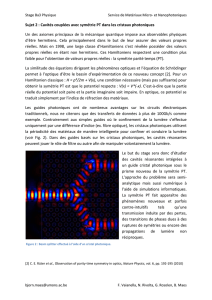
Figure 2. Schémas représentant la cellule utilisée pour
le calcul par méthode d’ondes planes
constant sur plusieurs nanomètres. Le diagramme de
bande est calculé par le logiciel MPB. La méthode
d’optimisation est présentée en détail dans la réf. [6]. La
structure simulée représentée sur la figure 2 consiste en un
cristal photonique en technologie SOI (silicium sur
isolant). Le film de silicium a une épaisseur de 260nm et
un indice de réfraction de 3,48. Il repose sur 2µm de silice
enterrée d’un indice de 1,44 et est recouvert d’une couche
de polymère d’un indice de 1,6 qui remplit à la fois les
trous et la fente. Le paramètre de maille a vaut 400nm et
le rayons des trous r vaut 120nm afin d’assurer une large
bande interdite pour une polarisation TE.
En travaillant à une largeur de fente donnée, les trois
paramètres décrivant le peigne dy, dx et l offrent trois
degrés de liberté pour obtenir l’indice de groupe désiré.
Faire varier la position des trous adjacents à la fente ainsi
que leurs rayons permet d’ajuster plus précisément la
pente de la bande exploitée.
Avec le jeu de paramètres suivants exprimés en
fonction du paramètre de maille a: W1,25, W2=0,65√3a,
W3=0,45√3a, W
slot
=0,35a, dx=0,5a, dy=0,4a, l=0,75,
r
1
=0,28a, r
2
=0,38a, on obtient un indice de groupe moyen
de 45 sur une bande passante de 4,5nm [7]. Par ailleurs, il
apparaît qu’à l’endroit où la fente se rétrécit, le
confinement du champ est très fortement accru, comme
l’on peut le voir sur la figure 4 d).
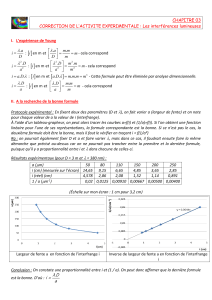
Figure 3. a) Diagramme de bande du cristal
photonique optimisé (courbe verte). b) Indice de
groupe correspondant. c) Vue en coupe de l’intensité
du champ électrique ε|E|² au point k=0.45. d) Carte
d’intensité dans le plan z=0.
3. Analyse fréquentielle
L’analyse fréquentielle du cristal photonique optimisée
se fait au moyen par la méthode des différences finies
dans le domaine temporel (FDTD) au moyen du logiciel
MEEP. Cette analyse est nécessaire afin d’étudier le
couplage entre un guide réfractif d’accès et le cristal. Le
calcul peut se faire en deux dimensions car seuls les
modes situés sous la ligne de lumière sont exploités.
L’indice du silicium est alors approximé par son indice
effectif (n
eff
~2,83). Le calcul en 2D représente un gain de
temps très appréciable et permet de simuler le
comportement d’un dispositif complet, la FDTD étant
extrêmement consommatrice en ressources de calcul.
Le dispositif est constitué de deux guides réfractifs
monomodes d’entrée/sortie de 400nm de largeur,
auxquels sont couplés des guides à fente servant d’accès
au cristal photonique. La conversion de mode grâce à des
tapers assurant une adaptation adiabatique entre le guide
réfractif et le guide à fente. L’entrée dans le cristal
photonique se fait grâce à deux régions de transitions qui
servent d’interfaces entre les modes lents et modes
rapides, afin de minimiser les pertes par réflexion. Ces
transitions sont faites en étirant légèrement dans l’axe de
propagation le paramètre de maille du cristal [8]. La
longueur totale de la cellule est 177,5µm, le cristal
photonique étant long de 88,7µm.
La structure est excitée par une source gaussienne
d’une largeur spectrale de 500nm centrée à 1550nm. Deux
capteurs sont placés en entrée et en sortie du dispositif et
possèdent tous deux une résolution spectrale de 50pm. La
fenêtre temporelle est de 70ps, temps suffisamment long
pour les composantes d’indice de groupe élevé aient le
temps d’atteindre le capteur de sortie.
Figure 4. Haut: indices de groupe calculés par méthode
d’onde plane (rouge) et FDTD (bleu). Bas : spectre de
transmission correspondant.
Les paramètres du cristal photonique simulé donnent
un indice de groupe de 45 sur une bande passante de 5nm
calculé par méthode d’onde plane. Le calcul de l’indice de
groupe en FDTD se fait par extraction des franges de
Fabry-Perot en bord de bande (fig. 4). Cela permet de
remonter à un indice de groupe de 35 sur une bande
passante de 6nm [7]. La transmission en bord de bande à
-12dB montre un assez faible niveau de pertes dans le
cristal.
La méthode FDTD permet donc de donner une bonne
estimation qualitative du spectre de transmission et de
manipuler les ondes lentes.

4. Fabrication et caractérisation
L’échantillon a été fabriqué dans la centrale
technologique de l’IEF (CTU-Minerve). Des wafers de
SOITEC avec 260nm d’épaisseur de silicium et 2µm de
silice enterrée ont été masqués par de la résine électro-
sensible ZEP-250. Les motifs ont été transférés par
lithographie électronique 80kV puis gravés par ICP
(Inductively Coupling Plasma) en utilisant du gaz SF
6
. Les
faces latérales de la puce ont été clivées après nettoyage
de la résine.
Les dispositifs ont été caractérisés par un laser
accordable à large spectre allant de 1390 à 1640nm. La
lumière est ensuite filtrée par un contrôleur de polarisation
afin d’obtenir des modes TE, avant d’être injecté dans la
puce via une fibre monomode micro-lentillée à maintien
de polarisation. Les entrées-sorties de l’échantillon sont
des guides totalement gravés de 3µm convertis en guides
de 400nm de large par des tapers de 0,8mm de long. Puis
d’autres tapers assurent la transition vers les guides à fente
avant de pénétrer dans les cristaux photoniques.
En sortie, la lumière est collectée par un objectif de
microscope puis envoyée à un analyseur de spectre.
Toutes les mesures sont faites après dépôt d’une goutte de
liquide d’indice de réfraction 1,46 afin de symétriser la
structure. Le spectre de transmission représenté sur la
figure 5 montre un bord de bande à 1488,5nm.
L’extraction de l’indice de groupe donne un indice de
groupe moyen d’environ 40 sur une bande passante de
3nm [7], ce qui démontre la possibilité de réaliser de
l’ingénierie de dispersion des cristaux photoniques à fente
structurée en peigne.
Figure 5. a) Diagramme de bande du cristal photonique optimisé
(courbe verte). b) Indice de groupe correspondant. c) Vue en
coupe de l’intensité du champ électrique ε|E|² au point k=0.45. d)
Carte d’intensité dans le plan z=0.
5. Conclusion
Nous avons montré une méthode permettant de réaliser
de l’ingénierie de dispersion des guides à cristaux
photoniques à fente en structurant celle-ci sous forme de
peigne. L’optimisation géométrique par méthode d’onde
plane a permis d’obtenir un indice de groupe de 45 sur
une bande passante de 4,5nm.
La méthode FDTD nous a ensuite permis de valider
l’ingénierie de dispersion, d’étudier le couplage avec des
guides réfractifs et de comprendre la propagation de la
lumière grâce au spectre de transmission.
Figure 6. Représentation du montage expérimental
Enfin, nous avons fabriqué et caractérisé des
dispositifs qui nous ont permis d’obtenir
expérimentalement un indice de groupe de 40 sur une
bande passante de 3nm, ce qui constitue la première
démonstration expérimentale d’ingénierie de dispersion
d’un guide à cristal photonique et à fente.
Ce type de dispositif ouvre des perspectives
prometteuses en optique non-linéaire intégrée.
Références
[1] T. Baba, "Slow light in photonic crystals", Nature Photonics
12 (2008) pp 125-128.
[2] T. F. Krauss, “Slow light in photonic crystal waveguides”,
Journal of Phyics D: Applied Physics 40 (2007) pp 2666-
2670.
[3] C. Monat, B. Corcoran, D. Pudo, M. Ebnali-Heidari, C.
Grillet, M. D. Pelusi, D. J. Moss, B. J. Eggleton, T. P.
White, L. O’Faolain, T. F. Krauss, “Slow Light Enhanced
Nonlinear Optics in Silicon Photonic Crystal Waveguides”,
IEEE Journal of Selected Topics in Quantum Electronics 16
(2010) pp 344-356.
[4] J. Leuthold, W. Freude, J.-M. Brosi, R. Baets, P. Dumon, I.
Biaggio, M. L. Scimeca, F. Diederich, B. Frank, C. Koos,
“Silicon Organic Hybrid Technology - A Platform for
Practical Nonlinear Optics”, Proceedings of the IEEE 97
(2009) pp 1304-1316.
[5] A. Di Falco, L. O’Faolain, T. F. Krauss, “Dispersion control
and slow light in slotted photonic crystal waveguides”,
Applied Physics Letters 92 (2008) pp 083501-1-3.
[6] C. Caer, X. Le Roux, V. K. Do, D. Marris-Morini, N. Izard,
L. Vivien, D. Gao, E. Cassan, “Dispersion Engineering of
Wide Slot Photonic Crystal Waveguides by Bragg-like
Corrugation of the Slot”, IEEE Photonics Technology
Letters 23 (2011) pp 1298-1300.
[7] C. Caer, X. Le Roux and E. Cassan, "Enhanced Localization
of Light in Slow Light Slot Photonic Crystal Waveguides", à
paraître.
[8] J.-P. Hugonin, P. Lalanne, T. P. White, T. F. Krauss,
“Coupling into slow-mode photonic crystal Waveguides”,
Optics Letters 32 (2007) pp 2638-2640.