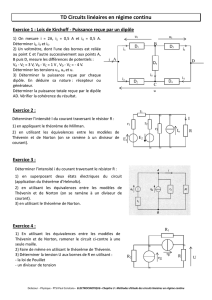
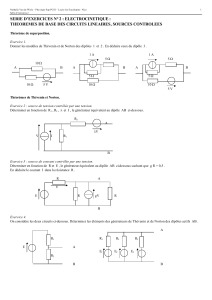
TD n°5

1
HLPH312
Physique Concours
Responsable : Y. LACHAUD
EXAMEN
CIRCUITS ELECTRIQUES
(Durée de l'épreuve 1h30)
Calculatrice non autorisée.
Il sera tenu compte dans la correction, du respect des notations proposées dans l’énoncé, de la
clarté des explications fournies et de la correction de l’expression écrite.
Dans l'énoncé du problème, les grandeurs réelles positives sont notées en caractère droit, les
grandeurs algébriques en caractère italique, les grandeurs complexes sont soulignées.
I. Questions de cours
On considère le dipôle D représenté sur la figure 1 ci-contre. Ce
dipôle est traversé par un courant I. Par ailleurs, les potentiels
des bornes A et B mesurés par rapport à celui de la masse
(représentée ci-contre par le symbole ) sont respectivement
U(A) et U(B).
Les conventions de mesure du courant I et des potentiels U(A) et U(B) sont représentées sur la
figure 1.
I.1. Rappeler la définition du courant électrique I représenté sur la figure 1.
I.2. Quelle est la quantité de charge électrique dq qui pénètre par la borne A du dipôle
D entre les instants t et t+dt ?
Quelle est la quantité de charge électrique dq’ qui sort par la borne B du dipôle D entre les
instants t et t+dt ?
I.3. Rappeler la définition du potentiel électrique U(A) représenté sur la figure 1.
I.4. Quelle est la quantité d’énergie électrique dE qui pénètre par la borne A du dipôle
D entre les instants t et t+dt ?
Quelle est la quantité d’énergie électrique dE’ qui sort par la borne B du dipôle D entre les
instants t et t+dt ?
I.5. Déduire de la question précédente la quantité d’énergie électrique dW reçue par le
dipôle D entre les instants t et t+dt.
On définit la tension U par la différence des potentiels entre les bornes A et B :
U = U(A) – U(B).
I.6. Utiliser cette tension U pour simplifier l’écriture de dW. En déduire la signification
physique de la grandeur P = U I.
…/…

2
I.7. Rappeler la définition d’un nœud dans un circuit électrique.
I.8. Enoncer la loi des nœuds.
I.9. Rappeler la définition d’une maille dans un circuit électrique.
I.10. Enoncer la loi des mailles.
II. Associations de dipôles
II.1. Rappeler la relation caractéristique d’un résistor de résistance R parcouru par un
courant I et ayant une différence de potentiel U entre ses bornes. On précisera sur un schéma
les conventions retenues pour les mesures de I et de U.
On dispose de 2 résistors de résistance individuelle R1 et R2.
II.2. Démontrer à partir des lois fondamentales de l’électrocinétique le théorème
d’équivalence suivant :
II.3. Donner sans démonstration la valeur de la résistance équivalente, notée RE, du
résistor équivalent à l’association parallèle de deux résistors de résistances R1 et R2 :
On dispose maintenant de 3 résistors identiques de résistance individuelle R.
II.4. Quelles sont les quatre différents dipôles que l’on peut réaliser en connectant de
diverses manières ces trois résistors ? Pour répondre à cette question, on dessinera
explicitement ces quatre associations.
II.5. En utilisant les équivalences graphiques des questions II.2 et II.3 aux quatre
associations précédentes, déterminer la valeur de la résistance de chacune de ces quatre
associations.
Une source réelle de courant (source de Norton) est constituée
par l’association parallèle d’une source idéale de courant
(courant électromoteur C) et d’un résistor (résistance R)
comme indiqué sur le schéma ci-contre.
II.6 Etablir la relation courant-tension pour cette source de Norton si l’on mesure les
grandeurs électriques u et i avec les conventions fixées sur ce schéma.
Une source réelle de tension (source de Thévenin) est
constituée par l’association série d’une source idéale de
tension (force électromotrice E) et d’un résistor (résistance R’)
comme indiqué sur le schéma ci-contre.
II.7 Etablir la relation courant-tension pour cette source si l’on mesure les deux
grandeurs électriques u et i avec les conventions fixées sur ce schéma.
II.8 Trouver les conditions que l’on doit imposer entre les quatre paramètres qui
caractérisent les sources réelles de Norton [R ; C] de la question II.6 et de Thévenin [R’; E] de
la question II.7, pour que ces deux dipôles soient électriquement équivalents.
…/…

3
II.9 Déterminer par la méthode des équivalences graphiques les paramètres [X ; Y]
caractéristiques de l'unique source de Norton équivalente à l’association série de deux sources
de Norton [R ; C] & [R’; C’] dessinée ci-dessous :
II.10 Déterminer par la méthode des équivalences graphiques les paramètres [X’ ; Y’]
caractéristiques de l'unique source de Thévenin équivalente à l’association parallèle de deux
sources de Thévenin [R ; E] & [R’; E’] dessinée ci-dessous :
III. Théorèmes de Thévenin et Norton
On considère dans cet exercice un dipôle (AB) constitué exclusivement par l’association de
dipôles affines (résistors, sources idéales de courant et de tension) :
On rappelle ci-dessous les contenus des théorèmes de Thévenin et de Norton :
« Toute association de dipôles affines est équivalente à une unique source de Thévenin de
paramètres [R ; ETH]. La force électromotrice ETH est égale à la tension mesurée au voltmètre
idéal branché aux bornes de l’association et la résistance interne R est égale à la résistance de
l’association passivée mesurée à l’ohmmètre idéal. »
« Toute association de dipôles affines est équivalente à une unique source de Norton de
paramètres [R ; CNO]. Le courant électromoteur CNO est égal au courant mesuré à
l’ampèremètre idéal branché aux bornes de l’association et la résistance interne R est égale à
la résistance de l’association passivée mesurée à l’ohmmètre idéal. »
III.1 Dessiner la source de Thévenin [R ; ETH] équivalente au dipôle (AB).
III.2 Rappeler la définition d’un voltmètre idéal.
III.3 Dessiner le circuit électrique que l’on doit réaliser avec le dipôle (AB) pour
mesurer la force électromotrice ETH.
III.4 Dessiner la source de Norton [R ; CNO] équivalente au dipôle (AB).
III.5 Rappeler la définition d’un ampèremètre idéal.
III.6 Dessiner le circuit électrique que l’on doit réaliser avec le dipôle (AB) pour
mesurer le courant électromoteur CNO.
III.7 Montrer que si l’on ne dispose que d’un voltmètre idéal et d’un ampèremètre idéal,
il est malgré tout possible de déterminer la résistance interne R de l’association. On exprimera
R en fonction de ETH et CNO.
…/…

4
Le voltmètre utilisé par l’expérimentateur n’est en réalité pas idéal, il possède en fait une
résistance interne non infinie égale à RV.
III.8 Exprimer la tension U effectivement mesurée par ce voltmètre réel lorsqu’on
réalise le circuit de la question III.3. On exprimera la tension U en fonction de ETH, CNO et RV.
L’ampèremètre utilisé par l’expérimentateur n’est pas lui non plus idéal, il possède en réalité
une résistance interne non nulle égale à rA.
III.9 Exprimer le courant I effectivement mesuré par cet ampèremètre réel lorsqu’on
réalise le circuit de la question III.6. On exprimera le courant I en fonction de ETH, CNO et rA.
III.10 Montrer que si l’on ne dispose que d’un voltmètre réel (de résistance interne RV
connue) et d’un ampèremètre réel (de résistance interne rA connue), il est malgré tout possible
de déterminer les caractéristiques de la source de Thévenin ou de Norton équivalente au dipôle
(AB). Pour répondre à cette question, il suffit d’exprimer les grandeurs ETH et CNO en fonction
de U, I, RV et rA.
IV. Etude d’un circuit
On considère le circuit représenté ci-contre dans
lequel la source idéale de tension délivre une
f.e.m. e(t) = E sin(t) et la source idéale de
courant délivre un c.e.m. c(t) = C cos(t) :
IV.1 Montrer que la tension u(t) aux bornes de la bobine obéit à une équation
différentielle de la forme suivante :
𝑑𝑢(𝑡)
𝑑𝑡 + ω0 𝑢(𝑡) = 1 2 𝑑𝑒(𝑡) 𝑑𝑡 + R 𝑑𝑐(𝑡) 𝑑𝑡 .
On exprimera 0 en fonction de L et R.
Dans un premier temps, on passive les deux sources d’énergie du circuit.
IV.2 Dessiner le nouveau circuit électrique obtenu. On notera u0(t) la tension présente
aux bornes de la bobine dans ce nouveau circuit.
IV.3 Donner l’expression générale de cette solution libre u0(t).
Dans un deuxième temps on active la source idéale de tension (source de courant passivée).
IV.4 Dessiner le nouveau circuit électrique obtenu. On notera u1(t) la tension présente
aux bornes de la bobine en régime sinusoïdal permanent.
IV.5 Exprimer la tension complexe de régime permanent u1(t), en fonction de e(t).
IV.6 En déduire que : u1(t) = ½  E [0 cos(t) +  sin(t)] / [] .
Dans un troisième temps on active la source idéale de courant (source de tension passivée).
IV.7 Dessiner le nouveau circuit électrique obtenu. On notera u2(t) la tension présente
aux bornes de la bobine en régime sinusoïdal permanent.
IV.8 Exprimer la tension complexe de régime permanent u2(t), en fonction de c(t).
IV.9 En déduire l’expression de u2(t) en fonction de , 0, R et C.
Finalement, on active simultanément les deux sources d’énergie.
IV.10 Montrer que la tension u(t) peut s’écrire : u(t) = u0(t) + u1(t) + u2(t).
__________________