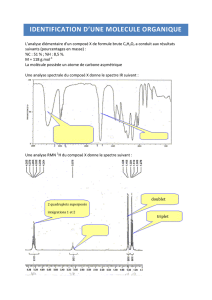
Spectroscopie infrarouge

Spectroscopie infrarouge
Le principe de cette spectroscopie est tout à fait semblable à celui de la spectrophotométrie dans le visible étudiée en TP.
L’examen des radiations absorbées par l’échantillon permet d’identifier les transitions entre niveaux d’énergie et d’en déduire des
informations sur la structure de la molécule. En UV/visible, les radiations absorbées correspondent à des transitions entre niveaux
d’énergie électroniques. Dans l’infrarouge, les énergies mises en jeu sont principalement des énergies de vibration (infrarouge
proche) voire de rotation (infrarouge lointain).
I Modes de vib ration d’une molécule organique
1 Généralités
a Absorption de l’onde électromagnétique
Les longueurs d’onde absorbées vont de 2.5 µ à 25 µ. On préfère utiliser l’inverse de la longueur d’onde 1
λ
=
ν
c
appelé nombre d’onde et exprimé usuellement en cm
-1
(on utilise souvent de façon impropre l’appellation “fréquence”). Les spectres
IR sont donc tracés dans l’intervalle maximal [ 400, 4000 ] (cm-1 ), la grandeur portée en ordonnée étant la transmittance T =
I
I0 ou
l’absorbance (ou densité optique) d = log
I0
I
, I étant l’intensité transmise par l’échantillon et I
0
l’intensité transmise par la référence.
Rappel : Loi de Beer-Lambert
Sur une longueur dx, l’intensité dI absorbée est proportionnelle à I et C, concentration de l’espèce absorbante, soit dI = - k C I
dx d’où d = log = k C l ou l est la longueur traversée par le faisceau.
On présente la loi sous la forme :
d = ε l C
ε est le coefficient d’extinction molaire du composé (il dépend de λ , T et du solvant). Cette loi est valable pour les solutions
diluées et dans ces conditions les densités optiques sont additives.
b Exemple de spectre
Spectre d’absorption IR d’une cétone
4000
3000 2000 1800 1600 1400 1200 1000
100
0
cm-1
Transmittance

On voit dans ce spectre des bandes d’absorption à 2950 cm
-1
, 1720 et dans la zone 1450-1100 cm
-1. Ces bandes
correspondent aux vibrations des liaisons CH, C=O, CH et CC de la cétone.
Le spectre peut être obtenu par balayage en longueur d’onde, en utilisant un monochromateur, ou dans les appareils récents
par analyse de Fourier du signal transmis.
c Modèles utilisés
L’absorption infrarouge par la molécule met en jeu deux types de vibration :
- vibration d’élongation correspondant à l’étirement d’une liaison A - B, notée νAB
- vibration de déformation (ou flexion) correspondant à la variation d’un angle de valence , notée δAB
Ces vibrations peuvent en grande partie s’interpréter dans le cadre de la mécanique classique en faisant appel au modèle simple
de l’oscillateur harmonique. On peut, par exemple modéliser la liaison par un ressort de raideur k dont la fréquence propre de vibration,
donnée par la loi de Hooke, est :
ν = 1
2π k µ
soit
1
λ = 1 2πc k µ
Un tel oscillateur peut également être décrit dans le cadre de la mécanique quantique, son énergie est alors quantifiée et prend
les valeurs E = hν(v + 1/2), v étant le nombre quantique de vibration et ν la fréquence donnée par la loi de Hooke.
2 Couplage des oscillations - Fréquences caractéristiques
a Modes normaux de vibration
On peut modéliser la molécule comme un ensemble d’oscillateurs liés les uns aux autres, donc couplés mécaniquement.
L’ excitation par l’infrarouge d’un des oscillateurs se traduit donc a priori par l’excitation simultanée de tous les oscillateurs, aussi bien
en élongation qu’en déformation. Tous les atomes de la molécule vibrent donc avec une même fréquence ν autour de leur position
d’équilibre. Chacune de ces vibrations d’ensemble de la molécule est appelée mode normal de vibration.
On peut dénombrer les modes normaux de vibration du système :
La molécule possède N atomes, elle a donc 3 N degrés de liberté, 3 correspondent à la translation de la molécule et 3 à sa
rotation autour de son centre d’inertie. Il reste 3 N - 6 degrés de liberté correspondant aux vibrations de la molécule. Il y a donc 3 N -
6 modes de vibrations normaux soit 3 N - 6 fréquences de vibration possibles (au maximum).
Si la molécule est linéaire, 2 angles suffisent à décrire sa rotation. Il y a donc 3 N - 5 modes de vibrations normaux.
Exemple :
H2 O possède 3 modes de vibration :
H
O
H
Elongation asymétrique
3756 cm-1
H
O
H
Elongation symétrique
3652 cm-1
H
O
H
Déformation
1595 cm-1

La molécule d’eau possède donc dans son spectre infrarouge trois absorptions caractéristiques. On remarque, et ces résultats
ont une portée générale :
- les vibrations de déformation ont des fréquences plus faibles que les vibrations d’élongation et correspondent donc à
des énergies inférieures .
( - la vibration asymétrique correspond à une énergie plus importante que la symétrique donc à une fréquence
supérieure )
b Fréquences caractéristiques
Si la situation précédente était générale, la spectroscopie IR ne serait que de peu de secours puisqu’il faudrait connaître la
structure de la molécule pour pouvoir analyser les différents modes de vibration et décrypter le spectre.
Heureusement, le couplage entre les différents oscillateurs ne se manifeste que dans un nombre limité de situations :
- les deux oscillateurs doivent avoir des fréquences propres de résonance aussi proches que possible. En pratique, ceci
n’est réalisé que pour des liaisons identiques ou très semblables.
- les oscillateurs couplés doivent être proches géométriquement. La meilleure situation est celle où les liaisons
couplées sont sur le même atome.
Exemple :
Les liaisons C-C du squelette carboné sont couplées. Les vibrations de la chaîne carbonée sont donc complexes et donnent
naissance à une partie du spectre nommée “empreinte digitale” de la molécule (900-1300 cm
-1
), caractéristique de la molécule mais
difficilement interprétable.
Les liaisons C-H d’un CH3 ou d’un CH2 sont couplées et vibrent simultanément.
Par contre, la plupart des groupes de la chimie organique comportent des liaisons qui peuvent être
excitées presque indépendamment du reste de la molécule (C=O, C-O, O-H, C-N, N-H, etc...). Ces groupes
donneront donc naissance à des fréquences d’absorption caractéristiques ne dépendant que peu de leur
environnement.
La présence dans le spectre d’une absorption à cette fréquence permettra donc d’identifier le groupement et dans certains cas,
l’étude de l’écart entre la fréquence et la valeur typique permettra de préciser l’environnement du groupe.
Exemple :
Une absorption forte entre 1650 et 1800 cm-1 permet d’identifier le groupe carbonyle C=O. La valeur exacte de la fréquence
indique s’il s’agit d’une cétone, d’un aldéhyde, d’un ester, etc...
3 Excitation de la molécule par l’IR - Allure du spectre
a Moment dipolaire de transition
Pour que l’oscillateur mécanique soit excité et entre en vibration, il doit y avoir une interaction avec l’onde électromagnétique
conduisant à un transfert d’énergie. Ceci se produit quand la vibration fait varier le moment dipolaire de la molécule et donc

l’interaction entre le dipôle et le champ électrique de l’onde. L’énergie de vibration étant quantifiée, la transition se produira lorsque
l’on aura h ν = ∆ E, différence d’énergie entre le niveau fondamental et le premier niveau de vibration excité.
La conséquence est que seules les vibrations faisant varier p , le moment dipolaire, sont actives en IR et que l’intensité
absorbée est d’autant plus grande que cette variation est grande.
Les absorptions IR les plus fortes sont donc souvent dues à des groupes très polaires tels C=O, N-O, O-H, etc...
Une double liaison C=C n’est active que si la substitution n’est pas symétrique.
b Allure du spectre
- bandes d’absorption
En phase liquide ou solide, les spectres IR se présentent sous forme d’une suite de bandes d’absorption , avec une allure en
partie semblable à celle des spectres UV /visible. Ceci est du au fait qu’aux transitions de vibration se superposent des transitions de
rotation. L’énergie mise en jeu dans les rotations est beaucoup plus faible et la durée de vie des états de rotation très brève compte tenu
des chocs se produisant dans la phase condensée. A une durée de vie brève est associée une énergie mal définie d’après le principe
d’incertitude d’Heisenberg, l’incertitude sur la valeur de l’énergie devient alors du même ordre de grandeur que l’écart entre niveaux de
rotation (1 cm-1 ). On observe donc une bande, plus ou moins large, centrée sur la fréquence caractéristique de vibration.
Remarque : Ce n’est plus le cas en phase vapeur où les spectres de rotation-vibration sont formées de raies fines.
- autres bandes
Aux 3N-6 fréquences de vibrations normales s’ajoutent sur le spectre d’autres types de bandes :
- les harmoniques (2 ν essentiellement) des bandes les plus intenses . L’harmonique ayant une intensité très faible n’est visible
que si la bande fondamentale est très intense ou si son intensité est renforcée par résonance avec une autre bande.
- les bandes de combinaison ν1 + ν2 résultant de l’excitation simultanée de plusieurs vibrations
L’existence de ces bandes résulte du caractère anharmonique de l’oscillateur, leur intensité reste faible devant celle des bandes
caractéristiques et elles n’ont pas, dans la plupart des cas, à être prises en compte .
4 Influence de divers facteurs sur les fréquences de vibration
On se limite à la discussion de quelques facteurs concernant les bandes d’élongation, pour lesquelles une discussion peut être
menée à partir de la loi de Hooke.
Il est difficile de corréler simplement k aux caractéristiques géométriques et électroniques de la liaison. On ne peut donc que
faire un commentaire qualitatif de certains résultats expérimentaux.
•
Ordre de grandeur de k
Considérons par exemple la fréquence d’élongation de O-H,
1
λ = 3300 cm-1
, l’application numérique de la loi de Hooke
conduit à k = 605 N.m-1 . Les raideurs de liaison sont donc de quelques centaines de N.m
-1
, ce qui est finalement un ordre de grandeur
“macroscopique”.

•
Influence de µ
Pour un même k, l’augmentation de µ déplace logiquement ν vers les basses fréquences. Ainsi, en passant de C-H à C-D, la
fréquence est à peu près divisée par
•
Influence de la multiplicité
k augmente avec la multiplicité. On a donc vC-C < νC=C < νC=
C
et ces fréquences sont très approximativement dans les
rapports 1, ,
•
Influence de la délocalisation
La délocalisation d’une double liaison diminue k et donc abaisse ν. Pour un carbonyle, par exemple, la conjugaison abaisse
νC=Ο d’environ 40 cm
-1.
• Influence des liaisons hydrogène
L’existence d’une liaison hydrogène abaisse la fréquence de la vibration d’élongation O-H . Elle élargit également
considérablement la bande.
(• Influence de la tension stérique)
Lorsque l’oscillateur est lié à une structure tendue stériquement, sa fréquence de résonance est augmentée. Ainsi, la fréquence
de vibration du C=O d’une cétone cyclique augmente quand la taille du cycle diminue.
II Etude des principales bandes de vibration
1 Généralités
Il n’est pas question de faire une analyse exhaustive des spectres mais seulement de reconnaître les principales bandes de
vibration en s’appuyant sur les tables fournies.
Méthode d’étude
On commence d’abord par dépouiller le spectre en partant des hautes fréquences et en notant pour chaque bande semblant
caractéristique trois facteurs importants :
- la fréquence en cm
-1
- l’intensité (tF, F, moyenne, faible) - la largeur (très large à fine)
La valeur de la fréquence n’est pas un critère suffisant pour l’attribution !
On prendra garde à ne noter pour la zone inférieure à 1400 cm
-1
que les bandes ressortant très nettement de l’empreinte
digitale.
La consultation de la table et le croisement des résultats permet à ce stade une attribution probable des bandes et une
identification des groupes correspondants.
On peut ensuite rechercher des renseignements complémentaires dans le reste du spectre et préciser les attributions proposées.