LA CONVERSION DC–DC : LES HACHEURS

M. GARNERO
LA CONVERSION DC–DC :
LES HACHEURS
1° Introduction
2° Hacheur série (Buck)
3° Deux quadrants : Réversible en courant
4° Deux quadrants: Réversible en tension
5° Quatre quadrants
6° Hacheur parallèle (Boost)
7° Hacheur à accumulation inductive (Buck & Boost)
Bibliographie et liens utiles

Page : 2
M. GARNERO 1-Hacheurs
1° - Introduction
Les hacheurs sont les convertisseurs statiques qui
permettent le transfert de l’énergie électrique d’une
source continue vers une autre source continue. (Ils
sont l’équivalents des transformateurs en
alternatif).
Lorsque l’entrée et la sortie sont de natures
dynamiques différentes, on peut les relier
directement (on parle alors de hacheur à liaison
directe). Lorsqu’elles sont de même nature
dynamique, il faut faire appel à un élément de
stockage momentané (on parle dans ce cas de
hacheur à accumulation). Enfin dans le cas où
l’isolation galvanique de la sortie avec l’entrée est
une nécessité, on réalise des hacheurs dits
« isolés ».
Suivant le degré de réversibilité que l’on désire, la
structure du montage diffère.
Enfin, suivant la puissance nominale du système, la
technologie des composants ne sera pas la même.
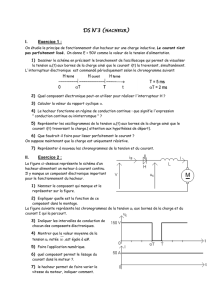
2° - Hacheur série (Buck)
C’est le montage le plus simple et le plus ancien. On
dit qu’il s’agit d’un hacheur à un bras.
Il permet de relier une entrée de type « v » (qui n’a
pas de discontinuité de tension) à une sortie de type
« i » (qui n’a pas de discontinuité de courant). C’est
un hacheur « Un quadrant » qui n’a aucune
réversibilité. L’énergie ne peut circuler que de
l’entrée vers la sortie. Il ne comprend qu’un seul
interrupteur commandé et une diode de roue libre.
Cependant ce transfert est réglable. Le paramètre
de réglage est le rapport cyclique de la commande de
l’interrupteur. Nous allons voir que ce hacheur est
de type abaisseur, la tension de sortie étant
toujours inférieure à la tension d’entrée.
Historiquement, il s’agissait de hacheurs dits « de
traction » qui permettaient de régler la vitesse des
moteurs à courant continu de trains.
L’interrupteur fonctionne périodiquement. La
période de « hachage » est notée T et f la fréquence
correspondante. Il est fermé de t = 0 à t = αT et
ouvert de t = αT à T. (α est le rapport cyclique).
Lorsque l’interrupteur est fermé, l’entrée est
directement reliée à la sortie. Lorsqu’il est ouvert,
entrée et sorties fonctionnent indépendamment.
L’entrée est ouverte, la sortie est en court-circuit
grâce à la diode de roue libre qui assure la continuité
du courant de l’inductance.
On peut faire une analogie avec un cycliste qui
pédalerait de façon saccadée. Pendant une partie du
temps, il pédale (et sa vitesse augmente), ensuite il
se laisse aller sur son élan (grâce à la roue libre du
pignon arrière). Dans cette phase sa vitesse diminue.
On conçoit qu’il y ait deux régimes de
fonctionnement distincts :
- Soit l’élan est suffisant pour atteindre la fin de la
période sans s’arrêter, donc celle-ci se décompose
en deux phases – pédalage, roue libre. La vitesse
croit et décroit mais elle n’est jamais nulle.
- Soit l’élan n’est pas suffisant (à cause d’une côte
ou de frottements trop importants ou par manque
d’inertie) et la période se décompose en trois
phases : pédalage, roue libre, arrêt. Dans ce cas à
chaque période la vitesse initiale est nulle.
Pour le hacheur c’est identique,
soit le courant est suffisant, il est non interrompu tout au
long de la période et elle se décompose en deux phases :
0 < t < αT K fermé, D bloquée, phase active,
αT < t < T Kouvert, D passante, phase de roue libre.
Soit le courant n’est pas suffisant et il s’interrompt avant la
fin de la période qui se décompose en trois phases :
0 < t < αT K fermé, D bloquée, phase active,
αT < t < βT Kouvert, D passante, phase de roue libre,
βT < t < T Kouvert, D bloquée, phase de repos.
Nous allons faire l’étude successive de ces deux régimes
de fonctionnement.
On commencera par le régime DNI (débit non interrompu).
L’exploitation des résultats nous permettra de déterminer
les conditions limites de ce régime, puis nous étudierons le
régime DI (débit interrompu).
L
D
E
1
i
L
v E
2
F,
α
αα
α
v
L
K
i
1
i
D
i
K1

Page : 3
M. GARNERO 1-Hacheurs
a) Débit Non Interrompu dans la bobine
Phase active : 0 < t < αT K fermé
si K fermé, alors v = E
1
> 0, donc D bloquée
Roue libre : αT < t < T K ouvert
si K ouvert mais i
L
≠ 0, alors D passante,
donc v = 0
Calculons la valeur moyenne de v
D
:
V
Dmoy
=
∫
T
dttv
0
)(
T
1
= )E*T(
T
1
1
α = α E
1
La loi des mailles donne par ailleurs :
v = v
L
+ E
2
Si nous calculons à nouveau la moyenne de v
D
, en
considérant que la moyenne d’une somme est la
somme des moyennes et que la moyenne d’une
constante est égale à cette constante alors :
(v)
moy
= (v
L
+ E
2
)
moy
= (v
L
)
moy
+ (E
2
)
moy
V
moy
= (v
L
)
moy
+ E
2
= 0 + E
2
La valeur moyenne de la tension aux bornes d’une
bobine étant toujours nulle en régime périodique
1
, en
identifiant les résultats nous avons :
E
2
= α
αα
α E
1
Comme α est réglable entre 0 et 1, la tension de
sortie devient réglable entre 0 et E
1
.
Le montage est abaisseur de tension.
Déterminons l’allure de v
L
afin de calculer le courant
dans la bobine.
Dans la phase active v
L
= E
1
– E
2
= (1 - α) E
1
C’est une constante positive. Le courant croît
linéairement avec une pente
L
E α )(1
1
−
En notant I
0
la valeur de i
L
à t = 0 le courant sera
régit par :
1
Si on retrouve à chaque période la même valeur de courant, c’est
que «la somme des tensions» pour accroître le courant compense
exactement celle qui l’on fait décroître. Ce qui fait zéro en
moyenne.
Notes personnelles
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
t
v
T
α
T
0 2T
E
v E
2
v
L
E
1
v
E
2
v
L

Page : 4
M. GARNERO 1-Hacheurs
i
L
= I
0
+
L
Eα)(1
1
−
t
A la fin de cette phase il atteint la valeur I
α
I
α
= I
0
+
L
Eα)(1
−
α T
Dans la phase de roue libre v
L
= - E
2
= - α E
1
C’est une constante négative. Le courant décroît
linéairement avec une pente
L
Eα
1
−
A la fin de cette phase il reprend la valeur I
0
Le courant dans la bobine fluctue entre I
0
et I
α
,
l’ondulation de courant vaut donc :
∆I = I
α
- I
0
=
L
Eα)(1
1
−
α T
Elle est nulle lorsque α vaut 0 ou 1 et elle est
maximale lorsque α =0,5 ainsi :
∆I
M
=
L4 TE1
Les chronogrammes des divers courants dans le
montage s’obtiennent simplement (la loi des nœuds
en entrée donnant i
L
= i
1
+ i
D
Plus le courant d’utilisation I
L
est important plus I
α
et I
0
augmentent, par contre l’écart ∆I, entre ces
deux valeurs reste constant.
On peut calculer facilement I
0
et I
α
en notant que
I
Lmoy
= ½ (I
0
+ I
α
) donc
I
0
= I
Lmoy
– ½ ∆I
L
et I
α
= I
Lmoy
+ ½ ∆I
L
Pour terminer ce paragraphe, il faut chercher la
limite de validité de ces équations. Nous sommes
dans le cas de débit non interrompu dans la bobine,
c’est à dire que la valeur minimale I
0
doit être
positive.
Si I
α
et I
0
augmentent lorsque le courant d’utilisation
augmente, ils diminuent lorsque ce dernier diminue.
Le cas limite est obtenu lorsque I
0
= 0 ( et I
α
= ∆I)
Dans ce cas, I
Lmoy
vaut donc ½ ∆I soit donc :
I
lim
=
L2 Eα)(1
−
αT
la plus grande valeur est obtenue lorsque α = 0,5 et
vaut : I
lim max
=
L8 TE
Nous pouvons tracer l’évolution de E
2
en fonction de
I
Lmoy
(courbes paramétrées par α)
b) Débit Interrompu dans la bobine
Phase active : 0 < t < αT K fermé
si K fermé, alors v = E
1
> 0, donc D bloquée
Roue libre : αT < t < βT K ouvert
si K ouvert mais i
L
≠ 0, alors D passante,
donc v = 0
Repos: βT < t < T K ouvert
si K ouvert et i
L
= 0 = cte , alors D bloquée,
et puisque i
L
= cte alors v
L
= 0 et v = E
2
t
v
L
T
α
αα
α
T
0
2T
(1-
α
)E
-
α
E
I
α
I
0
i
L
I
0
t
T
α
αα
α
T
0
I
α
i
1
I
0
t
T
α
αα
α
T
0
I
α
I
0
i
D
t
T
α
αα
α
T
0
I
α
i
L
I
0
t
T
α
αα
α
T
0
I
α
I
0
i
L
I
lim
∆
I
V
S
E
0
DNI
I
Lmoy
DI
α
= 1
α
= 0
α
= 0
,5
α
= 0,25
α
= 0,75
I
lim max
=
L8 TE
t
T
α
αα
α
T
0
2T
E
1
E
2
v
β
ββ
β
T

Page : 5
M. GARNERO 1-Hacheurs
Comme dans le cas précédent calculons les valeurs
moyennes :
V
moy
=
∫
T
dttv
0
)(
T
1
=
( )
1S
E*αTV*βT)-(T
T
1+
V
moy
= V
S
=
(
)
1S
E* α V* β )-(1 + (1)
I
Lmoy
=
∫
T
dtti
0
)(
L
T
1
=
(
)
2
1
'*Iα*βT)
T
1
I
Lmoy
= I
S
=
2
1
*αT*
LE-E
*β21 
(2)
En ordonnant l’équation (1) on obtient :
E
2
=
1
E
β
α
ou encore β =
2
1
E
αE
On peut remarquer que E
2
> αE
1
avec l’équation (2) et l’expression de β, en ordonnant
nous obtenons :
Lmoy
1
2
1
2
I
ETα
L2
1
E
E+ =
Contrairement au cas précédent, E
2
dépend de I
Lmoy
.
Nous pouvons même observer que pour
I
Lmoy
= 0 la tension de sortie vaut E
1
quelle que soit la
valeur de α.
A circuit ouvert, la sortie n’est plus commandée
2
.
On peut compléter les courbes E
2
= f(I
Lmoy
),
ébauchées au paragraphe précédent.
c) Considérations pratiques :
Courant moyen dans la charge
Le modèle précédent ne permet pas de calculer le
courant dans la charge, il faut qu’il soit donné.
2
On peut toujours ajouter au montage une résistance de
« saignée » qui empêche le courant d’être nul.
Notes personnelles
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
t
v
L
T
α
αα
α
T
0
2T
(E-V
S
)
-V
S
I
α’
i
L
β
ββ
β
T
V
S
E
0
DNI
I
S
DI
α
= 1
α
= 0
α
= 0,5
α
= 0,25
α
= 0,75
I
LSM
=
L8 TE