Métrologie et interférences en lumière polarisée - sfo

Optique instrumentale
Métrologie et interférences en lumière polarisée
A.C. Boccara et P. Gleyzes
Laboratoire d Optique Physique, UPR A0005 du CNRS, ESPCI, 10 rue Vauquelin,
75005 Paris, France
Résumé : Le but de cet article est de montrer comment les notions fondamentales décrivant la
polarisation de la lumière peuvent être mises à profit pour concevoir des intruments d'une très grande
sensibilité. Nous insisterons particulièrement sur les effets "d'interférences en lumière polarisée" qui
peuvent être exploités pour meure en évidence des différences de marche de l'ordre du millionième
de la longueur d'onde ce qui reste difficile en interférométrie traditionnelle.
1. POLARISATION : LUMIÈRE ET MATIÈRE
Une description rigoureuse des champs électromagnétiques émis par des ensembles d'atomes
passe par une description statistique des effets physiques rendant compte du rayonnement [1].
Le cas des lasers est parfois plus simple quoique quelques précautions doivent être prises
lorsqu'il s'agit de rendre compte des interactions du champ avec la matière.
Dans cet exposé nous nous limiterons à quelques notions simples qu'il est bon d'avoir à
l'esprit lorsque l'on utilise des montages dont les signaux ont pour origine les effets de
polarisation. Ces notions étant très "classiques" (au sens de l'enseignement de
l'électromagnétisme) il existe des ouvrages en langue française [2] [3] qui couvrent bien la
description "classique" (au sens de la physique quantique) des champs et de leur interaction
macroscopique avec la matière.
1.1 Lumière naturelle et lumière polarisée
1.1.1 Sources incohérentes (spatialement).
Dans ces sources il n'existe pas de corrélations spatiales ou temporelles entre le rayonnement
émis par des atomes différents. De ce fait, même si l'énergie moyenne reçue en un point de
l'espace (r) à partir de la source (placée en O) est parfaitement stable, il y aura de très rapides
fluctuations de la direction du champ électrique de l'onde en r. Les temps caractéristiques sont
typiquement de l'ordre de grandeur de la durée des trains d'ondes (10 8 s pour une source à
basse pression à 10"14 s pour des sources thermiques).
L'observation que nous faisons est généralement "lente" à cette échelle de temps (oeil,
caméra, détecteurs...) ; on pourra rendre compte de l'onde transversale émise par la source
Article disponible sur le site EDP Sciences et disponible sur le site http://sfo.edpsciences.org
ou http://dx.doi.org/10.1051/sfo/1997015

92 A.C. Boccara et P. Gleyzes
-*->-»
par la superposition de deux champs ( E = E|+ E2) orthogonaux dont nous mesurons la
valeur moyenne du carré du module (valeur moyenne prise sur le temps de réponse du
détecteur).
Il faut souligner : —» —»
- Le choix arbitraire de la base : (par exemple Ei et E2 peuvent être choisis selon
i et j i -L j ou selon ai + ß j et ß i - a j Va,p pour des polarisations
linéaires). —» —»
- Le choix arbitraire des deux états de polarisation représentant Ei et E2 (linéaire,
circulaire, elliptique).
- La mesure, dans le domaine optique, n'est pas celle du champ, mais les détecteurs
(quadratiques) fournissent un signal proportionnel à la puissance reçue intégrée sur le temps
de réponse du système de mesure.
Nous appellerons polariseur un système capable d'imposer une différence de phase, ô,
constante au cours du temps entre les deux états de polarisation qui nous ont servi de base.
Exemples Base cartésienne ( i > j )•
Polarisation linéaire : ô = 0 modulo n.
E = Ej + E2 reste parallèle à une direction fixe au cours de la
propagation de l'onde.
Polarisation circulaire : ô = ± ^ modulo 2n et a = ß.
Polarisation elliptique : ô = constante.
Si nous imposons les axes x et y, un polariseur linéaire P imposera la mise en phase ô
des deux composantes (de la lumière naturelle). La direction de la polarisation émergente
étant fixée par le rapport des amplitudes selon x et y. Remarquons que quelle que soit la
direction de polarisation recherchée l'énergie recueillie sera proportionnelle à <E2>
= < (a cosG + ß sinG)2 > où G est l'angle ( i, P).
Comme < aß cos G sin G >= 0 on trouve < E2 > = ~(E2 + c'est-à-dire la moitié de
l'énergie incidente.
1.1.2 Sources cohérentes (Lasers).
Très souvent on a tendance à confondre les effets de cohérence et de polarisation dans le cas
des lasers. Remarquons d'abord que si de nombreux lasers fournissent une lumière
(fortement) polarisée, c'est dû à des effets d'anisotropie du milieu amplificateur (gain du
matériau cristallin pour une direction particulière du champ) ou de la structure (fenêtres, ou
milieu amplificateur sous l'incidence de Brewster qui favorise une polarisation comme on le
verra plus loin).
Lorsque la symétrie est telle que le système est isotrope perpendiculairement à sa
direction de propagation, rien ne devrait favoriser des directions particulières du champ
électrique. En fait, pour des raisons technologiques (défauts) ou physiques (effet Zeeman), on
observe à la sortie de tels lasers (HeNe) deux polarisations orthogonales stables au cours du
temps. Ces deux états de polarisation (linéaires, ou circulaires dans le cas du laser "Zeeman")
correspondent à des modes différents qui n'ont pas de relations de phase bien définies mais

Métrologie et interférences en lumière polarisée 93
qui, compte tenu de la "longueur des trains d'ondes" (cohérence), peuvent "battre" à des
fréquences allant de quelques MHz (Zeeman) au GHz.
1.2 La polarisation et les milieux matériels
Nous n'avons, jusqu'à présent, décrit les effets de polarisation que de façon
phénoménologique sans indiquer ce qui pouvait créer, transformer ou détruire un état de
polarisation.
Ces effets sont obtenus, par l'interaction de la lumière et de la matière, de très
nombreuses façons : réfraction, diffusion, absorption, émission... Nous nous limiterons ici à
la description "macroscopique" de ces interactions dans deux cas très classiques : les effets
d'interfaces (réflexion, transmission) et les milieux anisotropes (propagation).
Rappelons nous simplement que le comportement des ondes électromagnétiques dans un
milieu matériel (linéaire et homogène) ressemble à celui qu'elles ont dans le vide (surtout
pour les milieux transparents) mais qu'il faut tenir compte de la polarisabilité du milieu qui
intervient par sa constante diélectrique (e = £0£r) ou par son indice de réfraction er = n2e
er et n sont des grandeurs réelles positives dans le cas des milieux transparents (c'est à dire
lorsque la fréquence de l'onde est plus basse que celles des résonances électroniques) et
négatives ou complexes dans le cas contraire.
1.2.1 Réflexion et transmission à l'interface entre deux milieux isotropes.
Les relations entre les champs incidents et les champs réfléchis ou transmis s'obtiennent en
écrivant la continuité des composantes tangentielles des champs (électriques et magnétiques)
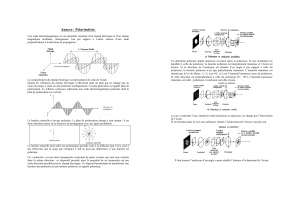
à l'interface. Par exemple si nous cherchons à exprimer les facteurs de réflexion rp et de
transmission tp pour la polarisation linéaire parallèle au plan d'incidence (figure 1), la
continuité des composantes tangentielles du champ conduit à :
E. cos i, + E„ cos i, = E_ cos L
îp l rp 1 tp 2
E rp . tp
si r = —— t = —- on aura :
P E. P E.
ip ip
(l + rp)cosi, = tp cosi2 (1)
Pour cette même polarisation, compte tenu de la continuité du champ magnétique qui est
perpendiculaire au plan d'incidence, on trouve : n](l - rp) = n2tp (2) et en combinant (1) et
(2)
n, /cos i. - n„ / cosL
r =-î i 2 2. (3)
P nt /cosij +n2 /cosi2
On montrerait de même que pour la polarisation (s) perpendiculaire au plan d'incidence
t
P "2 ' " ' (4)

94 A.C. Boccara et P. Gleyzes
_ i^cosi, -n2cosi2
' rijCosi, + rijCosij
t.=l + r, (6)
Figure 1 : Calcul des facteurs de réflexion rp ei de transmission tp à l'interface entre deux milieux d'indices ni
etn2-
Ces formules sont très faciles à utiliser, elles permettent de calculer le comportement de
systèmes simples (un seul matériau) ou complexes (succession de couches minces) en tenant
compte de la loi de la réfraction (ni sin ii = n2 sin i2) et des effets d'interférences éventuels.
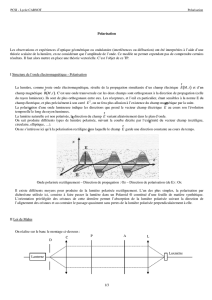
A titre d'exemple la figure 2 représente les facteurs de réflexion air-eau, air-verre, air-
germanium (dans l'infrarouge) en fonction de l'angle d'incidence.
L'utilisation des formules ci-dessus et l'observation des courbes appellent quelques
commentaires :
- Les états "propres" de la polarisation (ceux qui sont conservés par réflexion ou
transmission) correspondent aux polarisations linéaires parallèle ou perpendiculaire au plan
d'incidence. Si on s'intéresse au devenir d'un état de polarisation incident quelconque, il
faudra décomposer le champ correspondant sur cette base (p,s) puis le recomposer après
interaction avec la surface (cf. ellipsométrie dans les exemples ci-dessous).
- Les formules rendent compte des amplitudes des champs, aussi faut-il prendre le
carré du module pour la réflexion Rp s et faire attention aux quantités pertinentes (densité
d'énergie ou flux total) pour la réfraction (le plus simple est de calculer TpS=l - Rp,s).
- Ces formules sont applicables avec des valeurs complexes de l'indice, il faut
simplement remarquer que lorsque l'incidence est oblique les ondes réfractées (par exemple à
l'interface entre un milieu transparent et un milieu absorbant) ne sont plus homogènes (les
plans équiphases ne sont plus des plans équiamplitudes).

Métrologie et interférences en lumière polarisée 95
- Au delà de l'angle limite ces formules restent valables pour les champs évanescents
(qui sont aussi des ondes non homogènes).
AS-
AI -
0l7 •
M -
AS -
0.4 -
0.3 -
os-
ai -
0 10 20 30 -40 50
70 80 90
Figure 2 : Facteurs de réflexion (intensité) à l'interface air verre Rp ( ) et Rs (—) dans le visible et air
germanium dans l'infrarouge Rp ( ) et Rs ( ).
1.3 Application : principe de l'elltpsométrie
Ces quelques notions sur les effets de polarisation aux interfaces vont nous servir à montrer
combien la lumière constitue une sonde sensible de ces interfaces et comment de très faibles
perturbations très inférieures à la longueur d'onde peuvent être révélées par analyse de l'état
de polarisation réfléchi ou transmis.
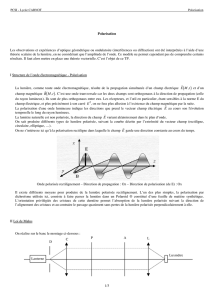
Bien que le schéma proposé ne soit pas le seul possible, la figure 3 nous fournit le
principe d'une mesure ellipsométrique : une lumière incidente polarisée à 45 0 du plan
d'incidence se divise en deux composantes d'égale amplitude Epi et Egi respectivement
parallèle et perpendiculaire au plan d'incidence. Chacune de ces composantes sera réfléchie
par l'échantillon avec les facteurs complexes rp et rg. Le rapport des modules tgy de ces
facteurs complexes fixe la direction du grand axe de l'ellipse représentant le champ réfléchi,
la différence des arguments (A) fixe l'ellipticité (rapport des axes).
échantillon
Figure 3 : Principe de l'ellipsométrie.