DYNAMIQUE DUVEHICULE - Cahier 2 - Interaction véhicule

LANIERE EXPERIMENTALE
2" année fcycle
I JR BROSSARD |
wmmmm
CAHIER 2
Interaction véhicule-sol
Voir aussi cahier 1.3 Mécanique ; JR BROSSARD
Voir aussi cahier 4 Construction = G. PANEL
© [JP. Brossard],[1980], INSA de Lyon, tous droits réservés

1
INTERACTION SOL-VEHICULE
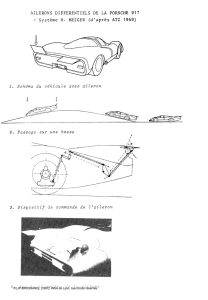
I - ANALYSE DU COMPORTEMENT D'UNE ROUE ISOLEE AVANÇANT A VITESSE
UNIFORME
Schéma d'expérience
B, XÎ, YÎ, Z"!" repère en translation
par rapport à (0, X . Y . Z„) lié
au sol.
Les actions appliquées à la roue peuvent êtrç représentées
par le torseur T^ (torsei^r des forces ?!donnêesff)
Fj = [XD, Yp> ZD]^
M^ (B) = [LDf Mp, ND]
Les actions de contact sol-roue peuvent être représentées
par le torseur.
F0R =
LX0R'
Y0R' Z0R-'1
M^(A) - [LQR, M0R, N^
© [JP. Brossard],[1980], INSA de Lyon, tous droits réservés

Sur la roue agissent également les actions de pesanteur
représentées par le vecteur
? = - Mg ZT^ e?n B
En outre on supposera que la liaison de la roue /(So) est
parfaite.
Lorsque la roue roule sans glisser sur le sol (VR°(A) = 0)
on a :
I xf - a *' = 0
MXOR1 < f IV
jîM0RI = h |Z0RI
\ M0R de signe opposé à <f>
f
h est le paramètre de résistance au roulement x h est de l!ordre de
-3
10 m* En fait on nfutilise pas le paramètre de résistance au roulement
mais une autre formulation.
11 - COEFFICIENT DE FROTTEMENT DE ROULEMENT
Dans tout ce qui suit on supposera xf > 0 x! = cte
Appliquons les théorème^ généraux à la roue seule
XD + X0R " °
ZD + ZQR - mg = 0
MD + $A A ?OR) f1 + M0R = °
Les lois de COULOMB donnent :
MOR
= -hZOR (ZOR>0 *'>C))
Le théorème du moment s?écrit donc :
MD " R XOR - h ZOR = °
y - D _ A 7
OR ~ R" R AOR
Pour une roue soumise a aucun couple M~ = 0
© [JP. Brossard],[1980], INSA de Lyon, tous droits réservés

Y = . h 7
OR R OR
Y = îl 7
AD R OR
X^ est la force de traction nécessaire pour faire avancer la roue.
Sa connaissance permet donc de connaître la résistance au roulement.
REMARQUE : La formule X0R e " D ^QT) est tout à fait analogue à la
formule de COULOMB s'il y avait glissement
Y - _ f y
OR * OR
— est sans dimension. On posera :
K
h _
R " »
•\x est appelé coefficient de frottement de roulement et
cfest lui que lfon utilise pour caractériser la résistance
au roulement,
10 -2
p est de lford:e de ~*?r~r ~ 2,10 mais nous étudierons plus
en détail sa variation notamment en fonction de la vitesse
et de la pression*
III - RESULTATS GLOBAUX SUR LE VEHICULE
© [JP. Brossard],[1980], INSA de Lyon, tous droits réservés

Lféquation 3 s!êcrit donc compte tenu de (1) et des loi3
de Coulomb
- 2 a1 Z 1 + 2 a9 Z _ - C (£ Cx SV2 - X) - 2h Zn1 - 2h Z 7
1 ol l o3 v2 °* °3
+ E cM i gv2 =; o
a M
Or h <<a. et h <<a?
A lfavant par raison de symétrie
X01 = X02 " ~ R Z01 M01 = " h Z01
[Z01 = Z02 M02 = " h Z02
A lf^.rrière
X03 X04 = " R Z03 M03 ^ - h ZQ3
Z03 = Z04 M04 ~ " h Z04
Supposons le véhicule avançant en ligne droite à vitesse
constante, remorqué par un autre véhicule « Le véhicule tracteur exerce
des actions représentées par le torseur
% = [X, 0, 0]1 MD(G) - [0, 0, 6}
Les théorèmes généraux appliqués au véhicule donnent
© [JP. Brossard],[1980], INSA de Lyon, tous droits réservés