Cours Peception Auditive

1
Université Montpellier 2
Licence Professionnelle Acoustique
Perception Auditive
F. GENIET
Septembre 2009

2
I. La nature du phénomène sonore
1) La chaîne de l’audition.
La vue très schématique ci-dessus permet de préciser les domaines mis en jeu dans la chaîne
de l’audition :
Les deux premiers blocs font partie de la physique : mécanique et acoustique permettent
en principe d’expliquer la génération et la propagation des sons. Rappelons que le son dans
l’air est une onde de compression mécanique longitudinale, dont la propagation est décrite par
l’équation d’onde (ou équation de d’Alembert)
0
1
2
2
2
=∆−
∂
∂p
t
p
c
la grandeur p(x,y,z,t) représente la surpression régnant au point (x,y,z) à l’instant t, et c
représente la célérité de l’onde sonore
M
RT
c
γ
=
γ =5/3 pour un gaz diatomique, R = 8.32 J mol
-1
K
-1
est la constante des gaz parfaits, et M est
la masse molaire du (mélange de) gaz. Dans le cas de l’air M ≈ 29 10
-3
kg, et c ≈ 331 ms
-1
à
0°C .
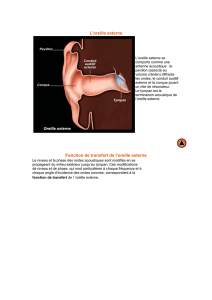
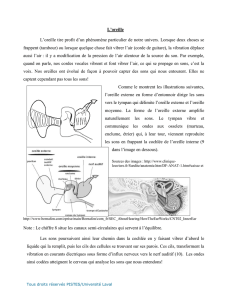
La description du mécanisme de fonctionnement de l’oreille, bien qu’en très grande partie
faisant appel à l’acoustique, fait partie du domaine de la physiologie. Ce fonctionnement est à
peu près bien connu depuis le siècle dernier (XXème) bien que les recherche sur le sujet se
poursuivent (Cf. cours G. Rebillard), et que tout le monde ne soit pas tout à fait d’accord sur
tous les mécanismes.
Le système de transducteur au niveau de l’oreille interne, transformant la vibration
mécanique en influx nerveux et potentiel d’action, fait partie du domaine de la
neurophysiologie, domaine ayant énormément progressé depuis 50 ans, grâce en particulier
aux micro électrodes permettant de capter l’influx nerveux in vivo au niveau d’une seule
cellule (Cf. également cours G. Rebillard).
Source
Sonore
Propagation
Réception
Oreille
Sensation
Interprétation

3
Enfin, et c’est une partie qui va nous intéresser en particulier, la question de savoir
comment nous percevons les sons, et comment nous les interprétons, bien qu’en principe
réductible à la neurophysiologie (ce qui est totalement inenvisageable à l’heure qu’il est), fait
appel au domaine de la psychophysique, ici la psycho-acoustique, qui tente de corréler des
excitations physiques à nos sensations psychologiques. Dans ce domaine, le sujet percevant
est évidemment un personnage clé (ce que n’aiment pas les physiciens !) et les expériences
doivent être répétées de façon à obtenir des résultats statistiquement valables.
Dans ce dernier domaine, la grande question est :
« peut on relier ce que l’on mesure physiquement (fréquence, puissance, composantes
de Fourier, sonagramme…) à ce que l’on perçoit, (sont aigu, intense, agréable…) ? »
qui va en grande partie nous intéresser ici. Notez que la réponse à cette question dépend
beaucoup de la profession de la personne à qui elle est posée :
- pour un musicien, c’est impossible, et de fait, la subtilité des phénomènes
acoustiques musicaux, et des sensations qui y sont reliées sont telles que l’on ne sait
pas les relier par des lois simples.
- Cependant pour un physicien ou un spécialiste d’acoustique industrielle, il semble
par exemple y avoir une corrélation très claire entre l’exposition à un bruit intense
et de façon prolongée (chose que l’on peut mesurer), et l’apparition de surdité à
telle ou telle fréquence. La correspondance n’est pas très subtile, mais elle est
néanmoins très utile. C’est ce point de vue que nous adopterons dans ce cours.
2) Les caractéristiques de la vibration sonore.
a) Observation du signal sonore brut.
Un microphone permet de capter la surpression (on la vitesse) de l’air en un point, et
l’enregistrement, maintenant numérique, permet de visualiser très facilement le signal :

4
En premier lieu, on remarque que l’on est totalement incapable de dire à quoi correspond cet
enregistrement, sauf qu’il est porteur d’information (ce n’est pas un bruit au sens ou on
l’entends en traitement du signal), et que c’est sans doute de la musique (une sorte de
régularité apparaît). Si on veut relier mesures et interprétation, il va falloir travailler !
On remarque alors de façon frappante des « structures temporelles emboîtées », qui
apparaissent au fur et à mesure que l’on zoome.
A la fin, on obtient un signal de forme assez variée selon que c’est une voix, un instrument ou
un autre, l’environnement. Ce signal de pression est plus ou moins périodique, et on ne le
comprend pas plus que le précédent (notez l’échelle temporelle) :
En résumé, on voit se dégager les échelles temporelles suivantes :
b) Fréquences et hauteurs.
Les physiciens et acousticiens et spécialiste du traitement du signal utilisent ici le concept de
« son pur », c'est-à-dire un son dont l’amplitude variant de façon sinusoïdale au cours du
temps. Nous verrons pourquoi c’est très commode pour le traitement du signal (filtrage). Du
point de vue psychoacoustique, c’est un très mauvais choix, et une des raisons de la méfiance
des musiciens à l’égard des acousticiens en découle : les sons purs sont totalement non
musicaux (par exemple la ronflette 50Hz due au secteur est un son pur !) . Pour de tels sons
purs, la fréquence f du signal est reliée à la période par f = 1/T , et donne le nombre
d’oscillations en une seconde.
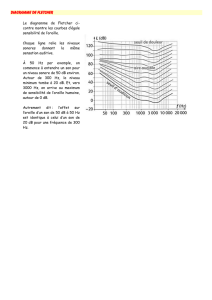
On peut alors vérifier expérimentalement que l’oreille humaine est sensibles aux sons de
fréquences comprises entre environ 20 Hz et 20000 Hz. Cet intervalle se modifie avec l’age
en se réduisant dans les hautes fréquences (cf. Chapitre III). Au-delà, ce sont les ultra sons,
auxquels sont sensibles les chiens par exemple. En deçà, les infrasons que perçoivent par
exemple les éléphants.
10
-
4
s 10
-
3
s 10
-
2
s 10
-
1
s 1 s 10 s 10
2
s
durée des œuvres
10
3
s
durée des notes
et des mots
sensation de
hauteur
percussions

5
On remarque alors que la fréquence f la plus basse du signal, dite fondamentale
1
, est associé
à la hauteur perçue. Pour un diapason, par exemple à 440 Hz, dont les oscillations produisent
une vibration quasi sinusoïdale, la fréquence est relié à la sensation La
4
pour toute oreille de
musicien entraîné.
Si on double la fréquence f = 880 Hz, le musicien perçoit une note située un octave au dessus
(essayer avec un piano) et ainsi de suite. Une progression géométrique (2,4,8,16…) de notes,
correspond ainsi (en très bonne approximation) à une progression arithmétique (0,1,2,3…) de
hauteurs :
Fréquence(Hz) 27,5 55 110 220 440 880 1760 3520 4186
note La
-1
La
0
La
1
La
2
La
3
La
4
La
5
La
6
Do
7
note la
plus
basse du
piano
3
ème
corde
contre
basse
5
ème
corde
guitare
2
ème
corde
violon
Si
4
note
la plus
aigue de
la guitare
Si
5
note
la plus
aigue du
violon
note la
plus
aigue du
piano
Les fréquences supérieures (de 5000 à 20000 Hz) ayant un rôle essentiel dans la perception du
timbre de la voix et des instruments, et des transitoires (attaques, percussions, consonnes).
De ce qui précède, on voit qu’il est naturel d’introduire une échelle logarithmique de hauteur :
c’est notre premier exemple de la loi de Fechner : « la sensation varie comme le log de
l’excitation ». On définit donc l’échelle d’intervalle entre deux fréquences f
1
et f
2
dans
l’échelle des Savarts par
)(log
1
2
10
1000 f
f
I
S
= ce qui donne 1 Octave ≈ 300 Savarts (301,03), et 1/2 ton ≈ 25 Savarts.
De même l’échelle des Cents, plus précise, et plus simple
)(log
1
2
2
1200 f
f
I
C
= ce qui donne 1 Octave = 1200 Cents, et 1/2 ton = 100 Cents.
1
en première approximation et de façon grossière. La sensation de hauteur est en fait bien plus subtile, en
particulier pour les sons musicaux. Nous y reviendrons plus tard.