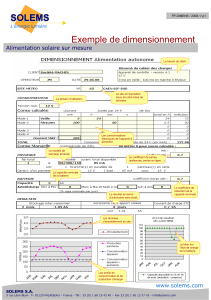
Etude d`un véhicule élec

TS SI
1
Etude d’un véhicule électrique
Sa masse M est de 1400kg
Sa vitesse maximale Vmax=150km/h
Autonomie de 250km à 90km/h
Batterie Lithium-ion
Les deux roues avant sont motrices
Le diamètre D d’un pneu sous pleine charge est de 70cm.
La chaîne cinématique de la propulsion est tracée ci-contre.
Le rendement de la transmission (réducteur et différentiel) vaut η
t
=0,92
Le rapport de réduction
Ω
Ω
== r
N
Nr
kr
est de 0,23
1-Les forces résistances au mouvement du véhicule
1.1) La force nécessaire à la pénétration dans l’air Fa
Elle se calcule par application de la relation :

TS SI
2
Ρ est la densité du véhicule ; ρ=1,3kg/m
3
S est la surface « prise au vent » ; S=1,2m
2
Cx est le coefficient de pénétration dans l’air ; Cx=0,29
V est la vitesse du véhicule en m/s
Calculer cette force pour la vitesse de 90km/h.
1.2) La force de résistance au roulement Fro
Elle se calcule par application de la relation
Fro=Mxgx(12,5x10
-3
+32,4x10
-6
xV
2
)
V est la vitesse du véhicule en m/s
M est la masse du véhicule
g est l’accélération de la pesanteur ; g=9,81m/s
2
Calculer cette force pour la vitesse de 90km/h.
1.3) La force à vaincre sur terrain en pente Fp
Elle est due à la partie du poids du véhicule qui travaille dans la pente.
La pente est de 8%. Le véhicule s’élève de 8m lorsqu’il a parcouru 100m.

TS SI
3
Pour une masse du véhicule égale à 1400kg et g=9,81m/s
2
. Montrez que la valeur de Fp est de
1095N.
2-La puissance, le couple et la vitesse de rotation du moteur
On considère trois situations typiques d’utilisation du véhicule.
2.1) Déplacement sur terrain plat à une vitesse de 90km/h
Les forces résistantes sont Fa et Fro.
Calculer la puissance Pv1 nécessaire au déplacement.
Tenir compte du rendement de la transmission pour montrer que la puissance P1 fournie par le
moteur est égale à 16kW.
Calculer la vitesse Ωr1 de rotation des roues.
Tenir compte du rapport de réduction pour montrer que la vitesse Ω1 de rotation du moteur est
égale à 311 rd/s.
Quelle est la valeur T1 du moment du couple développé par le moteur ?
2.2²) Déplacement sur une rampe de 8% à une vitesse de 90 km/h
Les forces résistantes sont Fa, Fro et Fp
Calculer la puissance Pv2 nécessaire au déplacement.
Tenir compte du rendement de la transmission pour montrer que la puissance P2 fournie par le
moteur est égale à 45,8 kW.
Quelle est la valeur T2 du moment du couple développé par le moteur ?
2.3) Démarrage de la voiture
2.3.1) Calcul préalable du moment d’inertie ramené à l’arbre du moteur.
Evaluer l’énergie cinétique Wc accumulée dans la voiture à la vitesse de 90 km/h

TS SI
4
Cette énergie à été fournie par le moteur en rotation.
Evaluer l’énergie cinétique Wcm fournie par le moteur en tenant compte du rendement de la
transmission. On rappelle que Wcm=1/2xJxΩ
2
Montrer que le moment d’inertie est J=9,83kg.m
2
.
La voiture démarre sur terrain plat et passe de 0 à 50 km/h en 12,2s.
Le moment du couple résistant Tres reste constant égal à 51,4Nm.
2.3.2) Calcul de l’accélération angulaire (dΩ/dt) du moteur lors du démarrage.
Evaluer la vitesse du moteur lorsque la voiture roule à 50 km/h.
Tracer sur la copie la courbe Ω=f(t) lors du démarrage
En déduire l’accélération angulaire du moteur.
2.3.3) Calcul du moment T3 du couple du moteur lors du démarrage.
Rappeler la relation qui lie J, (dΩ/dt), Tmot et Tres lors d’un mouvement de rotation.
Utiliser cette relation pour montrer que T3=190 Nm.
Quelle puissance maximale Pmax est fournie par le moteur au cours du démarrage ?
3- Choix du moteur
On donne sur le document réponse n°1 les caractéristiques mécaniques maximales de deux moteurs.
Placer sur le graphique les trois points de fonctionnement précédent (plat, pente et démarrage).
Lequel des deux moteurs permet le fonctionnement désiré de l’automobile ?
4-Dimensionnement de la source d’énergie embarquée
L’autonomie de la voiture est de 250 km à 90 km/h sur terrain plat.
La puissance fournie par le moteur est alors de 16 kW.
Le rendement du moteur est de η=0,80.
Calculer la durée tu d’utilisation possible du véhicule.
En déduire que l’énergie embarquée doit être égale à We=55,6 kWh.
On suppose la voiture équipée d’un moteur à combustion alimenté en super carburant (SP98).
L’énergie massique du super carburant est de 12,33 kWh/kg.
Quelle masse Ms de super carburant faut-il utiliser pour répondre au besoin d’autonomie du
véhicule ?

TS SI
5
On suppose la voiture équipée d’un moteur électrique alimenté par une pile à hydrogène. L’énergie
massique de l’hydrogène est de 40 kWh/kg.
Quelle masse Mh d’hydrogène faut-il pour répondre au besoin d’autonomie du véhicule ?
Le véhicule est, en fait, équipé d’un moteur électrique alimenté par une batterie d’accumulateurs
Lithium-ion.
Donner, à l’aide des informations du tableau, les arguments qui ont fait choisir le type
d’accumulateur.
Battery Type W*Hr/Litre Watts*Hr/kg Life(re-charge) US$/Watts
Plomb 65 35 400 $0.16
Nickel-cadmium 150 60 500 $0.96
Lithium ion 330 720 1100 $0.16
Déduire de la puissance absorbée par le moteur et de l’énergie embarquée la masse Mb et le volume
Vb de la batterie.
La batterie d’accumulateurs doit délivrer son énergie sous une tension Ub=216V. Elle est constituée
de cellules comprenant 6 éléments de 3,6V connectés comme précisé ci-dessous.
Quel nombre de cellules doit-on monter en série pour obtenir la tension Ub désirée pour la batterie ?
La capacité d’un élément Ce s’exprime en A.h. Elle vaut 43 A.h. L’énergie stockée dans un élément
(en Wh), se calcule par We=3,6Vx43A.h soit 154,8 W.h.
Quel est le nombre N d’éléments nécessaires au stockage des 55 600 Wh embarqués ?
En déduire le nombre Nc de cellules utilisées.
Quel est le montage des cellules ?