Un Univers en mouvement - Le Repaire des Sciences

Seconde – Sciences Physiques et Chimiques Cours
1ère Partie : L’Univers – Chapitre 4
Un Univers en mouvement
1 – Décrire un mouvement
1.1 – Centre d’inertie d’un système mécanique
Le point d’un système dont le mouvement est le plus simple est appelé centre d’inertie du système ; il
est souvent confondu avec son centre de gravité (barycentre des masses).
Avant toute étude mécanique, le système étudié doit être clairement défini et son centre d’inertie
identifié ; ce point servira, par exemple, pour modéliser les actions mécaniques à l’aide de vecteurs
forces.
1.2 – Trajectoire et vitesse caractérisent le mouvement dans un référentiel
L’étude mécanique d’un système ne peut se faire qu’une fois le référentiel d’étude posé. Ce
référentiel, choisi par le physicien, est un solide de référence considéré immobile à partir duquel on
décrira le mouvement à étudier.
A titre d’exemple,
Un référentiel terrestre a pour point de référence un point à la
surface de la Terre ; c’est un référentiel de choix au laboratoire
pour étudier le mouvement des objets qui nous entourent en
classe.
Un référentiel géocentrique a pour origine le centre de la Terre ;
il est particulièrement adapté à l’étude du mouvement des
satellites terrestres comme la Lune.

Seconde – Sciences Physiques et Chimiques Cours
1ère Partie : L’Univers – Chapitre 4
Un référentiel héliocentrique (ou de Kepler) a pour origine le
centre du Soleil ; il est particulièrement adapté à l’étude du
mouvement des objets dans le Système solaire.
La description d’un mouvement nécessite celle de la trajectoire et de la vitesse instantanée du
système.
La trajectoire d’un point est l’ensemble des positions occupée par ce point au cours du mouvement.
Cette trajectoire peut être rectiligne ou curviligne (circulaire, elliptique, parabolique, etc.).
La vitesse instantanée est celle du système en toute position au cours du mouvement : dans une
voiture, c’est celle donnée par le compteur de vitesse.
Le mouvement peut être uniforme (vitesse constante) ou varié (accéléré ou ralenti).
Ainsi, un mouvement rectiligne et uniforme est parfaitement décrit par ces deux termes : rectiligne
(trajectoire « droite ») et uniforme (vitesse constante).
Le mouvement de la Lune autour de la Terre est circulaire (translation circulaire) et uniforme.
La chronophotographie est un outil privilégié pour l’étude d’un mouvement : il s’agit de la
superposition de photographies du mouvement prises à intervalle de temps régulier. Les clichés de
caméra permettent d’obtenir facilement des chronophotographies : la caméra prend des photos plus
vite que le dixième de seconde, qui est la limite de persistance rétinienne de l’œil (l’œil ne peut pas
distinguer des images qui se succèdent plus vite, le principe de la caméra repose sur ce « défaut »).
En 1878, le britannique Muybridge a l’idée de disposer
plusieurs appareils photo sur le chemin emprunté par un
cheval au galop, avec une question : le cheval a-t-il a tout
instant un sabot au sol ?
En 1882, le français Marey invente le fusil photographique où
une plaque circulaire portant des plaques photo tourne à
chaque prise de vue. La caméra était née !

Seconde – Sciences Physiques et Chimiques Cours
1ère Partie : L’Univers – Chapitre 4
Trajectoire et vitesse – c’est-à-dire mouvement – dépendent du
référentiel d’étude. Ainsi, on a longtemps utilisé des courbes complexes
(combinaison d’épicycles et de déférents) pour expliquer le mouvement
apparent des planètes (étymologiquement, la planète est un astre
errant) dans le ciel. Ci-contre, une rétrogradation de la planète Mars.
Copernic et Kepler cherchèrent des moyens plus simples (et tout autant révolutionnaires) pour
expliquer l’observation, mettant à mal le géocentrisme ; Galilée invoqua le Rasoir d’Ockham (ou
principe d’économie) en postulant que, si la Terre et les planètes tournent autour du Soleil, tout
s’explique simplement !
2 – L’interaction gravitationnelle
2.1 – Interaction entre deux corps
La Terre exerce une action mécanique attractive sur tous les corps ou objets, action responsable de
leur chute. Il en est ainsi de l’attraction de la Terre sur la pomme qui, en tombant, aurait bien inspiré
Isaac Newton (1642-1727).
Ce fait est général et réciproque : deux objets, quels qu’ils soient, exercent l’un sur l’autre une action
mécanique attractive ; on dit qu’ils sont en interaction gravitationnelle.
Epicycles et déférents, inventés par Hipparque
et sophistiqués par Ptolémée (IIème s. av. J.-C.)
La Terre et Mars tournent autour du Soleil : la
rétrogradation de la planète rouge s’explique !

Seconde – Sciences Physiques et Chimiques Cours
1ère Partie : L’Univers – Chapitre 4
2.2 – La loi de la gravitation universelle
Dans ses Philosophiae Naturalis Principia Mathematica, Newton précise comment la masse des objets
intervient dans leur interaction et pourquoi leur attraction diminue à mesure qu’ils s’éloignent l’un
de l’autre.
Deux objets A et B, de masses respectives mA et mB, dont les centres de gravité sont séparés par une
distance d, exercent l’un sur l’autre des actions mécaniques que l’on modélise par des forces
attractives de même intensité,
/ / 2
A B
A B B A
m m
F F G
d
où les masses sont en kilogrammes (kg) et la distance en mètres (m) ; G est la constante de gravitation
universelle
G = 6,67.10–11 N.m2.kg–2
En toute rigueur, cette loi n’est valable que pour des objets dont la masse est répartie régulièrement
et de façon sphérique (répartition sphérique de masse), à l’image d’une boule bien homogène.
Application
1. Calculer l’intensité de la force d’attraction gravitationnelle exercée par la Terre sur la Lune,
puis de celle exercée par la Lune sur la Terre.
Données : MT = 6.1024 kg ; ML = 7.1022 kg ; dTL = 400 000 km
Réponse : FT/L = FL/T = 2.1020 N
2. Calculer l’intensité de la force de gravitation exercée par un élève de 50 kg sur un autre élève
de 50 kg situé à 1 m de lui. Conclure.
Réponse : F = 2.10–7 N, cette intensité est 1027 fois moins intense que celle qui retient la Lune
près de la Terre !!
3 – Poids et attraction gravitationnelle
3.1 – Poids et chute des objets
Deux objets lâchés simultanément de la même hauteur touchent
le sol au même instant. Ce résultat surprenant n’est vrai que si
la résistance de l’air agissant sur ces corps est négligeable.
Galilée (1564-1642) fut le premier à montrer que tous les corps
chutent à la même vitesse et ce indépendamment de leur masse.
Aussi l’attraction terrestre s’exerce-t-elle sur n’importe quel
corps avec la même « capacité d’attraction ».
L’importance de cette « capacité d’attraction » est appelée intensité de pesanteur.
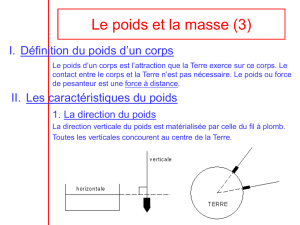
Le poids d’un objet est la force qui traduit la manifestation de la gravitation au voisinage de la Terre ;
cette force est verticale (fil à plomb) et dirigée vers le sol.
René Magritte,
Le grand style
(1951).
En 1971, Dave Scott profite de la
mission Apollo 15 pour vérifier les dires
de Galilée… sur la Lune !

Seconde – Sciences Physiques et Chimiques Cours
1ère Partie : L’Univers – Chapitre 4
Attention : il ne faut pas confondre poids et masse ! La masse est une grandeur traduisant combien
l’objet est massif, c’est-à-dire de quelle quantité de matière (matière ~ massif : même racine) il est
fait : elle est indépendante de l’endroit de l’espace où se situe l’objet, ce qui n’est pas le cas du poids.
En un lieu donné, l’intensité P du poids et la masse m
d’un objet sont proportionnelles,
P m g
où le poids est donné en newtons (N) si la masse est
en kilogrammes (kg) et l’intensité de pesanteur en
newtons par kilogramme (N.kg–1)
3.2 – Poids et force d’attraction gravitationnelle
La chute de la pomme inspire à Newton une réflexion révolutionnaire pour l’époque : les lois qui
régissent le monde terrestre doivent être les mêmes que celles qui régissent les cieux.
Ainsi, l’action mécanique qui explique la chute d’un objet (modélisée par le poids de l’objet) et
l’action mécanique qui explique que la Lune gravite autour de la Terre (modélisée par la force
d’attraction gravitationnelle) constituent une seule et même action mécanique.
Si la Lune ne tombe pas sur la Terre, c’est qu’elle possède une vitesse suffisante.
« Il fallait être Newton pour apercevoir que la Lune tombe, alors que tout le monde voit bien qu’elle
ne tombe pas. » Paul Valéry, Mélange (1934).