ANNEXE RADIOCHRONOLOGIE ELEVE.pages

!
Pour déterminer l'âge d'un échantillon, il faut définir l'instant 0 de sa formation. La mesure du temps qui nous sépare de sa
formation est réalisée en utilisant un chronomètre dont le principe repose sur la désintégration d'éléments radioactifs
(atomes) instables composant un minéral ou un fossile. La datation absolue détermine l'âge des minéraux, des roches et
des fossiles. Elle s'exprime, généralement, en milliers ou millions d’années (Ma).
Comment la désintégration d’atomes radioactifs permet-elle d'établir une datation absolue ?
Qu’est ce que c’est ?
!
datation radiométrique = par radiochronologie ! = méthode de datation absolue utilisant la variation régulière au cours du
temps de la proportion de (radio)isotopes dans certains corps
!
A quoi çà sert ?
!
-1/ obtenir des estimations quantitatives de l'âge des événements géologiques, basée sur le principe de la
désintégration radioactive
-2/ à dater une roche donc reconstituer l’histoire de la Vie et de la Terre par la désintégration suivant des lois avec
équations mathématiques exponentielles permettant de dater un minéral donc une roche la contenant et donc un fossile
dedans ou l’âge de la couche où est cette roche qui est de même âge. Cette technique peut se coupler au principe de la
datation relative pour estimer un âge
!
Exemples
!
-datation de l’âge de la Terre
-datation de Toumaï, notre plus ancien ancêtre la ligné humaine (1A4 : Un regard sur l’Homme), découvert par l’équipe
de Michel Brunet en 2004 au Nord du Tchad (signifie espoir de Vie en Goran)
-établissement des échelles de temps géologiques
-datation d’un morceau de bois (xylème II : partie 1A5 du programme)
!
1/ principe
!
piégés dans les minéraux de ces roches à leur formation, formant dès lors un système clos, le minéral en question
n’échange plus avec son environnement chimiquement (ni apport ni perte de l’isotope). Dès lors, on s’appuie sur des
prévisions graphiques algébriques mathématiques exponentielles de la dégradation temporelle de cet isotope en un autre
au cours du temps (accès possible donc à la vitesse de décroissance). Au sein du dit minéral : l’isotope radioactif
( = isotope père P) émet un rayonnement particulier (variable selon l’élément) pour donner un isotope stable ( = élément
fils F) :
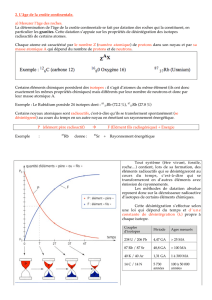
Ainsi, le temps passant, le nombre d’atomes de l’isotope père P décroît et celui de l’isotope fils F croît.
Toutes les méthodes de datation absolue reposent sur la possibilité de mesure de ces 2 concentrations P et F à un instant t
sachant (ou pas) P0 et F0 à t = 0; fermeture du système.Tout ceci n’étant valable évidemment que si et seulement si le
système est clos.
!
Les lois de la désintégration - Équations fondamentales de la géochronologie
!
Les méthodes de la géochronologie reposent sur le principe suivant :
!
Soit un isotope radioactif Père (P) qui se désintègre en élément radiogénique fils (F) : P ---------> F
Le rapport de concentration P/F à un instant donné est une fonction de la constante de désintégration λ (qui est la
probabilité de désintégration par unité de temps) de l'élément P et de l'âge t. La quantité d'atomes P désintégrés dans le
temps dt est proportionnelle au nombre P d'atomes et à la constante de désintégration λ. On peut alors écrire :
Chapitre 1
!
LE DOMAINE CONTINENTAL : GENESE ET CARACTERISATION :
DETERMINATION DE L’AGE D’UNE ROCHE PAR RADIOCHRONOLOGIE
1

P = nombre d'atomes pères radioactifs
λ = constante de désintégration
dP/dt = taux instantané de transformation
!
Si P0 représente la quantité d'atomes pères à l'instant t0, l'équation 1 s'intègre selon les équations (2) et (3) :
Dans la pratique, on ne doit faire intervenir dans l'équation que des grandeurs mesurables actuellement. Or, on ne connaît
pas le nombre d'atomes pères P0 à l'instant initial t0. Au cours du temps, un certain nombre d'atomes P0 radioactifs se
sont transformés en éléments fils F. On pose alors l'hypothèse, que le nombre d'atomes père à un temps t (P) est égal au
nombre d'atomes pères initiaux (t0) moins le nombre d'atomes fils F produits au cours du temps t. Soit :
P = P0 - F ou P0 = P + F
En remplaçant P0 par sa valeur (P + F) dans l'équation (3) on obtient :
P + F = P e^λt ou F = P e^λt - P ; soit :
De cette équation (4) on peut en déduire l'âge (t) :
Un problème peut apparaître. La quantité d'atomes F mesurés aujourd'hui correspond en fait à la quantité d'atomes fils
provenant de la désintégration de l'élément père (P) radioactif, mais aussi à la quantité d'atomes fils (F0) qui étaient
présents dès le départ dans le système. C'est à dire que :
F total mesuré = F formé à t=t + F0
L'équation (4) peut alors s'écrire :
Cette équation (6) est l'équation fondamentale de la géochronologie.
Elle permet d'obtenir l'âge d'une formation (ou d'un minéral) selon l'équation (7)
2

L'âge est obtenu dans les conditions suivantes :
1. la constante de désintégration λ soit connue avec précision
2. que l'on connaisse P et F avec une bonne précision
3. que l'on connaisse F0 ; ce qui est souvent délicat, voir impossible
4. que le système soit resté clos: “Rien ne se perd, rien ne se crée, tout se transforme”
!
2/ l’exemple-application en TS : la méthode Rb/Sr
!
L’isotope radioactif père P 87 Rb présent dans des minéraux des granites et gneiss, micas et feldspaths se désintègre au
cours du temps pour donner l’élément fils F 87 Sr stable : dans chaque minéral du système, au cours du temps, la quantité
de 87 Rb décroît et celle de 87 Sr croît suivant les lois de la radioactivité.
!
A la formation de la roche, 87 Rb a été emprisonné mais aussi 87 Sr : donc 87 Sr (t )= 87 Sr (0) + 87 Sr formé depuis la
désintégration de 87 Rb : les teneurs initiales étant inconnues, on a besoin de plusieurs minéraux et non un pour
déterminer l’âge de la roche. On utilise aussi l’isotope stable 86 Sr incorporé comme le 87 Sr lors de la formation de la
roche mais son taux est constant donc
87 Sr/ 86 Sr était le même dans tous
les minéraux à la fermeture du système
(comme dans le magma d’origine)
mais 87 Sr/ 86 Sr étaient différents.
!
à t = t (0) : solidification du magma
(fermeture du système) : les 3
minéraux de la roche = à 87 Sr/ 86 Sr
identiques mais 87 Rb / 86 Sr
différents.
!
à t = t : 87 Rb/ 86 Sr diminue et 87 Sr /
86 Sr augmente car 87 Rb se
désintègre en 87 Sr à raison de 1 pour
1.
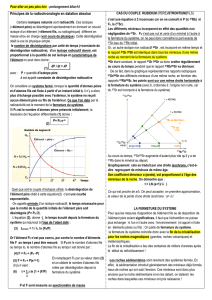
Ainsi, à partir des mesures à t = actuel
des taux, on obtient une droite appelée
isochrone de pente indiquant le temps
écoulé depuis la formation de ces 3
minéraux et donc l’âge de la roche.
!
quand a : âge et quand a ↘ :
âge ↘
!
Principe & équation fondamentale
!
Le Rb37 possède 2 isotopes : 85Rb et
87Rb. Le 87Rb est radioactif et se
désintègre par radioactivité ß en 87Sr
radiogénique. 87Rb ------>87Sr (radioactivité ß)
Selon l’équation fondamentale de désintégration (6) du 87Rb (éléments père radioactif, P) en 87Sr (élément fils
radiogénique, F) : (6) F = P (eλt - 1) + F0
On peut écrire : (8) (87Sr) = (87Rb) (e λt - 1) + (87Sr )0
λ = 1,42.10-11an-1
3

Sr38 possède 4 isotopes 84-86-87-88. Seul 87Sr est radiogénique. Dans l'équation (8), (87Sr), (87Rb) peuvent être
mesurés et sont connus. Par contre la quantité de (87Sr)0 est une inconnue. Le 86Sr est un isotope stable non radiogénique,
non radioactif. Sa quantité dans le système est donc une constante. Dans l'équation (8), on rapporte les concentrations de
(87Sr)t, (87Rb)t et (87Sr)0 à cet isotope stable (86Sr).
 Cette équation est de la forme y = ax + b
Considérons plusieurs échantillons cogénétiques de même âge, distincts des uns des autres par leur rapport 87Rb/86Sr,
évoluant en système clos ; les points représentatifs de ces échantillons doivent dans un diagramme (87Sr/86Sr) - (87Rb/86Sr)
s'aligner sur une droite, dénommée isochrone, dont la pente (eλt-1) est fonction de l'âge du système. L'ordonnée à l'origine
permet de connaître le rapport (87Sr/86Sr)0(fig.1) (fig.2). La croûte océanique a un âge compris entre 0 (genèse actuelle aux
dorsales, voir II/) et 200 Ma.
Comment le détermine t-on ? 1ère S : rappel : par les anomalies magnétiques et la connaissance de V accrétion dans les
fonds
!
Pour la croûte continentale, nous allons chercher à déterminer son âge et la fourchette équivalente parmi celles trouvées
sur Terre.
!
Comment la détermine t-on ? par radiochronologie !
http://www.biopathe.fr/file/videos/radiochrono/radiochronologie%20rb%20sr%20WMVHD720.wmv
https://www.youtube.com/watch?v=_lQcRk-Lfxg
http://www.cnrs.fr/cnrs-images/sciencesdelaterreaulycee/contenu/geochrono2.htm
http://svt.ac-amiens.fr/archives_svt/info/logiciels/radiochr/index.htm
!
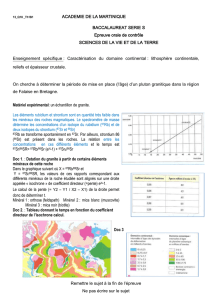
A savoir pour le Bac : la pente a de la droite isochrone a pour formule a = e^(⋋t)-1
Au Bac, on ne vous demande pas de résoudre cette équation exponentielle, mais de mettre en relation le temps écoulé et
ce coefficient directeur a (pente de la droite) qui sera à calculer puis utiliser le tableau pour déterminer l’âge de la roche
!
Logiciel TS dédié :
!
http://svt.ac-amiens.fr/archives_svt/info/logiciels/radiochr/index.htm
http://svt.ac-amiens.fr/archives_svt/info/logiciels/radiochr/telech.htm
http://florimont.info/message-3-370-un-qcm-sur-la-datation-absolue.html
!
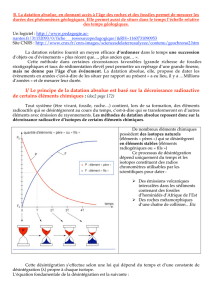
Le logiciel radiochronologie présente un modèle de décroissance de la quantité d’éléments radioactifs et donne
des exemples de datation en rapport avec le programme de Tale S
4