TP Échantillonnage – Conversion analogique numérique

Électronique
PSI
A. Lesage
1
Lycée Vaucanson (Tours)
TP Échantillonnage  Conversion analogique
numérique
I. Intérêt de la conversion analogique  numérique
II.1. Principe
II.2. Filtre anti repliement
II.3. Mouvement apparent d’un segment tournant
III.1. Présentation du montage
III.2. Échantillonneur simple
III.3. Échantillonneur bloqueur
-
forme Sysam-SP5
IV.1. Échantillonnage
IV.2. Codage des valeurs quantifiées
V. Annexe 
 :
http://www-igm.univ-
mlv.fr/~dr/XPOSE2005/JavaSound_arinie/general/echantillonage.html
 :
http://www.ostralo.net/3_animations/swf/echantillonnage.swf
 :
http://culturesciencesphysique.ens-lyon.fr/ressource/principe-numerisation.xml
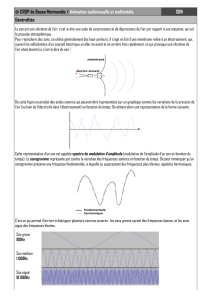
I. 
électromagnétique, température, etc.) on utilise en général un capteur dont le rôle est de
convertir le signal physique en un signal électrique qui est donc une fonction continue
du temps (au sens mathématique) image des variations temporelles de la grandeur
physique étudiée. Ce type de signal est qualifié d'analogique par opposition à un signal
numérique.

Électronique
PSI
A. Lesage
2
Lycée Vaucanson (Tours)
signal vis-à-vis du bruit électronique, création de copies parfaites, traitement facilité par
un calculateur, miniaturisation etc.). L'opération de numérisation correspond à la
succession de 3 étapes schématisées Figure 1 :
 l’échantillonnage (sampling en anglais) qui permet de prélever un ensemble de
valeurs (appelées échantillons) prises à des instants discrets ;
 la quantification qui alloue à chacun de ces échantillons une valeur approchée (et
qui correspond à une discrétisation des valeurs du signal) ;
 le codage qui consiste à coder en binaire sur un nombre fini de bits chaque niveau
quantifié.
000
001
010
011
100
101
110
111
000
001
010
011
100
101
110
111
Codage
Quantification
Échantillonnage

Électronique
PSI
A. Lesage
3
Lycée Vaucanson (Tours)
Figure 1 : Échantillonnage, quantification et codage d’un signal
On a supposé ici une quantification par valeur inférieure.
À noter que la quantification du signal sur la Figure 1  sur 8 niveaux ce qui
correspond à 3 bits.
II. 
II.1. Principe
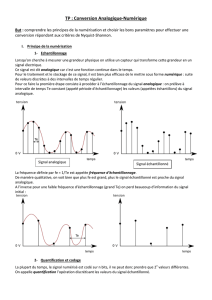
Échantillonner un signal consiste à prendre un certain nombre de points régulièrement
espacés de ce signal. Mathématiquement cette opération revient à multiplier le signal
analogique original  par un signal  d'amplitude 1 à chaque instant pour lequel
on prend un échantillon (opération répétée à la période ) et d'amplitude zéro sinon.
Cette fonction est appelée peigne de Dirac.
Signal analogique
Signal échantillonné
Peigne de Dirac
 correspond donc au
nombre de valeurs prélevées par seconde.
000
001
010
011
100
101
110
111
Codage
Quantification
Échantillonnage
Signal numérisé
1

Électronique
PSI
A. Lesage
4
Lycée Vaucanson (Tours)
Influence de la fréquence d’échantillonnage
http://www.ostralo.net/3_animations/swf/echantillonnage.swf
On comprend sur cette simulation que pour que la reconstruction du signal de sortie soit
fidèle au signal d'entrée  suffisamment grande.
En effet, si celle-ci est trop faible, les variations rapides du signal ne pourront être
retranscrites.         donnera une quantité
Le critère de Nyquist-Shannon introduit le concept d'une fréquence d'échantillonnage
suffisante pour une reconstruction (à peu près !) 
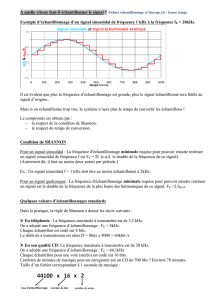
La simulation fait apparaître que  doit être supérieure à deux fois la fréquence du
signal sinusoïdal utilisé.
différents pour une fréquence  donnée. On a représentée ci-dessous deux sinusoïdes
de fréquence    (donc de période 10 s) et   échantillonnées à
  :
Figure 2
On constate que le signal échantillonné est identique pour les deux sinusoïdes. On parle
de phénomène d’aliasing en anglais (et de repliement de spectre en français). Par
référence au terme anglophone, on peut dire que  est alias de  par échantillonnage.
Sous-jacent on a ici le fait que   
Application n°
1.
Spectre d’un signal échantillonné
 peut être modélisé par la multiplication
de  par un signal    
 1.
Le signal  peut être décomposé en série de Fourier sous la forme :
avec  
 . On se placera dans le cas simple où  est suffisamment petit pour
que 
  . On a alors :
0
2

Électronique
PSI
A. Lesage
5
Lycée Vaucanson (Tours)
1. Soit   le signal analogique à échantillonner. Déterminer le
-ci pour   
. Par
quel type de filtrage peut-on récupérer le signal analogique de départ ?
Le signal à échantillonner contient cette fois deux sinusoïdes de fréquences  et  telles
que 
 :
Remarques
On aurait pu aussi écrire     mais cette écriture ne met pas en évidence le
caractère symétrique de  et  par rapport à 
.
2.         signal échantillonné en se
restreignant aux harmoniques    et   . Est-il possible de récupérer par
filtrage le signal analogique de départ ?
On considère cette fois-ci un signal  dont les fréquences des harmoniques utiles sont
comprises entre  et  :
3. Déterminer le spectre du signal échantillonné et représenter -ci en
distinguant les cas  
 et   .
Solution : Spectre d’un signal échantillonné
1. Le signal échantillonné est donné par :
avec 
 . On obtient alors le spectre :
0
0