Document de Synthèse

Document de Synthèse
Sujet de thèse:
Preuves formelles des programmes numériques en
prenant en compte l’architecture et le
compilateur
Thi Minh Tuyen NGUYEN
1 Objectifs et contributions
Sur des architectures récentes, un programme numérique peut donner des
réponses diférentes. La raison est qu’il existe des incohérences entre des exécu-
tions du programme sur des matériels différents. Précisément, la norme IEEE-
754 – une norme pour la représentation des nombres en virgule flottante, sup-
porté par la plupart des matériels – spécifie qu’un nombre flottant en double
précision est arrondi en 64 bits. Par contre, l’unité de calcul en virgule flottante
x87 (x87 FPU)– supportée par des processeurs de l’architecture IA32 – utilise
des registres en 80 bits. L’instruction FMA (fused multiply-add) – utilisée dans
les architectures PowerPC et Intel Itanium – calcule x×y±zavec un seul
arrondi. En outre, l’optimisation peut causer des incohérences du résultat.
Le but de cette thèse est de prouver formellement un programme numérique
en prenant en compte l’architecture et le compilateur. Pour le faire, nous avons
proposé deux approches différentes:
•Une approche permet de prouver des propriétés des programmes en virgule
flottante qui sont vraies sur plusieurs architectures et compilateurs. Cette
approche ne considère que les erreurs d’arrondi qui doivent être validées
quels que soient l’environnement matériel et le choix du compilateur.
•La deuxième approche consiste à prouver des propriétés des programmes
en analysant leur code assembleur. Nous nous concentrons sur des prob-
lèmes et des pièges qui apparaissent sur des calculs en virgule flottante.
L’analyse directe du code assembleur nous permet de considérer des
caratéristiques dépendant de l’architecture ou du compilateur telle que
l’utilisation des registres en précision étendue.
1

2 Preuves formelles de programmes numériques
indépendant de l’environment
2.1 Borne pour une opération en virgule flottante
Le choix entre l’arrondi en 64 bits, en 80 bits et en double arrondi est la rai-
son principale qui provoque l’incohérences du résultat. Nous prouvons une
borne d’erreur d’arrondi qui est valide quels que soient le matériel et l’arrondi
choisi. Nous désignons par ◦64(x)l’arrondi au plus proche en 64 bits, par
◦80(x)l’arrondi au plus proche en 80 bits, par ◦64(◦80 (x)) le double arrondi.
Le théorème suivant est la base de notre approche pour prouver correctement
des programmes numériques quels que soient l’architecture et le compilateur:
Theorem 1 Soit un nombre réel x, soit (x)défini par ◦64(x), ou ◦80(x), ou
le double arrondi ◦64(◦80(x)). Alors,
Si |x| ≥ 2−1022 alors 
x−(x)
x
≤2050 ×2−64 et |(x)| ≥ 2−1022
Si |x| ≤ 2−1022 alors !|x−(x)| ≤ 2049 ×2−1086 et |(x)| ≤ 2−1022
2.2 Preuve de programme numérique
2.2.1 FMA
Considérons que nous avons (x) = x. Un FMA est alors ((a×x) + b)avec
le intérieur qui est l’arrondi identité. Le théorème 1 est donc valide avec le
FMA.
2.2.2 Borne d’une séquence des opérations
Theorem 2 Soit une opération parmi addition, soustraction, multiplication,
division, racine carrée, négation et valeur absolue. Soit x=(y, z)le résultat
exact de cette opération (sans arrondi). Alors, quelle que soit l’architecture et
la compilation, le résultat calculé ˜xest
Si |x| ≥ 2−1022, alors
˜x∈x−2050 ×2−64 × |x|, x + 2050 ×2−64 × |x|\−2−1022 ,2−1022.
Si |x| ≤ 2−1022, alors
˜x∈x−2049 ×2−1086 , x + 2049 ×2−1086∩−2−1022 ,2−1022.
Theorem 3 Si nous considérons les formules du théorème 1 sur chaque opéra-
tion (addition, soustraction, multiplication, division, racine carrée, négation,
valeur absolue), l’erreur d’arrondi finale est correcte quelle que soit l’architecture
et la compilation, à condition que le compilateur respecte l’ordre des opérations.
2

2.3 Quand le compilateur réorganise des additions
Theorem 4 Soit nun entier tel que n≤1
ε, soit (ai)0≤i≤nune séquence des
nombres réels et Iun réel. Supposons que nous mettons dans la post-condition:
x⊕yest un nombre réel rtel que
|r−(x+y)| ≤ εn·(|x|+|y|) + n·η.
et pour un ordre o1des additions, nous pouvons déduire que |So1
n−Pn
0ai| ≤ I.
Maintenant si nous mettons dans la post-condition: x⊕yest un nombre réel
rtel que
|r−(x+y)| ≤ ε· |x+y|+η.
Alors, quel que soit l’ordre o2des additions, nous avons |So2
n−Pn
0ai| ≤ I.
2.4 Implémentation
Cette approche est implantée dans la plate-forme Frama-C pour l’analyse sta-
tique de code C.
Un point intéressant du plug-in Jessie est que nous pouvons changer
l’interprétation des opérations en virgule flottante facilement. Nous définissons
deux “pragmas” dite multirounding(multiroundingR dans le cas le compilateur
réorganise des additions) et changeons les post-conditions des opérations flot-
tantes (addition, soustraction, multiplication, division, racine carrée, négation
et valeur absolue) et nous mettons les formules du théorème 1 (théorème 4) à
la place pour chercher l’erreur d’arrondi de l’ensemble du programme.
3 Preuve formelle de programme numérique
dépendant de l’architecture et le compilateur
3.1 Vue générale
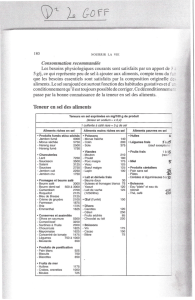
Notre approche permet de prover un programme C en analysant son code assem-
bleur. Pour le faire, il faut suivre les étapes illustrées dans la Figure 1. Toutes
les étapes nécessaires pour prouver un programme avec son code assembleur
sont présentées dans la figure à gauche. La figure à droite instancie ces étapes
pour la preuve d’un programme foo.c.
Dans un programme C annoté par ACSL (ANSI/ISO C Specification Lan-
guage), toutes les annotations sont mises dans les commentaires. Quand gcc
génère le code assembleur, ces annotations seront ignorées. Car les annotations
sont importantes pour prouver un programme, une étape de préparation est
donc nécessaire. Cette étape met toutes les annotations sous forme assembleur
inline pour que ces annotations apparaîssent dans le code assembleur généré.
Cette étape est implantée par la réalisation d’un traducteur.
Une fois que l’étape de préparation est fait, un autre fichier C contenant
assembleur inline est généré. En suite, nous utilisons gcc -S pour générer le
code assembleur à partir de ce fichier.
3

La traduction du code assembleur vers Why est implantée dans notre version
modifiée de GAS (GNU Assembler). Cette étape génère un fichier contenant les
obligations de preuve dans Why. Puis, ces obligations de preuve sont tentées de
prouver par des prouveurs automatiques/interactifs.
Progamme en C
+ annotations en ACSL
Programme en C
+ assembleur inline
Code assembleur
Obligations de preuve en Why
Prouvers automatiques
/prouvers interactifs
préparation de code
compilation de C
assembleur modifié
preuve
foo.c
foo_inline.c
foo_inline.s
foo_inline.why
Prouvers automatiques
/prouvers interactifs
./inlineasm foo.c
gcc -S foo_inline.c
./as-new foo_inline.s
gwhy foo_inline.why
Figure 1: Étapes pour traduire un programme C vers Why
3.2 Traduction vers Why
3.2.1 Modèle de données
Entier machine et nombres en virgule flottante La logique Why n’a
que des entiers et des réels non bornés. Nous réutilisons le modèle des entiers
machines fournis par le plug-in Jessie de Frama-C. Voici le modèle des entiers
en 32 bits. Celui en 64 bits est fait de la même façon.
type int32
logic integer_of_int32: int32 -> int
predicate is_int32(x:int) = -2147483648 <= x and x <= 2147483647
axiom int32_coerce: forall x:int32. is_int32(integer_of_int32(x))
Le type abstrait int32 pour les entiers en 32 bits est déclaré, avec une
fonction integer_of_int32 retournant la valeur qu’un entier machine désigne.
Le prédicat is_int32 vérifie si un entier se situe dans l’intervalle d’un entier en
4

32 bits, et nous posons un axiome pour spécifier que la valeur désignée par un
int32 est toujours dans cet intervalle.
Afin de représenter des nombres flottants, nous réutilisons le modèle des
nombres flottants en 32 et en 64 bits qui est défini par Ayad and Marché [1].
Ce modèle introduit les types abstraits single and double. Nous pouvons
également représenter le type binary80 pour un nombre flottant en 80 bits.
Voici le modèle pour les nombres flottants en 64 bits:
type mode = nearest_even | to_zero | up | down | nearest_away
type double
logic double_value : double -> real
logic round_double : mode, real -> real
predicate no_overflow_double(m:mode,x:real) =
abs(round_double(m,x)) <= 0x1.FFFFFFFFFFFFFp1023
Un type énuméré mode est défini pour cinq modes possibles d’arrondi. Le
type abstrait double pour les nombres flottants en 64 bits est déclaré, avec une
fonction double_value retournant la valeur réelle qu’il désigne. La fonction
logique round_double(m, x)retourne le nombre représentable en 64 bits après
avoir arrondi avec le mode m. Le prédicat no_overflow_double(m, x) vérifie
si un réel xarrondi en 64 bits avec le mode mest débordé.
Registres Une caractéristique importante de notre approche est comment
modéliser les registres que les instructions assembleurs utilisent. Le problème
est qu’un registre n’enregistre qu’une séquence des bits, qui peut être interpreter
comme un entier, un nombre flottant ou une adresse mémoire. En plus, nous
considérons qu’il n’y a pas de différence entre un registre en 64 bits et sa valeur
en 32 bits enregistrée dans la partie inférieure. Par exemple: il n’y a pas de
différence entre les registres rax et eax dans l’architecture x86.
Pour modéliser cet comportement, nous introduisons un type abstrait
register équipé avec quelques symboles d’accessibilité. Chaque symbole
désigne une “vue” différente de la valeur enregistrée dans le registre. Par exem-
ple, afin de modéliser \exact, le symbole sel_exact est la vue pour le calcul
avec la précision illimitée.
type register
logic sel_int32 : register -> int32
logic sel_int64 : register -> int64
logic sel_single : register -> single
logic sel_double : register -> double
logic sel_80 : register -> binary80
logic sel_exact : register -> real
Pour chaque registre, nous introduisons une variable Why avec le type
register.
5