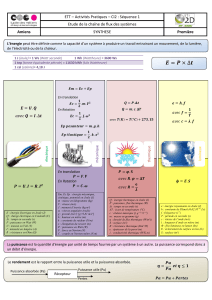
Module 1 - Résistance interne, pertes par effet Joule et perte en ligne.

MODULE 1.
Résistance interne (générateur).
Pertes par effet Joule.
Pertes en ligne.
Performances-seuils.
L’élève sera capable …
1. d’expliquer l’effet qu’occasionne la résistance interne d’une source de tension
et de calculer le taux de régulation ;
2. d’expliquer les pertes en ligne ;
3. d’expliquer les pertes par effet Joule.
MODULE 1 Résistance interne, pertes par effet Joule et perte en ligne.

1. Résistance interne des sources de tension
1.1. Résistance interne.
Toute source de force électromotrice, qu’il s’agisse d’une génératrice, d’une batterie ou d’une
alimentation de laboratoire (figure ci-dessous), à une certaine résistance interne.
Le circuit équivalent réel d’une source de f.é.m. est donc semblable à celui-ci :
Nous allons donc étudier l’incidence de la résistance interne d’une source sur sa tension de
sortie, de sorte que nous serons en mesure d’expliquer tout problème pouvant se présenter au
sujet d’une source de f.é.m.
Jusqu’à maintenant, notre analyse des circuits s’est faite avec l’hypothèse que la source de
tension employée était idéale, c’est-à-dire que sa résistance interne était nulle. Dorénavant,
nous tiendrons compte, sauf indication contraire, de l’existence de la résistance interne.
MODULE 1 Résistance interne, pertes par effet Joule et perte en ligne.

La source de tension idéale illustrée à la figure A, a une résistance interne nulle ; sa tension de
sortie E est constante, sans charge (SC) ou à pleine charge. Compte tenu maintenant de la
résistance interne de la source (figure B), la tension de sortie est E seulement si la charge est
nulle (Ic = 0). Dès qu'une charge (Rc) est raccordée à la source (figure C), la tension de sortie
de la source chute à Es, en raison de la chute de potentiel aux bornes de la résistance interne.
(Figure A) (Figure B)
(Figure C)
Appliquons la loi des tensions du circuit de la figure C, nous obtenons :
0
int =-´- S
ERIE
SC
EE =
0
int =-´- SSC ERIE
int
RIEE SCS ´-=
MODULE 1 Résistance interne, pertes par effet Joule et perte en ligne.

Cette dernière équation permet donc de calculer la résistance interne d'une source si elle est
inconnue En effet, on obtient par simple transformation:
I
E
I
E
I
EE
RSSCSSC ==
-
=
int
C
SC R
I
E
R-=
int
Conclusion:
Il suffit de mesurer la tension de sortie en l'absence de charge, et l'intensité du courant qui
passe dans le circuit de charge pour déterminer la valeur de la résistance interne de la source
utilisée.
Le dessin suivant représente un exemple de la courbe de tension de sortie en fonction de
l'appel de courant.
Remarquer que l'augmentation du courant de charge fait nécessairement augmenter le courant
qui passe dans la source et par conséquent, la chute de tension due à sa résistance interne, ce
qui provoque une baisse de la tension présente aux bornes de la source.
MODULE 1 Résistance interne, pertes par effet Joule et perte en ligne.

1.2 . Régulation de tension.
Idéalement, une source de tension fournirait une tension de sortie constante malgré les
variations du courant dans la charge (Ic). En d'autres termes, une source de 12V fournirait
constamment une tension de sortie de 12V malgré les variations de l'appel de courant dans la
charge. Toutefois, les sources de tensions réelles s'écartent de ces conditions idéales. Le taux
de régulation d'une source est une mesure de cet écart: il se définît à partir de la tension
fournie pour la charge maximale de service et de la tension fournie pour une charge nulle de la
façon suivante:
Taux de régulation (VR%) =
%100´
-
cm
cmcnEEE
Dans les conditions idéales, Ecm = Ecn et VR% = 0.
Par conséquent, plus petit est le taux de régulation et plus petite
est la variation de la tension de sortie avec la charge.
Il est également possible de démontrer que le taux de régulation est lui aussi donné par:
%100% int ´=
c
R
R
VR
Pour une charge donnée, plus petite est la résistance interne, plus petit est par conséquent le
taux de régulation.
2 . Pertes par effet Joule.
Lorsqu'un courant électrique circule dans un conducteur, on observe une augmentation de la
température de ce conducteur: cet effet est appelé « effet Joule ». Il est dû à la collision des
électrons avec les atomes du corps conducteur, qui libère ainsi de l'énergie sous forme de
chaleur. La puissance P dissipée par effet Joule, qui s'exprime en watts (symbole W), se
calcule par la relation: P=R.I2.
MODULE 1 Résistance interne, pertes par effet Joule et perte en ligne.